目录
- 1、信息熵 (information entropy)
- 2、条件熵 (Conditional entropy)
- 3、相对熵 (Relative entropy)
- 4、交叉熵 (Cross entropy)
- 5、 岭回归(Ridge Regression)
- 6、什么是概率分布?
- 7、反向传播算法推导
- 8、梯度下降法
- 9、凸优化
- 10、无偏估计
- 11、 为什么方差的分母是 n − 1 n-1 n−1 ?
- 12、协方差矩阵
- 13、流形学习概述
- 14、关于感受野的总结
- 15、深度学习中Embedding层有什么用?
- 16、GAN
- 17、图神经网络和传统图模型,以及深度学习间的关系
- 17、[什么是零样本学习?](https://www.analyticsindiamag.com/what-is-zero-shot-learning/)
- 18、attention机制
1、信息熵 (information entropy)
熵 (entropy) 一词最初来源于热力学。1948年,香农将热力学中的熵引入信息论,所以也称香农熵 (Shannon entropy) 或信息熵 (information entropy)。本文只讨论信息熵。首先,我们来理解一下信息这个概念。信息是一个很抽象的概念,百度百科将它定义为:指音讯、消息、通讯系统传输和处理的对象,泛指人类社会传播的一切内容。那么,信息可以被量化么?可以!香农提出的“信息熵”解决了这一问题。
一条信息的信息量大小和它的不确定性有直接的关系。我们需要搞清楚一件非常非常不确定的事,或者是我们一无所知的事,就需要了解大量的信息。相反,如果我们对某件事已经有了较多的了解,我们就不需要太多的信息就能把它搞清楚。所以,从这个角度,我们可以认为,信息量的度量就等于不确定性的多少。比如,有人说广东下雪了。对于这句话,我们是十分不确定的。因为广东几十年来下雪的次数寥寥无几。为了搞清楚,我们就要去看天气预报,新闻,询问在广东的朋友,而这就需要大量的信息,信息熵很高。再比如,中国男足进军2022年卡塔尔世界杯决赛圈。对于这句话,因为确定性很高,几乎不需要引入信息,信息熵很低。
考虑一个离散的随机变量 x x x,由上面两个例子可知,信息的量度应该依赖于概率分布 p ( x ) p(x) p(x),因此我们想要寻找一个函数 I ( x ) I(x) I(x),它是概率 p ( x ) p(x) p(x) 的单调函数,表达了信息的内容。怎么寻找呢?如果我们有两个不相关的事件 x x x 和 y y y,那么观察两个事件同时发生时获得的信息量应该等于观察到事件各自发生时获得的信息之和,即: I ( x , y ) = I ( x ) + I ( y ) I(x,y)=I(x)+I(y) I(x,y)=I(x)+I(y)。
因为两个事件是独立不相关的,因此 p ( x , y ) = p ( x ) p ( y ) p(x,y)=p(x)p(y) p(x,y)=p(x)p(y)。根据这两个关系,很容易看出 I ( x ) I(x) I(x)一定与 p ( x ) p(x) p(x)的对数有关(因为对数的运算法则是 log a ( m n ) = log a m + log a n \log_a{(mn)}=\log_a{m}+\log_a{n} loga(mn)=logam+logan)。因此,我们有 I ( x ) = − log p ( x ) I(x)=−\log{p(x)} I(x)=−logp(x),其中负号是用来保证信息量是正数或者零。而 log函数基的选择是任意的(信息论中基常常选择为2,因此信息的单位为比特bits;而机器学习中基常常选择为自然常数,因此单位常常被称为奈特nats)。 I ( x ) I(x) I(x)也被称为随机变量 x x x 的自信息 (self-information),描述的是随机变量的某个事件发生所带来的信息量。如图:
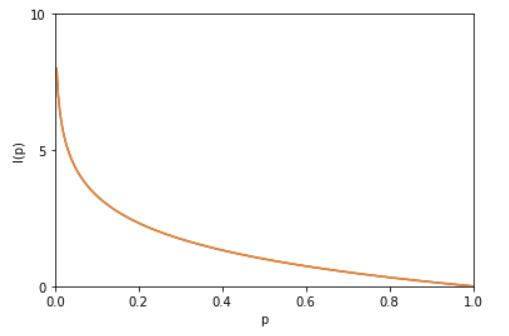
最后,我们正式引出信息熵。 现在假设一个发送者想传送一个随机变量的值给接收者。那么在这个过程中,他们传输的平均信息量可以通过求 I ( x ) = − log p ( x ) I(x)=−\log{p(x)} I(x)=−logp(x) 关于概率分布 p ( x ) p(x) p(x)的期望得到,即:
H ( X ) = − ∑ x p ( x ) log p ( x ) = − ∑ i = 1 n p ( x i ) log p ( x i ) H(X)=−\sum\limits_x{p(x)\log{p(x)}}=−\sum_{i=1}^n{p(x_i)\log{p(x_i)}} H(X)=−x∑p(x)logp(x)=−i=1∑np(xi)logp(xi)
H ( X ) H(X) H(X) 就被称为随机变量 x x x的熵,它是表示随机变量不确定的度量,是对所有可能发生的事件产生的信息量的期望。
从公式可得,随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大,且 0 ≤ H ( X ) ≤ log n 0≤H(X)≤\log{n} 0≤H(X)≤logn。稍后证明。将一维随机变量分布推广到多维随机变量分布,则其联合熵 (Joint entropy) 为:
H ( X , Y ) = − ∑ x , y p ( x , y ) log p ( x , y ) = − ∑ i = 1 n ∑ j = 1 m p ( x i , y i ) log p ( x i , y i ) H(X,Y)=−∑_{x,y}p(x,y)\log{p(x,y)}=−∑_{i=1}^{n}∑_{j=1}^{m}p(x_i,y_i)\log{p(x_i,y_i)} H(X,Y)=−x,y∑p(x,y)logp(x,y)=−i=1∑nj=1∑mp(xi,yi)logp(xi,yi)
注意点:
- 熵只依赖于随机变量的分布,与随机变量取值无关,也可以将 X X X的熵记作 H ( p ) H(p) H(p)。
- 令 0 log 0 = 0 0\log{0}=0 0log0=0(因为某个取值概率可能为0)。
那么,这些定义有什么样的性质呢?考虑一个随机变量 x x x。这个随机变量有4种可能的状态,每个状态都是等可能的。为了把 x x x 的值传给接收者,我们需要传输2比特的消息。
H ( X ) = − 4 × 1 4 × l o g 2 1 4 H(X)=−4×\frac{1}{4}×log_{2}{\frac{1}{4}} H(X)=−4×41×log241 = 2 bits
现在考虑一个具有4种可能的状态 {a,b,c,d}的随机变量,每个状态各自的概率为 (1/2,1/4,1/8,1/8)
这种情形下的熵为:
H ( X ) = − 1 / 2 log 2 1 / 2 − 1 / 4 log 2 1 / 4 − 1 / 8 log 2 1 / 8 − 1 / 8 log 2 1 / 8 H(X)=−1/2\log_2{1/2}−1/4\log_2{1/4}−1/8\log_2{1/8}−1/8\log_2{1/8} H(X)=−1/2log21/2−1/4log21/4−1/8log21/8−1/8log21/8=1.75 bits
我们可以看到,非均匀分布比均匀分布的熵要小。现在让我们考虑如何把变量状态的类别传递给接收者。与之前一样,我们可以使用一个2比特的数字来完成这件事情。然而,我们可以利用非均匀分布这个特点,使用更短的编码来描述更可能的事件,使用更长的编码来描述不太可能的事件。我们希望这样做能够得到一个更短的平均编码长度。我们可以使用下面的编码串(哈夫曼编码):0、10、110、111来表示状态 {a,b,c,d}。传输的编码的平均长度就是:
average code length = 1 2 × 1 + 1 4 × 2 + 2 × 1 8 × 3 \frac{1}{2}×1+\frac{1}{4}×2+2×\frac{1}{8}×3 21×1+41×2+2×81×3=1.75 bits
这个值与上方的随机变量的熵相等。熵和最短编码长度的这种关系是一种普遍的情形。
Shannon 编码定理 表明熵是传输一个随机变量状态值所需的比特位下界(最短平均编码长度)。因此,信息熵可以应用在数据压缩方面。这里讲的很详细。
证明0≤H(X)≤logn
利用拉格朗日乘子法证明:
因为 p(1)+p(2)+⋯+p(n)=1
所以有
目标函数:f(p(1),p(2),…,p(n))=−(p(1)logp(1)+p(2)logp(2)+⋯+p(n)logp(n))
约束条件:g(p(1),p(2),…,p(n),λ)=p(1)+p(2)+⋯+p(n)−1=0
1、定义拉格朗日函数:
L(p(1),p(2),…,p(n),λ)=−(p(1)logp(1)+p(2)logp(2)+⋯+p(n)logp(n))+λ(p(1)+p(2)+⋯+p(n)−1)
2、L(p(1),p(2),…,p(n),λ)
分别对 p(1),p(2),p(n),λ 求偏导数,令偏导数为 0
:
λ−log(e⋅p(1))=0
λ−log(e⋅p(2))=0
……
λ−log(e⋅p(n))=0
p(1)+p(2)+⋯+p(n)−1=0
3、求出 p(1),p(2),…,p(n)
的值:
解方程得,p(1)=p(2)=⋯=p(n)=1n
代入 f(p(1),p(2),…,p(n))
中得到目标函数的极值为 f(1n,1n,…,1n)=−(1nlog1n+1nlog1n+⋯+1nlog1n)=−log(1n)=logn
由此可证 logn
为最大值。
总结:
信息熵是衡量随机变量分布的混乱程度,是随机分布各事件发生的信息量的期望值。随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大;信息熵推广到多维领域,则可得到联合信息熵;条件熵表示的是在 X给定条件下,Y 的条件概率分布的熵对 X的期望。
- 信息熵是传输一个随机变量状态值所需的比特位下界(最短平均编码长度)。
1. 熵
熵:指的是一组样本的混乱度。
E n t r o p y ( S ) = ∑ i = 1 c − p i log p i Entropy(S) = \sum_{i=1}^{c} -p_i \log{p_i} Entropy(S)=i=1∑c−pilogpi
例子:
一个袋子里有50颗巧克力,50颗为红色。 熵为0表示没有随机性。
一个袋子里有50颗巧克力,25颗为红色,25颗为蓝色。 熵为1表示呈均匀分布。
一个袋子里有4中颜色,每种颜色个数相同。 熵为2,也表示均匀分布。
熵是和属性有关的,上面的熵为0,是说样本集在属性“颜色”上是纯的。
2、条件熵 (Conditional entropy)
条件熵 H(Y|X)表示在已知随机变量 X 的条件下随机变量 Y 的不确定性。条件熵 H(Y|X) 定义为 X 给定条件下 Y的条件概率分布的熵对X的数学期望:
条件熵 H(Y|X)相当于联合熵 H(X,Y) 减去单独的熵 H(X),即H(Y|X)=H(X,Y)−H(X),证明如下:
举个例子,比如环境温度是低还是高,和我穿短袖还是外套这两个事件可以组成联合概率分布 H(X,Y),因为两个事件加起来的信息量肯定是大于单一事件的信息量的。假设 H(X) 对应着今天环境温度的信息量,由于今天环境温度和今天我穿什么衣服这两个事件并不是独立分布的,所以在已知今天环境温度的情况下,我穿什么衣服的信息量或者说不确定性是被减少了。当已知 H(X) 这个信息量的时候,H(X,Y)剩下的信息量就是条件熵:
H(Y|X)=H(X,Y)−H(X)
因此,可以这样理解,描述 X和 Y 所需的信息是描述 X 自己所需的信息,加上给定 X 的条件下具体化 Y所需的额外信息。关于条件熵的例子可以看这篇文章,讲得很详细。
3、相对熵 (Relative entropy)
相对熵 (Relative entropy),也称KL散度 (Kullback–Leibler divergence)。设 p(x)、q(x) 是 离散随机变量 X 中取值的两个概率分布,则 p 对 q的相对熵是:
DKL(p||q)=∑xp(x)logp(x)q(x)=Ep(x)logp(x)q(x)
性质:
1、如果 p(x)
和 q(x)
两个分布相同,那么相对熵等于0
2、DKL(p||q)≠DKL(q||p)
,相对熵具有不对称性。大家可以举个简单例子算一下。
3、DKL(p||q)≥0
证明如下(利用Jensen不等式https://en.wikipedia.org/wiki/Jensen%27s_inequality):
因为:
∑xp(x)=1
所以:
DKL(p||q)≥0
总结:相对熵可以用来衡量两个概率分布之间的差异,上面公式的意义就是求 p
与 q 之间的对数差在 p
上的期望值。
相对熵可以用来衡量两个概率分布之间的差异。
- 相对熵是指用 q 来表示分布 p 额外需要的编码长度。
4、交叉熵 (Cross entropy)
现在有关于样本集的两个概率分布 p ( x ) p(x) p(x)和 q ( x ) q(x) q(x),其中 p ( x ) p(x) p(x) 为真实分布, q ( x ) q(x) q(x)为非真实分布。
用 p ( x ) p(x) p(x)来表示衡量识别一个样本所需要编码长度的期望(平均编码长度)为: H ( p ) = ∑ x p ( x ) l o g p ( x ) H(p)=∑_xp(x)logp(x) H(p)=x∑p(x)logp(x)
用 q ( x ) q(x) q(x)来表示 p ( x ) p(x) p(x)的平均编码长度,则是: H ( p , q ) = ∑ x p ( x ) l o g q ( x ) H(p,q)=∑_xp(x)logq(x) H(p,q)=x∑p(x)logq(x)
(因为用 q(x) 来编码的样本来自于分布 q(x) ,所以 H(p,q) 中的概率是 p(x))。此时就将 H(p,q) 称之为交叉熵。举个例子。考虑一个随机变量 x,真实分布p(x)=(12,14,18,18),非真实分布 q(x)=(14,14,14,14), 则H§=1.75 bits(最短平均码长),交叉熵 H(p,q)=12log24+14log24+18log24+18log24=2 bits。由此可以看出根据非真实分布 q(x) 得到的平均码长度大于根据真实分布 p(x)得到的平均码长。
我们再化简一下相对熵的公式。DKL(p||q)=∑xp(x)logp(x)q(x)=∑xp(x)logp(x)−p(x)logq(x)
有没有发现什么?
熵的公式 H ( p ) = − ∑ x p ( x ) log p ( x ) H(p)=−\sum\limits_{x}p(x)\log{p(x)} H(p)=−x∑p(x)logp(x)
交叉熵的公式 H ( p , q ) = ∑ x p ( x ) l o g 1 q ( x ) = − ∑ x p ( x ) l o g q ( x ) H(p,q)=∑xp(x)log1q(x)=−∑xp(x)logq(x) H(p,q)=∑xp(x)log1q(x)=−∑xp(x)logq(x)
所以有:
DKL(p||q)=H(p,q)−H§
(当用非真实分布 q(x) 得到的平均码长比真实分布 p(x)
得到的平均码长多出的比特数就是相对熵)
又因为 DKL(p||q)≥0
所以 H(p,q)≥H§
(当 p(x)=q(x)
时取等号,此时交叉熵等于信息熵)
并且当 H§
为常量时(注:在机器学习中,训练数据分布是固定的),最小化相对熵 DKL(p||q) 等价于最小化交叉熵 H(p,q)
也等价于最大化似然估计(具体参考Deep Learning 5.5)。
在机器学习中,我们希望在训练数据上模型学到的分布 P(model)
和真实数据的分布 P(real) 越接近越好,所以我们可以使其相对熵最小。但是我们没有真实数据的分布,所以只能希望模型学到的分布 P(model) 和训练数据的分布 P(train)
尽量相同。假设训练数据是从总体中独立同分布采样的,那么我们可以通过最小化训练数据的经验误差来降低模型的泛化误差。即:
希望学到的模型的分布和真实分布一致,P(model)≃P(real)
但是真实分布不可知,假设训练数据是从真实数据中独立同分布采样的,P(train)≃P(real)
因此,我们希望学到的模型分布至少和训练数据的分布一致,P(train)≃P(model)
根据之前的描述,最小化训练数据上的分布 P(train)
与最小化模型分布 P(model) 的差异等价于最小化相对熵,即 DKL(P(train)||P(model))。此时, P(train) 就是DKL(p||q) 中的 p,即真实分布,P(model) 就是 q。又因为训练数据的分布 p 是给定的,所以求 DKL(p||q) 等价于求 H(p,q)
。得证,交叉熵可以用来计算学习模型分布与训练分布之间的差异。交叉熵广泛用于逻辑回归的Sigmoid和Softmax函数中作为损失函数使用。这篇文章先不说了。
交叉熵可以来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
- 交叉熵是指用分布 q 来表示本来表示分布 p 的平均编码长度。
3、如何通俗的解释交叉熵与相对熵
4、可以用于计算代价?
5、交叉熵的百度百科解释
6、信息熵到底是什么
7、详解机器学习中的熵、条件熵、相对熵和交叉熵
5、 岭回归(Ridge Regression)
L ( w ) = ∣ ∣ y ˆ − y ∣ ∣ 2 2 L(w)=∣∣yˆ−y∣∣_2^2 L(w)=∣∣yˆ−y∣∣22是经验风险,在经验风险的基础上加上表示模型复杂度的正则化项(regularization)或者惩罚项(penalty term),即结构风险。所以,线性回归是经验风险最小化,岭回归是结构风险最小化。
岭回归其实就是在损失函数上加上 L2 正则,使得每个变量的权重不会太大。当某些特征权重比较大的时候,自变化变化一点点,就会导致因变量变化很大,使得方差变大,有过拟合风险。
此时损失函数变为:
L ( w ) = ∣ ∣ y ˆ − y ∣ ∣ 2 2 + λ ∣ ∣ w ∣ ∣ 2 2 = ∣ ∣ X w − y ∣ ∣ 2 2 + λ ∣ ∣ w ∣ ∣ 2 2 = ( X w − y ) T ( X w − y ) + λ w T w = w T X T X w − y T X w − w T X T y − y T y + λ w T w \begin{aligned} L(w) &=∣∣yˆ−y∣∣_2^2 + λ∣∣w∣∣_2^2 \\ &=∣∣Xw−y∣∣_2^2 + λ∣∣w∣∣_2^2 \\ &=(Xw−y)^T(Xw−y) + λw^Tw \\ &=w^TX^TXw-y^TXw-w^TX^Ty-yTy+λw^Tw \end{aligned} L(w)=∣∣yˆ−y∣∣22+λ∣∣w∣∣22=∣∣Xw−y∣∣22+λ∣∣w∣∣22=(Xw−y)T(Xw−y)+λwTw=wTXTXw−yTXw−wTXTy−yTy+λwTw
令
∂
L
(
x
)
∂
w
=
0
\frac{∂L(x)}{∂w} = 0
∂w∂L(x)=0,得
∂
L
(
w
)
∂
w
=
2
X
T
X
w
−
X
T
y
+
X
T
y
+
2
λ
w
=
0
\frac{∂L(w)}{∂w} = 2X^TXw-X^Ty+X^Ty+2λw = 0
∂w∂L(w)=2XTXw−XTy+XTy+2λw=0
x
=
(
X
T
X
+
λ
I
)
−
1
X
T
y
.
x=(X^TX+\lambda I)^{-1}X^Ty.
x=(XTX+λI)−1XTy.
岭回归公式推导
矩阵求导参考
d
(
x
T
A
x
)
d
x
=
(
A
+
A
T
)
x
\frac{d(x^TAx)}{dx}=(A+A^T)x
dxd(xTAx)=(A+AT)x
d
(
A
x
)
d
x
=
A
T
\frac{d(Ax)}{dx}=A^T
dxd(Ax)=AT
d
(
x
T
A
)
d
x
=
A
\frac{d(x^TA)}{dx}=A
dxd(xTA)=A
d
x
T
x
d
x
=
2
x
\frac{dx^Tx}{dx}=2x
dxdxTx=2x
- Ridge Regression [1]
L = ∣ ∣ X W − Y ∣ ∣ 2 + ∣ ∣ W ∣ ∣ 2 \mathcal {L} = ||XW-Y||^2 + ||W||^2 L=∣∣XW−Y∣∣2+∣∣W∣∣2
∂ L ∂ W = 2 X T ( X W − Y ) + 2 λ W = 2 [ ( X T X + λ ) W − X T Y ] = 0 \begin{aligned} \frac{\partial \mathcal{L}} {\partial W} &=2X^T(XW-Y)+2 \lambda W\\ &=2[(X^TX+\lambda)W - X^TY] \\ &=0 \end{aligned} ∂W∂L=2XT(XW−Y)+2λW=2[(XTX+λ)W−XTY]=0
( X T X + λ ) W − X T Y = 0 (X^TX+\lambda)W - X^TY = 0 (XTX+λ)W−XTY=0
( X T X + λ ) W = X T Y (X^TX+\lambda)W = X^TY (XTX+λ)W=XTY
W = ( X T X + λ ) − 1 X T Y W =(X^TX+\lambda)^{-1} X^TY W=(XTX+λ)−1XTY
- Ridge Regression [2]
L = ∣ ∣ W X − Y ∣ ∣ 2 + ∣ ∣ W ∣ ∣ 2 \mathcal{L} = ||WX - Y||^2 + ||W||^2 L=∣∣WX−Y∣∣2+∣∣W∣∣2
∂ L ∂ W = 2 ( W X − Y ) X T + 2 λ W = 2 [ W ( X X T + λ ) − Y X T ] = 0 \begin{aligned} \frac{\partial \mathcal{L}} {\partial W} &=2(WX-Y)X^T+2 \lambda W\\ &=2[W(XX^T+\lambda) - YX^T] \\ &=0 \end{aligned} ∂W∂L=2(WX−Y)XT+2λW=2[W(XXT+λ)−YXT]=0
W ( X X T + λ ) − Y X T = 0 W(XX^T+\lambda) - YX^T = 0 W(XXT+λ)−YXT=0
W ( X X T + λ ) = Y X T W(XX^T+\lambda) = YX^T W(XXT+λ)=YXT
W = Y X T ( X X T + λ ) − 1 W =YX^T(XX^T+\lambda)^{-1} W=YXT(XXT+λ)−1
6、什么是概率分布?
从统计到概率,入门者都能用Python试验的机器学习基础
一个事件发生的几率是多少?
如果我本来就可以计算理论概率,那我为什么还要用统计样本的数值特征,特别是均值和标准差?
7、反向传播算法推导
8、梯度下降法
9、凸优化
10、无偏估计
什么是无偏估计?
定义: 设 { X 1 , X 2 , … , X n } {\{X_1,X_2, \dots, X_n\}} {X1,X2,…,Xn}是总体的一个样本集合。不论总体服从什么分布,样本均值都是总体均值的无偏估计量。
这是书上的原话。这怎么可能?样本的均值不一定等于总体均值啊?大多数情况下就是不等啊?!
无偏估计:估计量的均值等于真实值,即具体每一次估计值可能大于真实值,也可能小于真实值,而不能总是大于或小于真实值(这就产生了系统误差)。
估计量评价的标准:
(1)无偏性,是指估计量不总是大于或小于真实值
(2)有效性,是指估计量与总体参数的离散程度。如果两个估计量都是无偏的,那么离散程度较小的估计量相对而言是较为有效的。即虽然每次估计都会大于或小于真实值,但是偏离的程度都更小的估计更优。
(3)一致性,又称相合性,是指随着样本容量的增大估计量愈来愈接近总体参数的真值。
无偏估计虽然在数学上更好,但是并不总是“最好”的估计,在实际中经常会使用具有其它重要性质的有偏估计。
举例:现在甲市有一万名小学三年级学生,他们进行了一次统考,考试成绩服从1~100的均匀分布:00001号学生得1分,00002号学生得1.01分……10000号学生得100分。那么他们的平均分是多少?(1+1.01+1.02+…+100)/10000=50.5,这个值叫做 总体平均数。
现在假定你是教委的一个基层人员,教委主任给你一个早上时间,让你估算一下全市学生的平均成绩,你怎么办?把全市一万名学生都问一遍再计算时间显然是来不及了,因此在有限的时间里,你找到了一个聪明的办法:给全市的78所小学每一所学校打了一个电话,让他们随机选取一名学生的成绩报上来,这样你就得到了78个学生的成绩,这78个学生就是你的**样本**。
你现在的任务很简单了,拿这78个学生的成绩相加并除以78,你就得到了样本平均数。你把这个数报告给教委主任,这个数就是你估算出来的全市平均成绩。
这个样本平均数会不会等于总体平均数50.5?很显然这和你的“手气”有关——不过大多数情况下是不会相等的。
那么问题来了:既然样本平均数不等于总体平均数(也就是说你报给教委主任的平均分和实际的平均分非常有可能是不一样的),要它还有用吗?有!因为样本平均数是总体平均数的无偏估计—— 也就是说只要你采用这种方法进行估算,估算的结果的期望值(你可以近似理解为很多次估算结果的平均数)既不会大于真实的平均数,也不会小于之。换句话说:你这种估算方法没有系统上的偏差 ,而产生误差的原因只有一个:随机因素(也就是你的手气好坏造成的)。
11、 为什么方差的分母是 n − 1 n-1 n−1 ?
结论: 这个问题本身概念混淆了。如果已知全部的数据,那么均值和方差可以直接求出。但是对一个随机变量 X X X,需要估计它的均值和方差,此时才用分母为 n − 1 n-1 n−1的公式来估计他的方差,因此分母是 n − 1 n-1 n−1才能使对方差的估计(而不是方差)是无偏的。因此,这个问题应该改为,为什么随机变量的方差的估计的分母是n-1?
如果我们已经知道了全部的数据,那就可以求出均值 μ μ μ,sigma,此时就是常规的分母为n的公式直接求,这并不是估计!
现在,对于一个随机变量X,我们要去估计它的期望和方差。
期望的估计就是样本的均值
x
ˉ
\bar{x}
xˉ
现在,在估计的X的方差的时候,如果我们预先知道真实的期望μ,那么根据方差的定义:
E [ ( X i − μ ) 2 ] = σ 2 E[(X_i-\mu)^2] = \sigma^2 E[(Xi−μ)2]=σ2
E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] = σ 2 E[\frac {1} {n} \sum\limits_{i=1}^n(X_i-\mu)^2] = \sigma^2 E[n1i=1∑n(Xi−μ)2]=σ2
这时分母为n的估计是正确的,就是无偏估计!
但是,在实际估计随机变量X的方差的时候,我们是不知道它的真实期望的,而是用期望的估计值
x
ˉ
\bar{x}
xˉ 去估计方差,那么:
1 n ∑ i = 1 n ( X i − X ˉ ) 2 = 1 n ∑ i = 1 n ( ( X i − μ ) + ( μ − X ˉ ) ) 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 + 2 n ∑ i = 1 n ( X i − μ ) ( μ − X ˉ ) + 1 n ∑ i = 1 n ( μ − X ˉ ) 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 + 2 ( X ˉ − μ ) ( μ − X ˉ ) + ( μ − X ˉ ) 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 − ( μ − X ˉ ) 2 \begin{aligned} \frac {1} {n} \sum\limits_{i=1}^n(X_i-\bar{X})^2 = &\frac {1} {n} \sum\limits_{i=1}^n((X_i-\mu)+(\mu-\bar{X}))^2\\ = &\frac {1} {n} \sum\limits_{i=1}^n(X_i-\mu)^2 + \frac {2} {n} \sum\limits_{i=1}^n(X_i-\mu)(\mu-\bar{X})+\frac {1} {n} \sum\limits_{i=1}^n(\mu-\bar{X})^2 \\ = &\frac {1} {n} \sum\limits_{i=1}^n(X_i-\mu)^2 + 2 (\bar{X}-\mu)(\mu-\bar{X})+(\mu-\bar{X})^2 \\ = &\frac {1} {n} \sum\limits_{i=1}^n(X_i-\mu)^2 - (\mu-\bar{X})^2 \end{aligned} n1i=1∑n(Xi−Xˉ)2====n1i=1∑n((Xi−μ)+(μ−Xˉ))2n1i=1∑n(Xi−μ)2+n2i=1∑n(Xi−μ)(μ−Xˉ)+n1i=1∑n(μ−Xˉ)2n1i=1∑n(Xi−μ)2+2(Xˉ−μ)(μ−Xˉ)+(μ−Xˉ)2n1i=1∑n(Xi−μ)2−(μ−Xˉ)2
换言之,除非正好 X ˉ = μ \bar{X} = \mu Xˉ=μ , 否则我们一定有
1 n ∑ i = 1 n ( X i − X ˉ ) 2 < 1 n ∑ i = 1 n ( X i − μ ) 2 \frac {1} {n} \sum\limits_{i=1}^n(X_i-\bar{X})^2 < \frac {1} {n} \sum\limits_{i=1}^n(X_i-\mu)^2 n1i=1∑n(Xi−Xˉ)2<n1i=1∑n(Xi−μ)2
所以把分母从n换成n-1,就是把对方差的估计稍微放大一点点。至于为什么是n-1,而不是n-2,n-3,…,有严格的数学证明。
无偏估计虽然在数学上更好,但是并不总是“最好”的估计,在实际中经常会使用具有其它重要性质的有偏估计。
12、协方差矩阵
协方差
通常,在提到协方差的时候,需要对其进一步区分。
(1)随机变量的协方差,跟数学期望、方差一样,是分布的一个总体参数。
(2)样本的协方差,是样本集的一个统计量,可作为联合分布总体参数的一个估计。在实际中计算的通常是样本的协方差。
样本的协方差
在实际中,通常我们手头会有一些样本,样本有多个属性,每个样本可以看成一个多维随机变量的样本点,我们需要分析两个维度之间的线性关系。协方差及相关系数是度量随机变量间线性关系的参数,由于不知道具体的分布,只能通过样本来进行估计。
设样本对应的多维随机变量为 X = [ X 1 , X 2 , X 3 , . . . , X n ] T X=[X_1,X_2,X_3,...,Xn]^T X=[X1,X2,X3,...,Xn]T,样本集合为{ x ⋅ j = [ x 1 j , x 2 j , . . . , x n j ] T ∣ 1 ⩽ j ⩽ m x⋅j=[x_{1j},x_{2j},...,x_{nj}]^T|1⩽j⩽m x⋅j=[x1j,x2j,...,xnj]T∣1⩽j⩽m}, m m m 为样本数量。与样本方差的计算相似, a a a和 b b b两个维度样本的协方差公式为,其中 1 ⩽ a ⩽ n 1⩽a⩽n 1⩽a⩽n, 1 ⩽ b ⩽ n 1⩽b⩽n 1⩽b⩽n, n n n为样本维度
q a b = ∑ j = 1 m ( x a j − x ˉ a ) ( x b j − x ˉ b ) m − 1 q_{ab}=\frac {\sum_{j=1}^m(x_{aj}-\bar{x}_a)(x_{bj}-\bar{x}_b)} {m−1} qab=m−1∑j=1m(xaj−xˉa)(xbj−xˉb)
这里分母为m−1是因为随机变量的数学期望未知,以样本均值代替,自由度减一。
标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系啊,协方差就是这样一种用来度量两个随机变量关系的统计量,我们可以仿照方差的定义:
v a r ( X ) = ∑ i = 1 n ( X i − X ˉ ) ( X i − X ˉ ) n − 1 var(X) = \frac {\sum_{i=1}^n(X_i-\bar{X})(X_i-\bar{X})} {n-1} var(X)=n−1∑i=1n(Xi−Xˉ)(Xi−Xˉ)
来度量各个维度偏离其均值的程度,协方差可以这么来定义:
c o v ( X , Y ) = ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) n − 1 cov(X, Y) = \frac {\sum_{i=1}^n(X_i-\bar{X})(Y_i-\bar{Y})} {n-1} cov(X,Y)=n−1∑i=1n(Xi−Xˉ)(Yi−Yˉ)
那么,协方差的结果有什么意义呢?如果结果为正值,则说明两个随机变量是正相关的(从协方差可以引出“相关系数”的定义),也就是说一个人越猥琐就越受女孩子欢迎,嘿嘿,那必须的~结果为负值就说明负相关的,越猥琐女孩子越讨厌,可能吗?如果为0,也是就是统计上说的“相互独立”。
从协方差的定义上我们也可以看出一些显而易见的性质,如:
1.
c
o
v
(
X
,
X
)
=
v
a
r
(
X
)
1. cov(X, X) = var(X)
1.cov(X,X)=var(X)
2.
c
o
v
(
X
,
Y
)
=
c
o
v
(
Y
,
X
)
2. cov(X, Y) = cov(Y, X)
2.cov(X,Y)=cov(Y,X)
协方差矩阵的由来
好几十年前,鲁迅爷爷就说过,世界上本没有路,走的人多了也就有了路。协方差矩阵也是这样,好多协方差凑合到一起就形成了协方差矩阵。当然,数学的定义,不能如我这样随意。对于一个二维矩阵,每一个因子都可以视为两个不同随机变量的关系,这正好和协方差矩阵多少有点牵连,因此数学家们就把协方差矩阵引入到了二维矩阵中,衡量各个变量之间的紧密程度(就是关系度啦)。根据协方差的性质,我们可以类似的推出协方差矩阵的性质:
1.协方差矩阵一定是个对称的方阵
2.协方差矩阵对角线上的因子其实就是变量的方差: c o v ( X , X ) = v a r ( X ) cov(X,X)=var(X) cov(X,X)=var(X)
这个定义还是很容易理解的,我们可以举一个简单的三变量的例子,假设数据集有{ x , y , z x,y,z x,y,z}{ x , y , z x,y,z x,y,z}三个维度,则协方差矩阵为:
( c o v ( x , x ) c o v ( x , y ) c o v ( x , z ) c o v ( y , x ) c o v ( y , y ) c o v ( y , z ) c o v ( z , x ) c o v ( z , y ) c o v ( z , z ) ) %开始数学环境 \left( %左括号 \begin{array}{ccc} %该矩阵一共3列,每一列都居中放置 cov(x, x)& cov(x, y) & cov(x, z)\\ cov(y, x)& cov(y, y) & cov(y, z)\\ cov(z, x)& cov(z, y) & cov(z, z) \end{array} \right) %右括号 ⎝⎛cov(x,x)cov(y,x)cov(z,x)cov(x,y)cov(y,y)cov(z,y)cov(x,z)cov(y,z)cov(z,z)⎠⎞
再一次可以看出,协方差矩阵是一个对称的矩阵,而且对角线是各个变量上的方差。
心得感悟
理解协方差矩阵的关键就在于牢记它计算的是不同维度之间的协方差,而不是不同样本之间,拿到一个样本矩阵,我们最先要明确的就是一行是一个样本还是一个维度,心中明确这个整个计算过程就会顺流而下,这么一来就不会迷茫了。
其实还有一个更简单的容易记还不容易出错的方法:协方差矩阵一定是一个对称的方阵,一定是一个对称的方阵,一定是一个对称的方阵!!!记住就好啦~
13、流形学习概述
14、关于感受野的总结
15、深度学习中Embedding层有什么用?
16、GAN
GAN的思想就是一个博弈的思想。GAN有两个互相对抗的模型,一个生成模型G用于拟合样本数据分布和一个判别模型D用于估计输入样本是来自于真实的训练数据还是生成模型G。我们让两个网络相互竞争,生成网络来生成假的数据,对抗网络通过判别器去判别真伪,最后希望生成器生成的数据能够以假乱真。
判别网络的目的:就是能判别出来属于的一张图它是来自真实样本集还是假样本集。假如输入的是真样本,网络输出就接近1,输入的是假样本,网络输出接近0,那么很完美,达到了很好判别的目的。
生成网络的目的:生成网络是造样本的,它的目的就是使得自己造样本的能力尽可能强,强到什么程度呢,你判别网络没法判断我是真样本还是假样本。(不需要像传统图模型一样,需要一个严格的生成数据的表达式。这就避免了当数据非常复杂的时候,复杂度过度增长导致的不可计算。同时,它也不需要 inference 模型中的一些庞大计算量的求和计算。它唯一的需要的就是,一个噪音输入,一堆无标准的真实数据,两个可以逼近函数的网络。)
在训练网络时:
(1)训练判别器。
• 固定生成器
• 对于真图片,判别器的输出概率值尽可能接近 1
• 对于生成器生成的假图片,判别器尽可能输出 0
(2)训练生成器。
• 固定判别器
• 生成器生成图片,尽可能让判别器输出 1
(3)返回第一步,循环交替训练。
训练生成器时无须调整判别器的参数;训练判别器时,无须调整生成器的参数。
其中的损失函数应用了最大最小优化问题:
min
G
max
D
V
(
D
,
G
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\min\limits_G\max\limits_D V(D, G) = E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]
GminDmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
(z表示输入G的随机噪声)
训练模型D要最大概率地分对真实样本(最大化 log ( D ( x ) ) \log(D(x)) log(D(x)),而生成模型G要最小化 log ( 1 − D ( G ( z ) ) ) \log(1-D(G(z))) log(1−D(G(z))) ,即最大化D的损失。G和D同时训练,但是训练中要固定一方,更新另一方的参数,交替迭代,使对方的错误最大化。最终,G能估计出真实样本的分布。
上面那个loss函数可以分开看成下面的两个公式。
优化D:
max
D
V
(
D
,
G
)
=
E
x
∼
p
d
a
t
a
(
x
)
[
log
D
(
x
)
]
+
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\max\limits_D V(D, G) = E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]
DmaxV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
优化G:
min
G
V
(
D
,
G
)
=
E
z
∼
p
z
(
z
)
[
log
(
1
−
D
(
G
(
z
)
)
)
]
\min\limits_G V(D, G) = E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]
GminV(D,G)=Ez∼pz(z)[log(1−D(G(z)))]
可以看到,优化D的时候,也就是判别网络,其实没有生成网络什么事,后面的G(z)这里就相当于已经得到的假样本。优化D的公式的第一项,使的真样本x输入的时候,得到的结果越大越好,可以理解,因为需要真样本的预测结果越接近于1越好嘛。对于假样本,需要优化是的其结果越小越好,也就是D(G(z))越小越好,因为它的标签为0。但是呢第一项是越大,第二项是越小,这不矛盾了,所以呢把第二项改成1-D(G(z)),这样就是越大越好,两者合起来就是越大越好。 那么同样在优化G的时候,这个时候没有真样本什么事,所以把第一项直接却掉了。这个时候只有假样本,但是我们说这个时候是希望假样本的标签是1的,所以是D(G(z))越大越好,但是呢为了统一成1-D(G(z))的形式,那么只能是最小化1-D(G(z)),本质上没有区别,只是为了形式的统一。之后这两个优化模型可以合并起来写,就变成了最开始的那个最大最小目标函数了。
也就是说,在训练过程中,会把生成模型生成的样本和真实样本随机地传送一张(或者一个 batch)给判别模型 D。判别模型 D 的目标是尽可能正确地识别出真实样本(输出为“真”,或者1),和尽可能正确地揪出生成的样本,也就是假样本(输出为“假”,或者0)。而生成模型的目标则和判别模型相反,就是尽可能最小化判别模型揪出它的概率。这样 G 和 D 就组成了一个min-max,在训练过程中双方都不断优化自己,直到达到平衡——双方都无法变得更好,也就是假样本与真样本完全不可区分。
- 李宏毅2017深度学习 GAN生成对抗神经网络相关学习视频合集
体会:如果GAN能够学出真实样本的分布,那么把G和D拆开看,它们各自的功能是什么?
而在分割网络结果上,进行判别性学习,是否能够使目标域学习到源域的分布?
17、图神经网络和传统图模型,以及深度学习间的关系
机器之心: 您可以介绍一下图神经网络和传统图模型,以及原来的深度学习之间的关系吗?
刘知远: 对于这个问题,我们需要看是从什么角度来考虑。
从研究任务的角度来看,比如数据挖掘领域的社会网络分析问题
- 像 DeepWalk、LINE 这些 graph embedding 算法,聚焦在如何对网络节点进行低维向量表示,相似的节点在空间中更加接近。
- 图神经网络(GNN)
① GNN可以对一个节点进行语义表示。
GNN可以更好地考虑这个节点周围的丰富信息,对单个节点的表示也可以做的比过去方法更好。
② GNN可以表示子图的语义信息。
GNN可以把网络中一小部分节点构成的社区(community)的语义表示出来,这是 graph embedding 不容易做到的。
③ GNN可以把网络当成一个整体进行建模。
它可以在整个网络上进行信息传播、聚合等建模。
知识图谱
- TransE 等知识表示学习方法,一般是将知识图谱按照三元组来学习建模,学到每个实体和关系的低维向量表示,这样就可以去进行一些链接预测和实体预测任务。
- GNN 则有希望把整个知识图谱看成整体进行学习,并可以在知识图谱上开展注意力、卷积等操作,以学习图谱中实体与实体之间的复杂关系。即使实体间没有直接连接,GNN 也可以更好地对它们的关系建模。
关系
- 随机游走、最短路径等图方法利用知识图谱这种符号知识,但这些方法并没有办法很好地利用每个节点的语义信息。
- 传统的深度学习技术更擅长处理非结构文本、图像等数据。
- 简言之,我们可以将 GNN 看做将深度学习技术应用到了符号表示的图数据上来,或者说是从非结构化数据扩展到了结构化数据。GNN 能够充分融合符号表示和低维向量表示,发挥两者优势。
总结:传统图模型应该是要学习实体以及关系,不限于单个,但是没学好;传统的深度学习,只能学习单个实体的语义信息;图神经网络使得深度学习学习实体与实体之间的关系成为可能。
- 原文:对话清华NLP实验室刘知远:NLP搞事情少不了知识库与图神经网络
- 清华大学图神经网络综述:模型与应用
Graph Neural Networks: A Review of Methods and Applications- DeepMind 等机构提出「图网络」:面向关系推理
Relational inductive biases, deep learning, and graph networks
17、什么是零样本学习?

在过去的几十年里机器变得更聪明了,但是没有一定量的标注训练数据,机器是无法区分两个很相似的物体的。另一方面,人类能够识别将近3万个基本物体类别。在机器学习中,这被称为零样本学习(ZSL)。考虑一个例子,一个小孩可以很容易识别一个斑马,如果他之前就看过马并且了解到斑马和马很像,但是有黑白的条纹。
对机器来说,零样本识别依赖于可见类的一个标注数据集和关于每个不可见类如何与可见类语义相关的知识的存在。根据一篇研究论文,人类能够实现零样本学习是因为已有的语言知识基础,这为一个新的或不可见的类别提供了高层描述,并且建立了不可见类、可见类和视觉概念(马,条纹)的关联。受人类这项能力的激发,人们对机器零样本学习越来越感兴趣,以扩大视觉识别领域。
零样本学习 101
有研究称,零样本机器学习是用来构建没有标注训练数据的不可见目标类的识别模型。ZSL利用类别属性作为辅助信息,迁移从带有标注样本的源类的信息。ZSL包含两个阶段:
①训练:这个阶段获取属性的知识
②推理:用获取的知识识别新类别的实例
最近,由于包含元数据信息的数据的可用性,人们对属性的自动识别兴趣大增。一篇研究论文称,已被证明这对识别图像是特别有用的。
一项研究称,零样本学习方法设计的目的是学习中间语义层,他们的属性,并在推理阶段应用他们来预测数据的类别。
另一项研究进一步解释,零样本学习也依赖于可见类和不可见类的一个标注数据集。可见类和不可见类在一个高维向量空间是相关的,这个空间叫做语义空间,在这个空间里可见类的知识可以迁移到不可见类。
利用语义空间和图像内容的视觉特征表示,一组研究人员用两步来解决ZSL问题:
- 学习一个联合的嵌入空间,其中语义向量(原型)和视觉特征向量都被投影到这个空间。
- 使用最近邻搜索在嵌入空间匹配图像特征的投影和未见类的原型的投影。
实现零样本学习
为了使ZSL更高效,将关键特征(图像和文本)分类[提取]成向量。这意味着要预先为项目寻找特定的向量。一旦收集完毕,就给他们提供一个描述,使得算法能够进行相应地分类。训练是对这些向量进行对应类别的分类。测试阶段识别新输入,并再次识别成新的类别,忽略训练数据。
实现中步骤
一个教程描述了一个模型实现ZSL的三个步骤:
- 得到类别向量V:
- 属性:描述了概念或者实例的视觉外观,通过设定标注的视觉特性,他们可以很容易从可见类迁移到不可见类。
- 词向量:它是对其他数据类型的直接应用,比如视频、文本和音频,
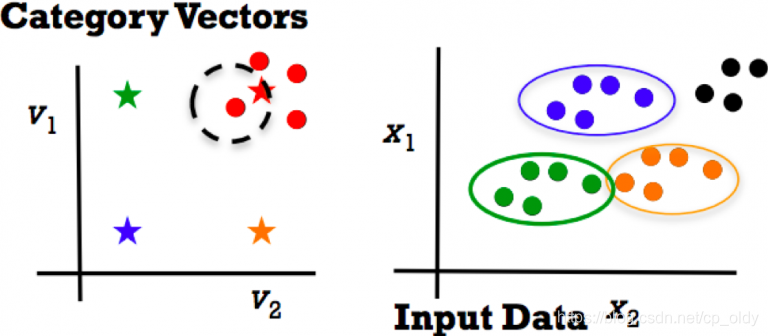
- 训练:
- 给定一些已知类的类别向量V和图像X
- 学习图像,通过将他们分类为向量分类器或者回归器 V=F(X) - 测试:
- 为要识别的新类指定向量V
- 映射测试数据F(X)到类别向量空间
- V 和 F(X)的最近邻匹配
深度零样本学习
从前,ZSL工作使用物体的手工特征表示。在过去两年手工特征已经被CNN特征取代来作为视觉特征表示。这里,使用预训练的CNN模型来提取特征。深度CNN特征也是嵌入模型的输入。现有的基于深度网络的ZSL工作的不同之处在于他们是否使用了语义空间或者一个中间表示作为嵌入空间。
怎么训练一个深度的端到端的ZSL
- 训练E(X, Z),对于匹配的数据对是大的,对于不匹配的对是小的
- 让E(X, Z)是一个网络而不是一个双线性模型
- 连接(X, Z)并输入到一个深度网络里
- 在X和Z上做表示学习,然后是內积
在Timothy的教程中解释的一个简单的ZSL深度网络
Train a max-margin ranker. Or Y=(1,0) for (matching, mismatching pair) pairs.
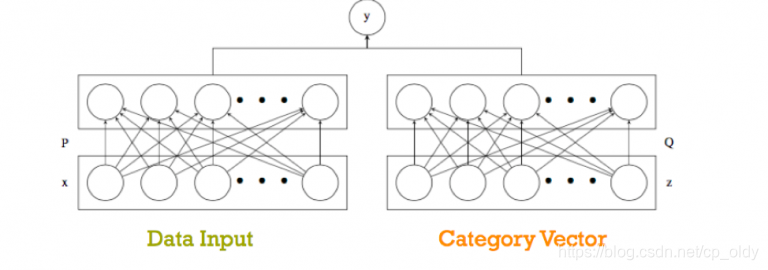
根据一项研究,尽管深度神经网络在其他视觉问题上比如图像描述的成功,它学习了文本和图像间的端到端的模型,但是深度的ZSL模型还很少。深度ZSL模型相对于只利用深度特征表示而不进行端到端嵌入学习的ZSL模型并没有显示出很多的优势。























 458
458

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








