LeetCode Hot100 No.94 二叉树中序遍历

给定一个二叉树的根节点 root ，返回它的 中序 遍历。
示例 1：

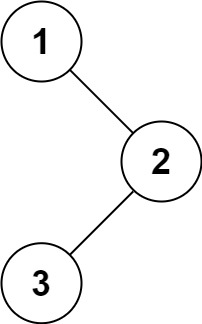
输入：root = [1,null,2,3]
输出：[1,3,2]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]

示例 4：

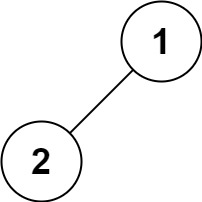
输入：root = [1,2]
输出：[2,1]

示例 5：

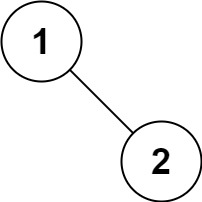
输入：root = [1,null,2]
输出：[1,2]

我的思路：
先来分析中序遍历什么时候该弹栈，什么时候该压栈。
压栈：
1.当前栈顶节点左子树不为null,且未遍历过左子树。
2.当前栈顶节点左子树为null,或已经遍历完。右子树不为null，则需要先将栈顶弹出，再将右子树入栈。

弹栈：
1.如果栈顶节点的左子树为null或已经遍历完，则栈顶节点出栈。中序遍历的情况下，根节点的左节点紧跟在根节点之后被压栈，该根节点的左节点被弹出后，紧跟其后就要弹出根节点。

用一个标记变量来记录当前栈顶节点是否需要弹出，为1则说明当前栈顶需要弹出。具体操作是，如果此次循环标记变量为1或者当前栈顶左节点为空，则先将栈顶出栈，再判断其右子树是否为空，不为空则将右节点压栈，标记变量置为0。若右子树为空，标记变量还为1不变。
其实可以用一个指针记录前一个被弹出的节点，然后将当前栈顶的左节点和该指针比较，若相同或左节点为null就弹出当前栈顶节点。并将指针重定向到弹出的节点。判断右节点是否为空，不为空则入栈。为空则不作操作，进入下一循环。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
          List<Integer> l = new ArrayList<>();
        Deque<TreeNode> stack =new LinkedList<>();
        int lfTrDone = 0;
        if(root==null)
            return l;
        stack.push(root);
        while(!stack.isEmpty())
        {
            TreeNode top = stack.peek();
            if(top.left==null||lfTrDone==1)//表示当前栈顶节点的左子树已经遍历完或为空
            {
                stack.pop();//栈顶出栈
                l.add(top.val);
                if(top.right==null)
                    lfTrDone=1;//告诉当前栈顶节点，你的左子树遍历完了！
                else 
                {
                    stack.push(top.right);
                    lfTrDone = 0;//当前栈顶节点刚入栈，其左子树一定还未遍历，所以置为0
                }
                
            }
            else{
                stack.push(top.left);//当前栈顶节点的左子树没遍历且不为空，左子树根节点入栈
            }
        }
        return l;
    }
}

另一种做法

class Solution {
	public List<Integer> inorderTraversal(TreeNode root) {
		List<Integer> res = new ArrayList<Integer>();
		Stack<TreeNode> stack = new Stack<TreeNode>();
		while(stack.size()>0 || root!=null) {
			//不断往左子树方向走，每走一次就将当前节点保存到栈中
			//这是模拟递归的调用
			if(root!=null) {
				stack.add(root);
				root = root.left;
			//当前节点为空，说明左边走到头了，从栈中弹出节点并保存
			//然后转向右边节点，继续上面整个过程
			} else {
				TreeNode tmp = stack.pop();
				res.add(tmp.val);
				root = tmp.right;
			}
		}
		return res;
	}
}