直接插入排序与希尔排序

一、直接插入排序

1.基本概念

2.代码实现

3.时间复杂度

二、希尔排序

1.基本概念

2.代码实现

3.时间复杂度

一、直接插入排序

1.基本概念

把待排序的记录按其关键码值的大小逐个到一个已经排好序的有序序列中，直到所有的记录都插入完为止，得到一个新的有序序列。

由下图可知，当插入第i个元素时，前面的已经排好序了，此时arr[i]的排序码与arr[i-1]，arr[i-2]......的排序码依次比较，找到插入的位置，将arr[i]插入，原来的的位置元素顺序后移。

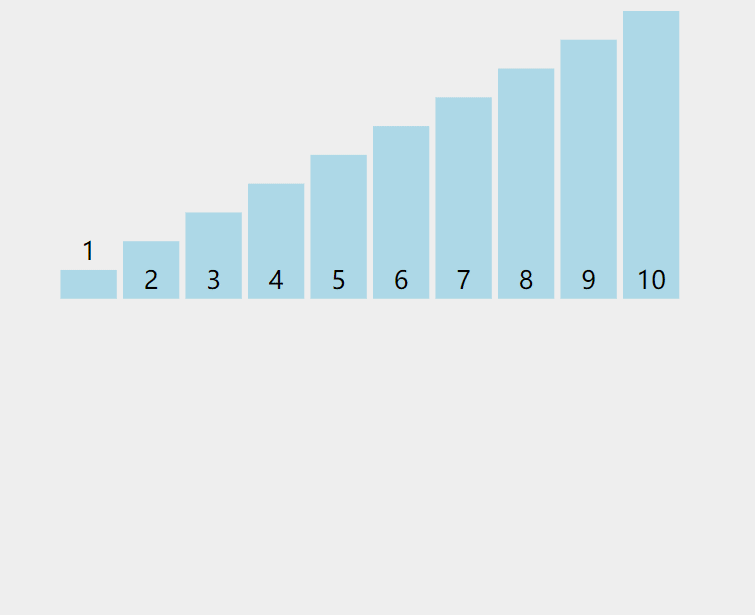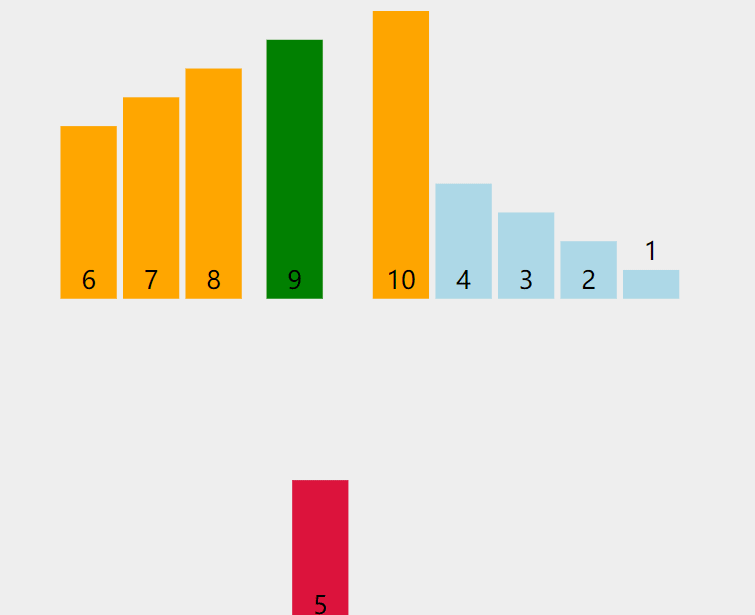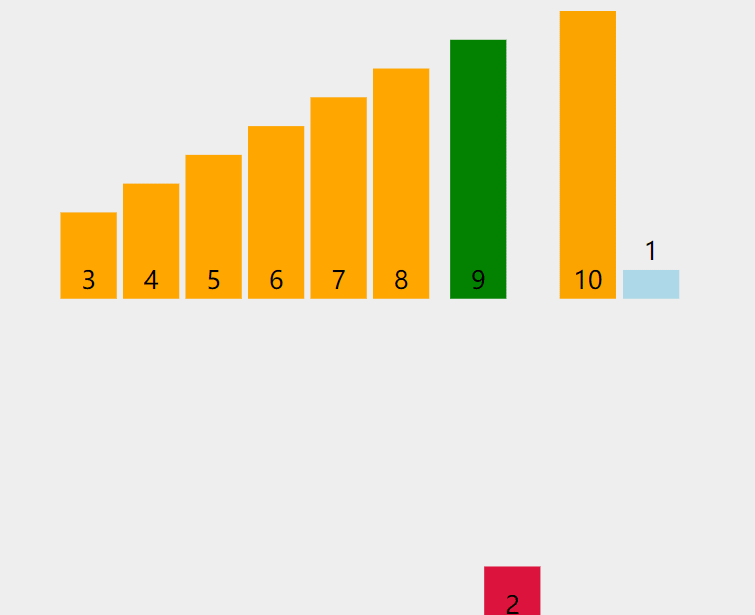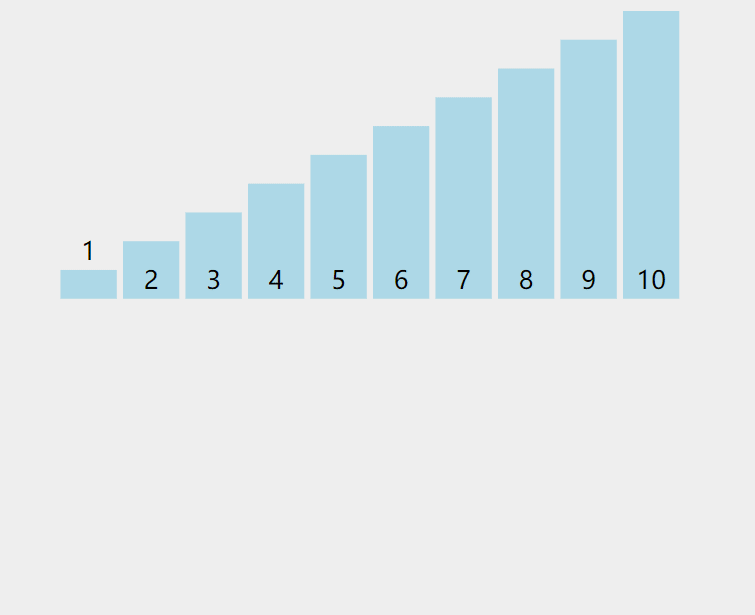
2.代码实现

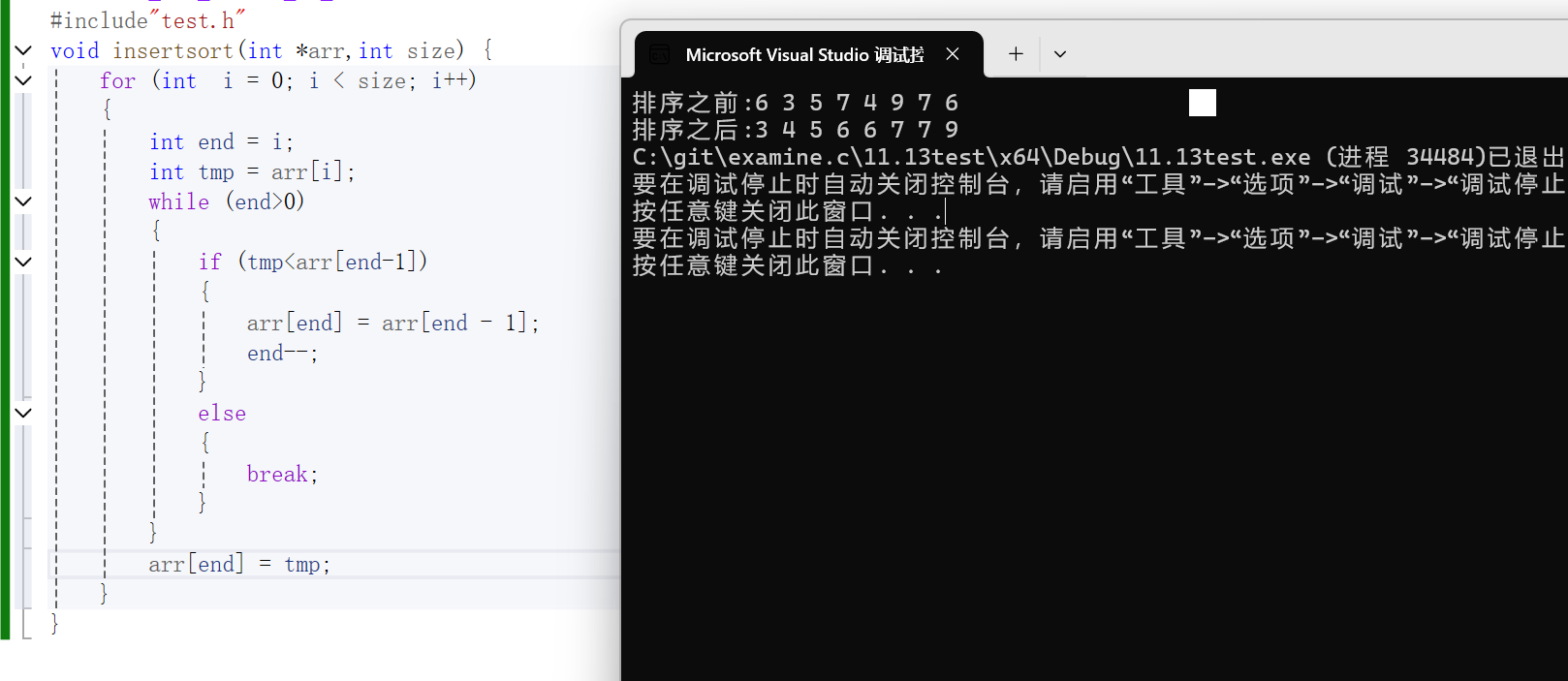
3.时间复杂度与空间复杂度

时间复杂度分析：一个for循环中，嵌套着一个while循环，当时间复杂度为最坏时，那么时间复杂度为T(N^2)；当时间复杂度为最好时，意味着while一直break跳出，所以时间复杂度为O(N)。

空间复杂度：O（1）

二、希尔排序

1.基本概念

希尔排序又叫缩小增量法。希尔排序的基本思想是：先选定一个整数为gap=n/3+1,把待排序的排序文件所有记录分成各组，所有的距离相等的记录分在同一组内，并对每一组的记录进行排序，然后gap=gap/3+1得到下一个整数，再将数组分成各组，进入插入排序，当gap=1，就相当于直接插入排序。

下图是希尔排序的大致方法，如果gap=5时，下标为0和小标为5的位置进行比较，而后是小标为1与小标为6，由此可知gap是步长。当到了下标为5时最后一个数也比较完了，所以gap第一趟排序完毕。接着继续将gap/3+1此时gap=2，按照前面gap为步长，以步长分组。接着到下标奇数的为一组，为偶数的为一组进行排序。当gap=1时，此时变成了直接插入排序。

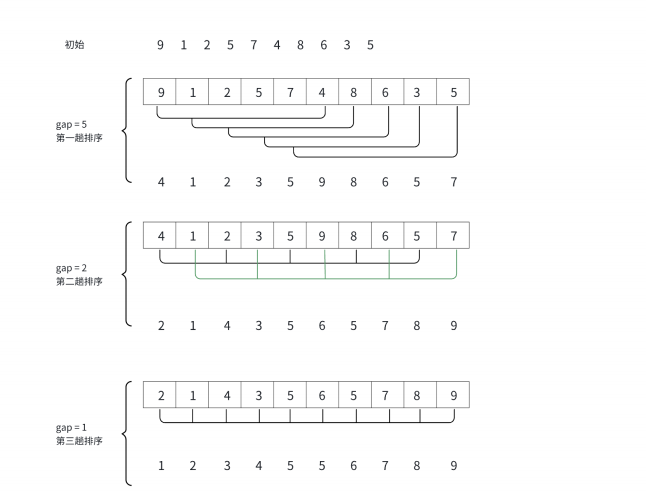
2.代码实现

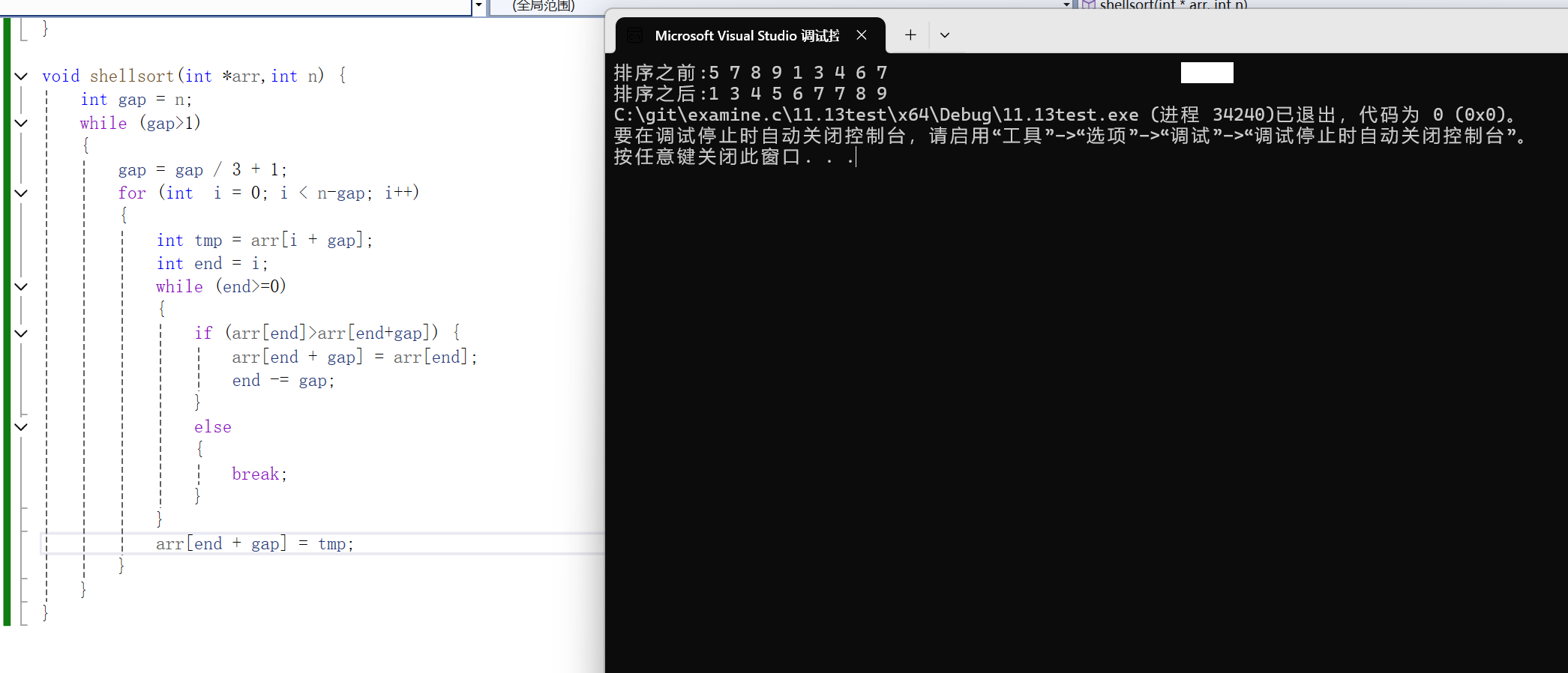
3.时间复杂度

时间复杂度分析：外层循环为O（logn），

假设⼀共有n个数据，合计gap组，则每组为n/gap个；在每组中，插⼊移动的次数最坏的情况下为

，⼀共是gap组，因此：

1 + 2 + 3 + .... + ( gap/n − 1))

总计最坏情况下移动总数为： gap ∗ [1 + 2 + 3 + .... + ( gap/ n -1)]

gap取值有（以除3为例）：n/3 n/9 n/27 ...... 2  1

当gap为n/3时，移动总数为： 3 / n (1 + 2) = n

当gap为n/9时，移动总数为： 9 /n* (1 + 2 + 3 + .... + 8) =  9/ n* =（2 /8(1 + 8) ）=4n

最后⼀躺，gap=1即直接插⼊排序，内层循环排序消耗为n

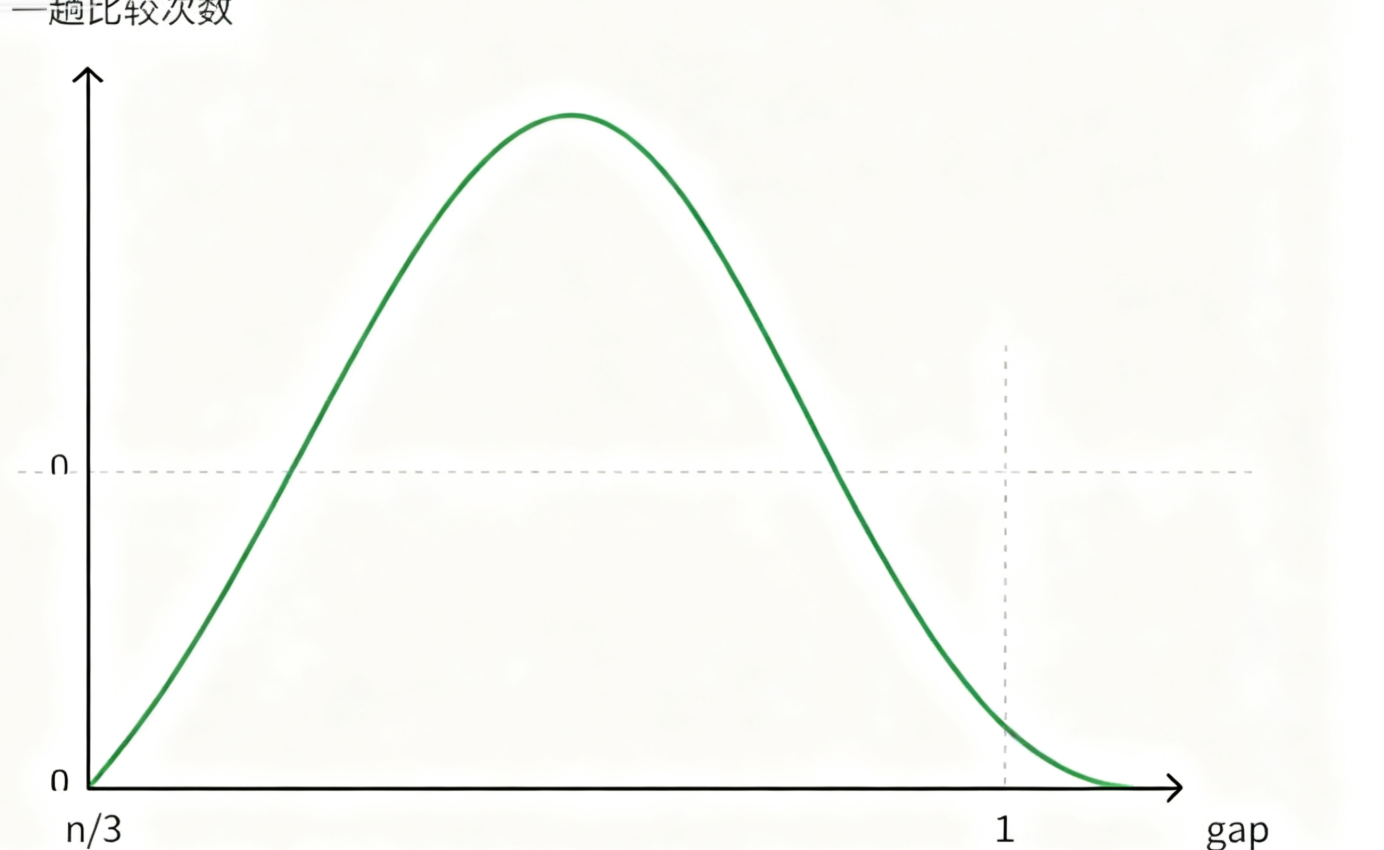
通过以上分析可以得到下面的曲线图。

希尔排序的时间复杂度为O（n^1.3）.