链式二叉树的实现

一、链式二叉树的概念

二、二叉树的操作实现

        前序遍历

        中序遍历

        后序遍历

        计算树结点的个数

        计算叶子结点个数

        计算k层结点个数

        查找值是否存在

        层序遍历

        判断是否为完全二叉树

三、代码的呈现

函数定义

函数调用

函数功能

一、链式二叉树的定义

用链表表示一颗二叉树，用链来指示元素的逻辑关系。通常的方法由链表中每个结点由三个域组成，数据域与左右指针域，左右指针分别用来给出左孩子和右孩子的存储地址。

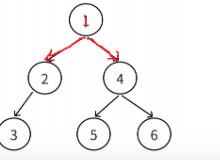
二、二叉树的操作实现

1.前序遍历

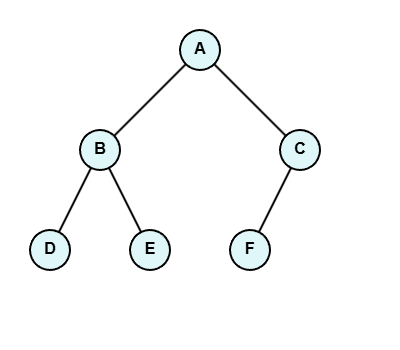
根据根左右的顺序进行打印，通过递归的方式。先将结点的值进行打印A，而后进行向左走，向左走后继续打印B，打印B之后继续递归左节点进行打印D，然后从在找D的左节点，因为D的做结点为NULL，直接返回D结点，而后找D的右结点，D的右节点也为NULL，这时打印了D的左右结点和D，即返回到B结点，因为B结点的左边已经处理完了，然后找B的右结点。找到E后将其打印，在找E的左结点为空即返回E结点，再去找E的右结点为NULL将其打印输出，这是B的左右结点都处理完了，返回B，B也处理完了返回A。前面是关于A的左边的推导。因为A左边已经算完了，这时我们需要计算右边的树。从A往右走到达C即打印，在从C的左节点开始打印F，此时到了F，在判断其左右结点，都为NULL直接返回，这是F的结点处理完了，需要返回C这个结点，因为C的右结点还没有处理，继续取C的右节点去找，因为C的右节点为NULL，直接输出NULL。这时A的右子树处理完毕，此时返回即遍历结束。

遍历顺序为

A    B   D    NULL    NULL   E   NULL   NULL   C   F   NULL   NULL   NULL

2.中序遍历

打印顺序为左根右。将根节点一直往左走直到D的左结点为止，因为D的左节点不存在，所以打印NULL，这时左节点处理完，返回D结点，将其打印为D，此时在处理D的右节点，因为它不存在。所以打印NULL，这时因为D结点都处理完毕，此时返回到D的父节点，直接将其打印为B，因为B的左边都处理完毕，此时要处理B的右边，到了E后，需要先找其左结点，此时结点为NULL，所以打印NULL；返回E并打印E，在打印E的右节点，右节点为NULL，打印NULL。关于A的左边都输出完毕。在打印根结点A。这时需要处理A的右边找到C，用C去找其中的左子树，因为左子树的到F的左节点为NULL，所以打印NULL。而后返回F，因为F的左边已经没有东西可以打印了，即打印F，在处理F的右边为NULL，打印NULL。这时C的左边都处理完毕，即打印C，然后处理C的右边。C的右边为NULL，所以直接打印NULL。这时遍历完毕。

遍历顺序为 

NULL   D   NULL   B   NULL   E   NULL   A   NULL   F   NULL   C   NULL

3.后序遍历

打印顺序为左右根。先让根节点一直往左走，直到D的左节点开始返回。因为D的左和右结点都为NULL，所以打印两个NULL。这时返回D结点直接将D打印，这时返回到B，然后执行B的的右边找到了E的左右结点，打印两个NULL。此时因为E的左右结点都打印过了，返回到E后直接打印E。这时处理完了B的左右子树，在打印B结点。这时 A左边的子树，都处理完了，这时需要处理A的右边。到了C后我们需要去往C的左边一直走，此时F的左右结点为NULL，打印两个NULL。在打印F，此时处理完了C的左边，这时需要处理右边这时C的右子树为NULL，打印NULL。这时子树的左右都处理完了，接下来打印根结点的值

遍历顺序为

 NULL    NULL      D     NULL    NULL   E   B   NULL   NULL   F   NULL   C   A

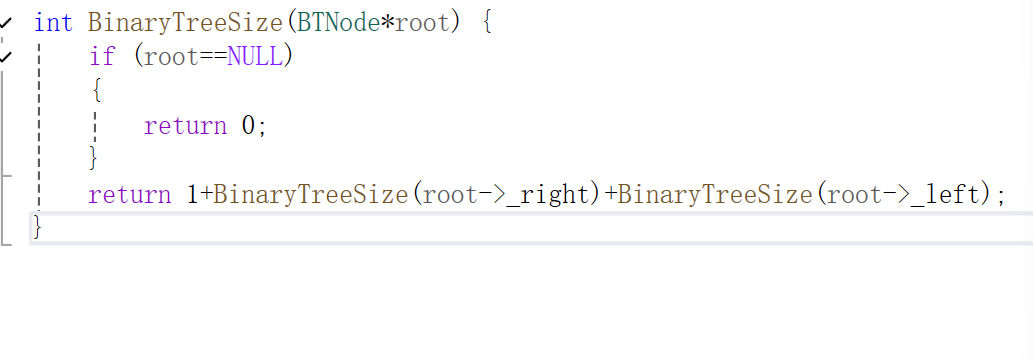
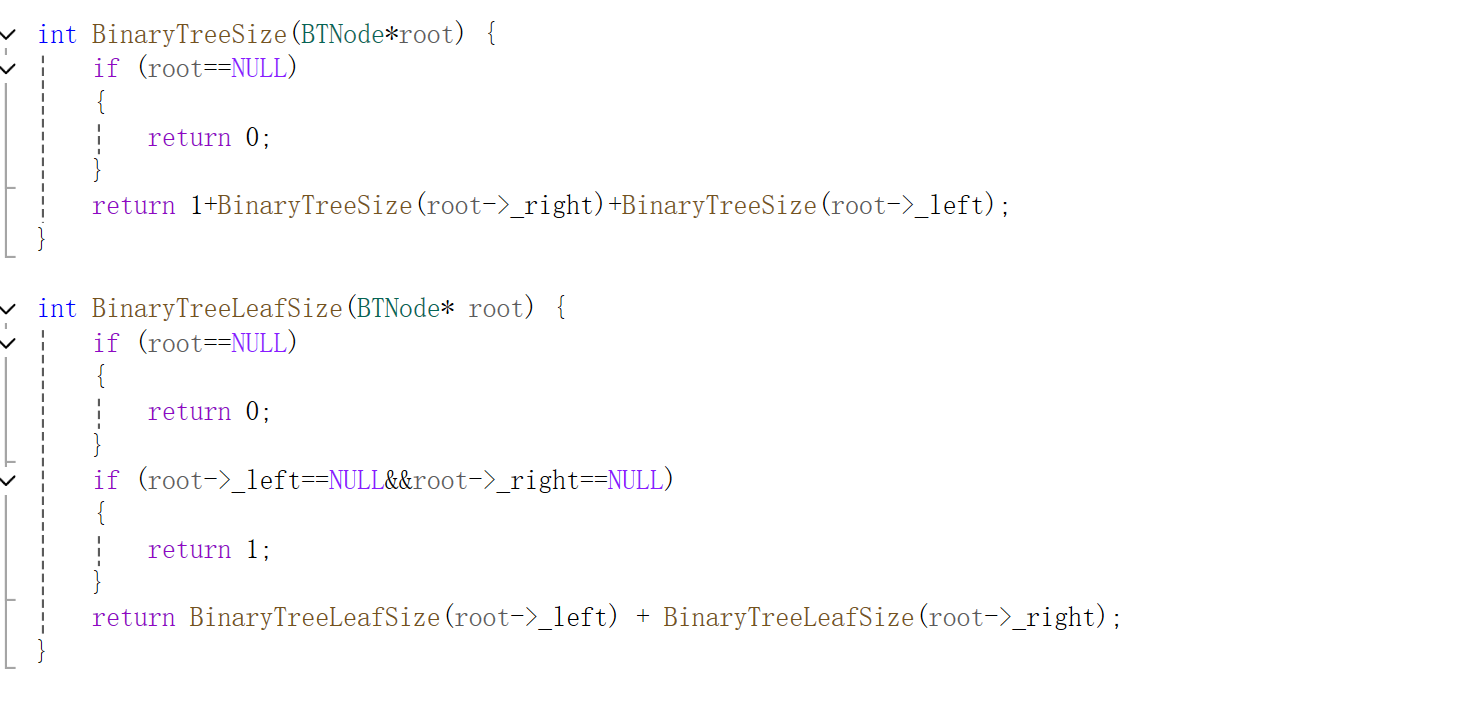
4.计算结点的个数

通过递归的方式，加个判断遇到空值时返回0；结点个数等于1（根节点）+左节点的个数+右节点的个数。

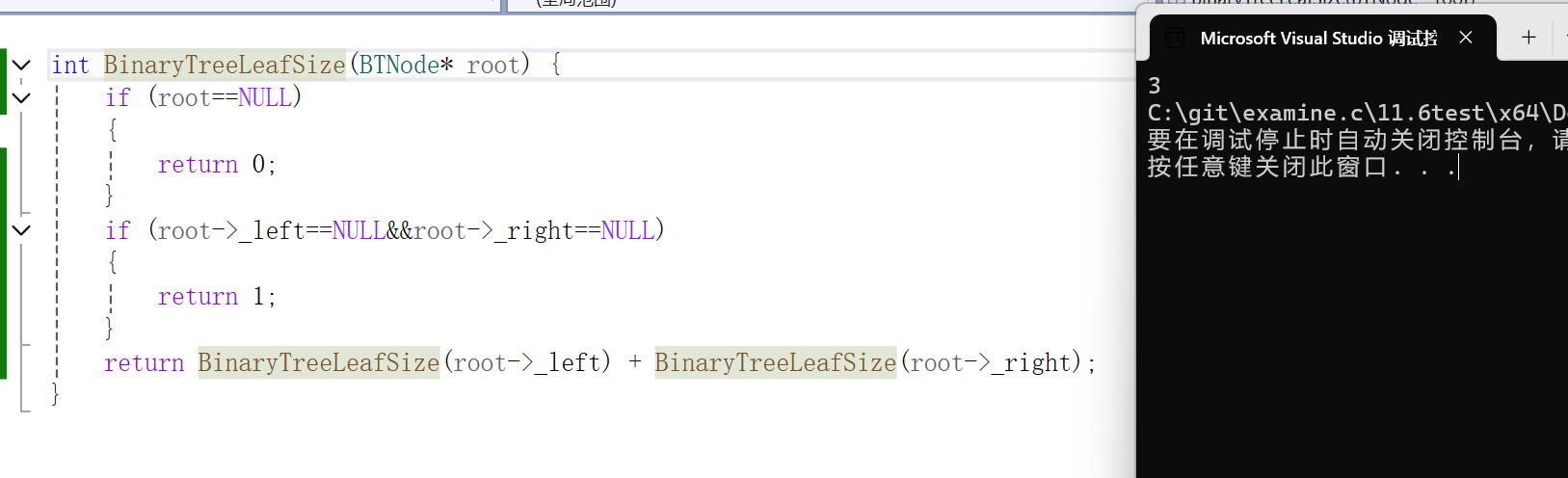
5.计算叶子节点个数

先判断其本身为NULL,为NULL则返回0。只需要直到叶子节点的概念，满足叶子的条件时他的左右结点都为NULL，故当满足该条件时输出1。最后通过递归左右子树，最后返回左子树的叶子结点+右子树的叶子节点。

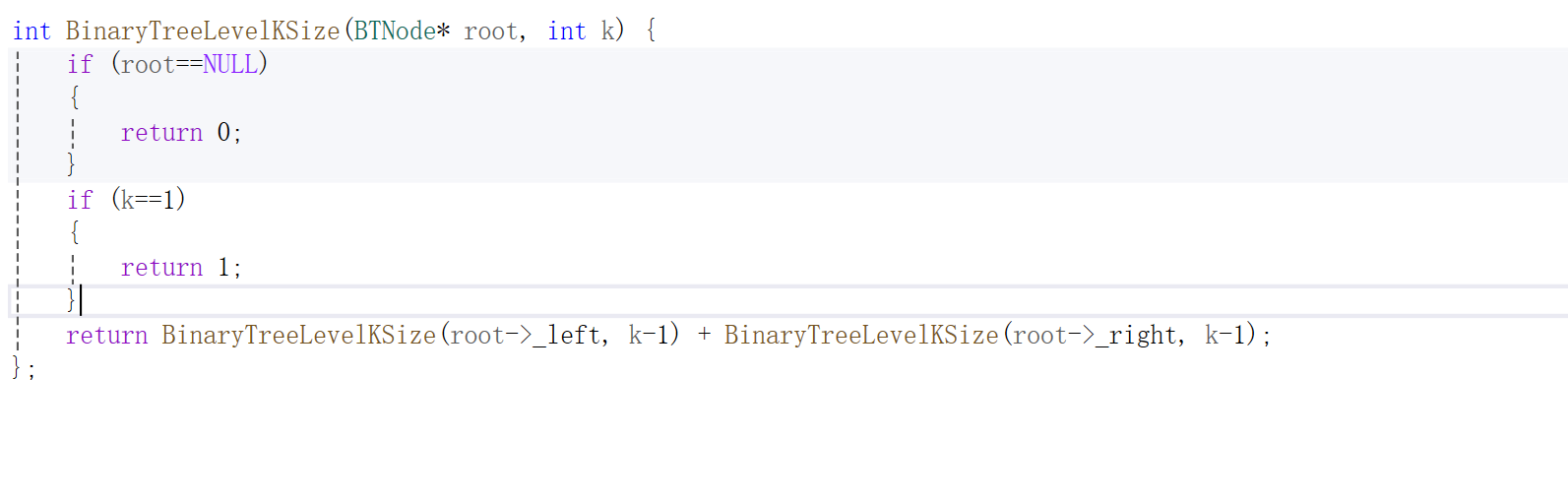
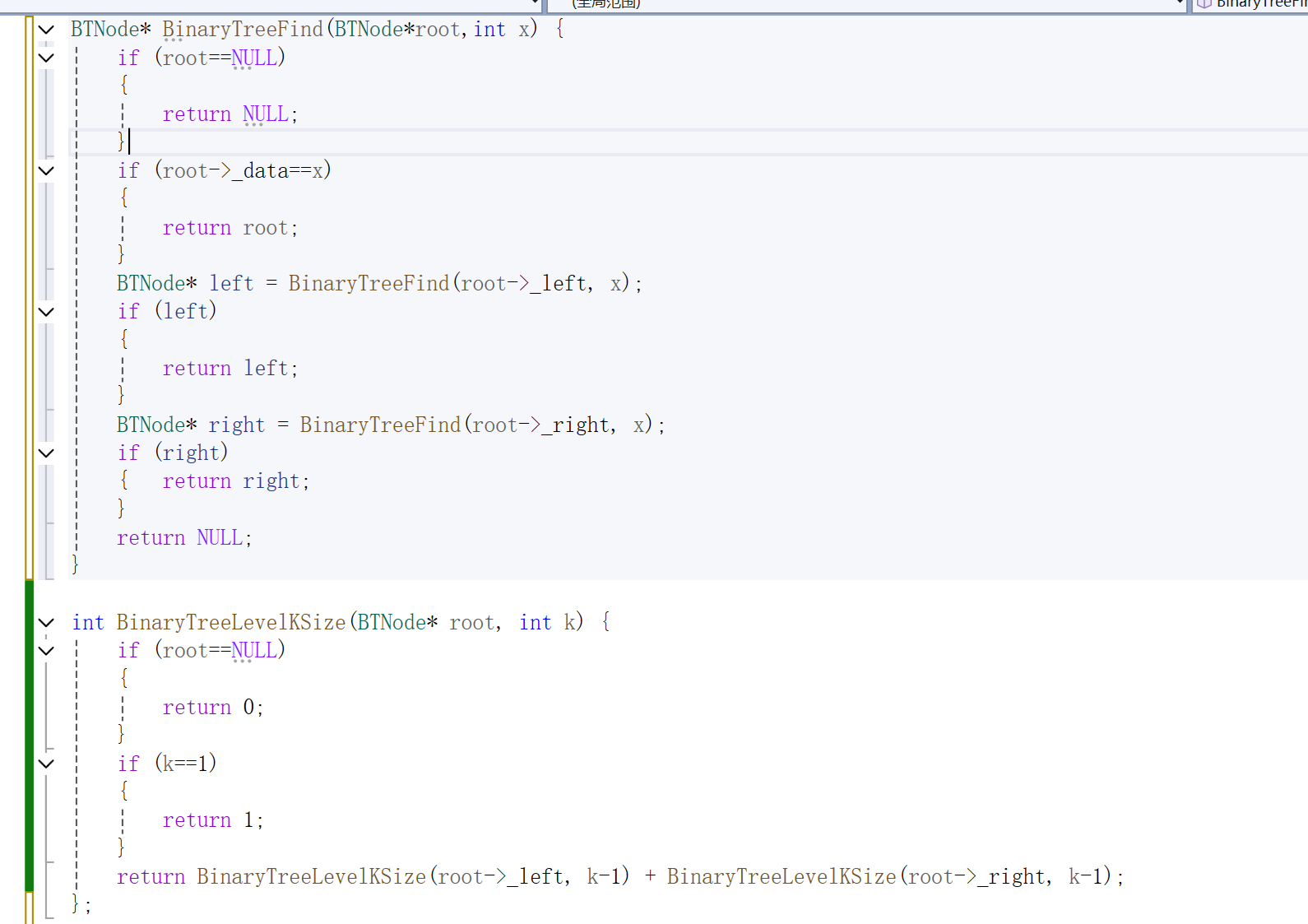
6.计算第k层结点个数

计算k层需要k等于即可到其需要计算的层数，直接判断该层的结点个数。利用递归。

7.查找x值是否存在

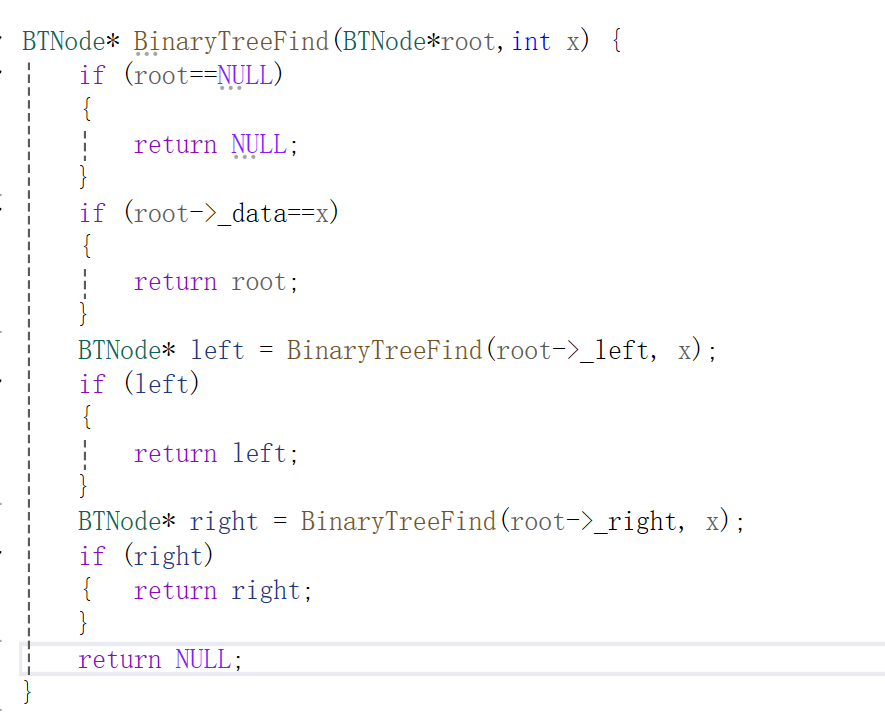
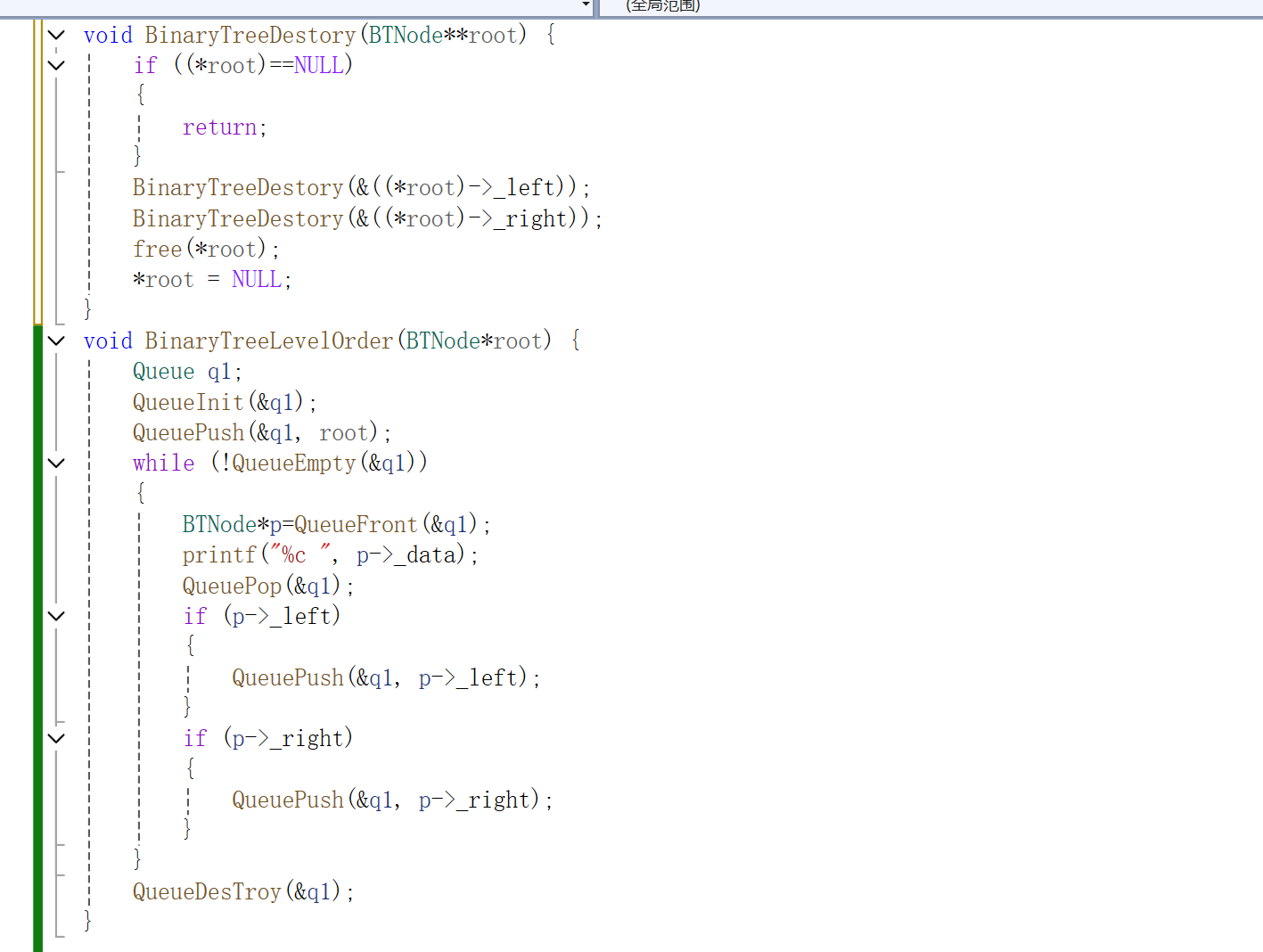
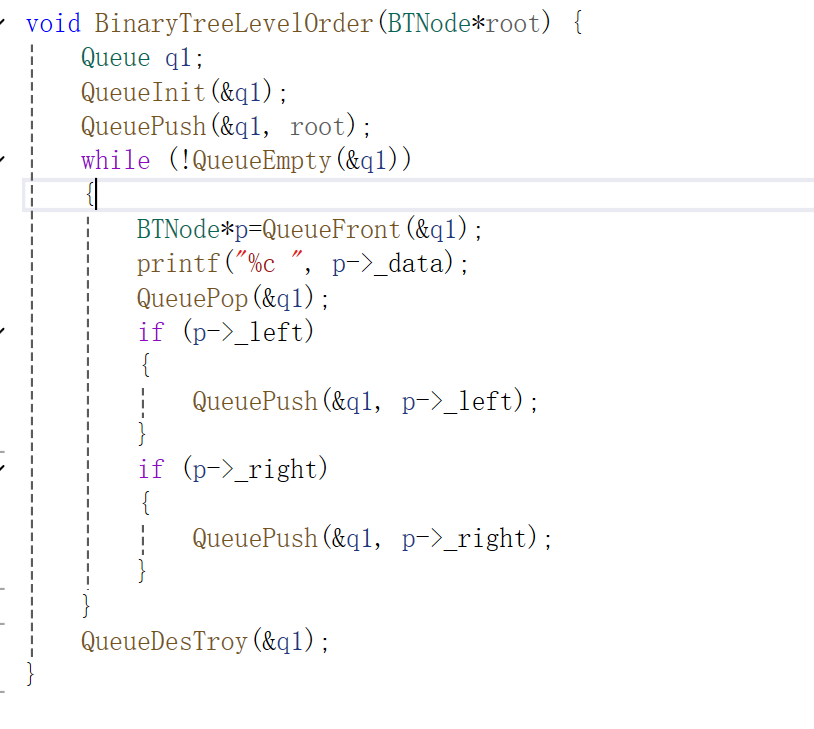
8.层序遍历

需要利用队列这个数据结构，先将root结点入队，进循环遍历，先将这根结点打印，并且出队，利用一个变量来存值，判断其左右是否存在，存在即入队。当队列没数时直接返回。

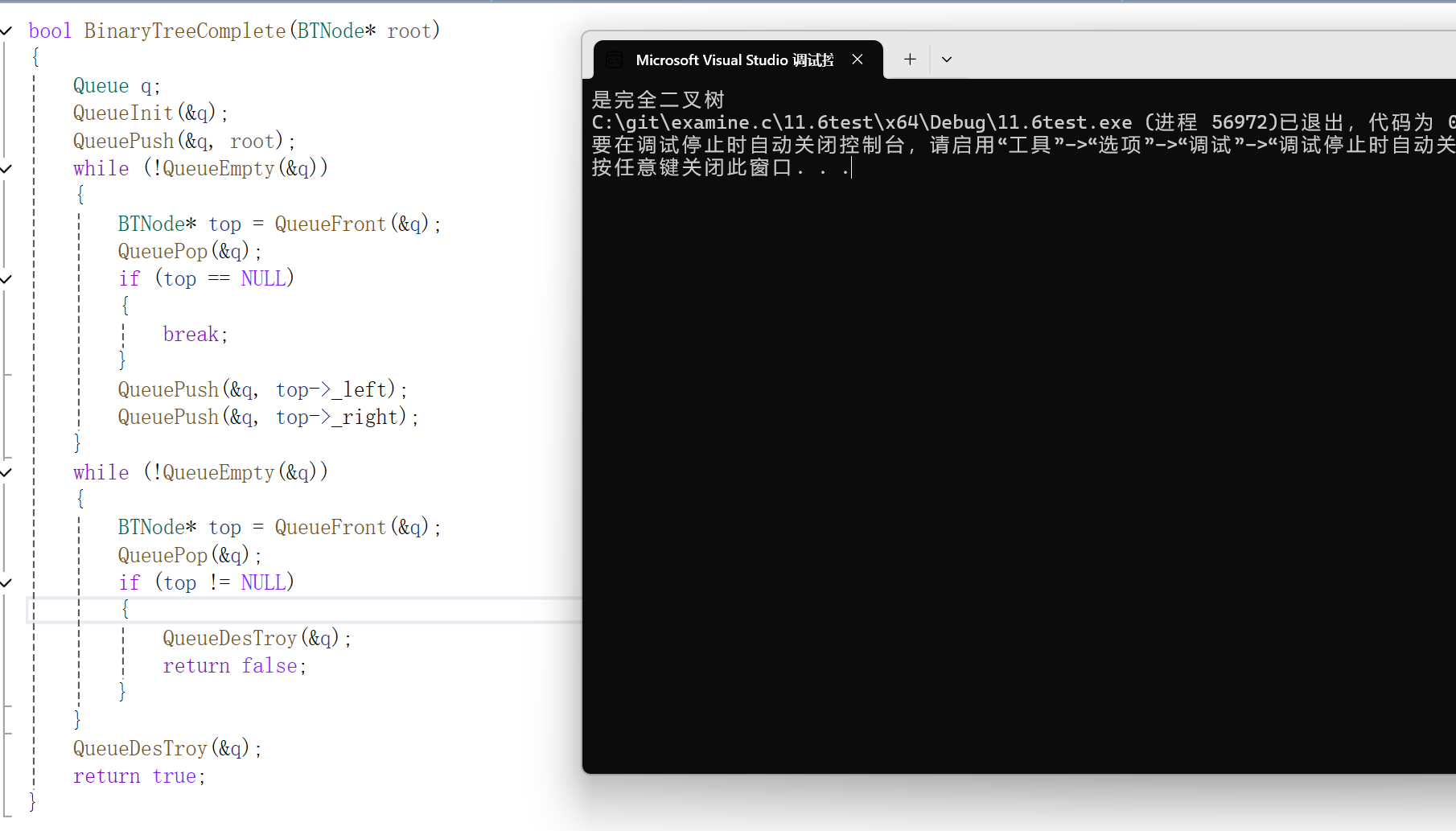
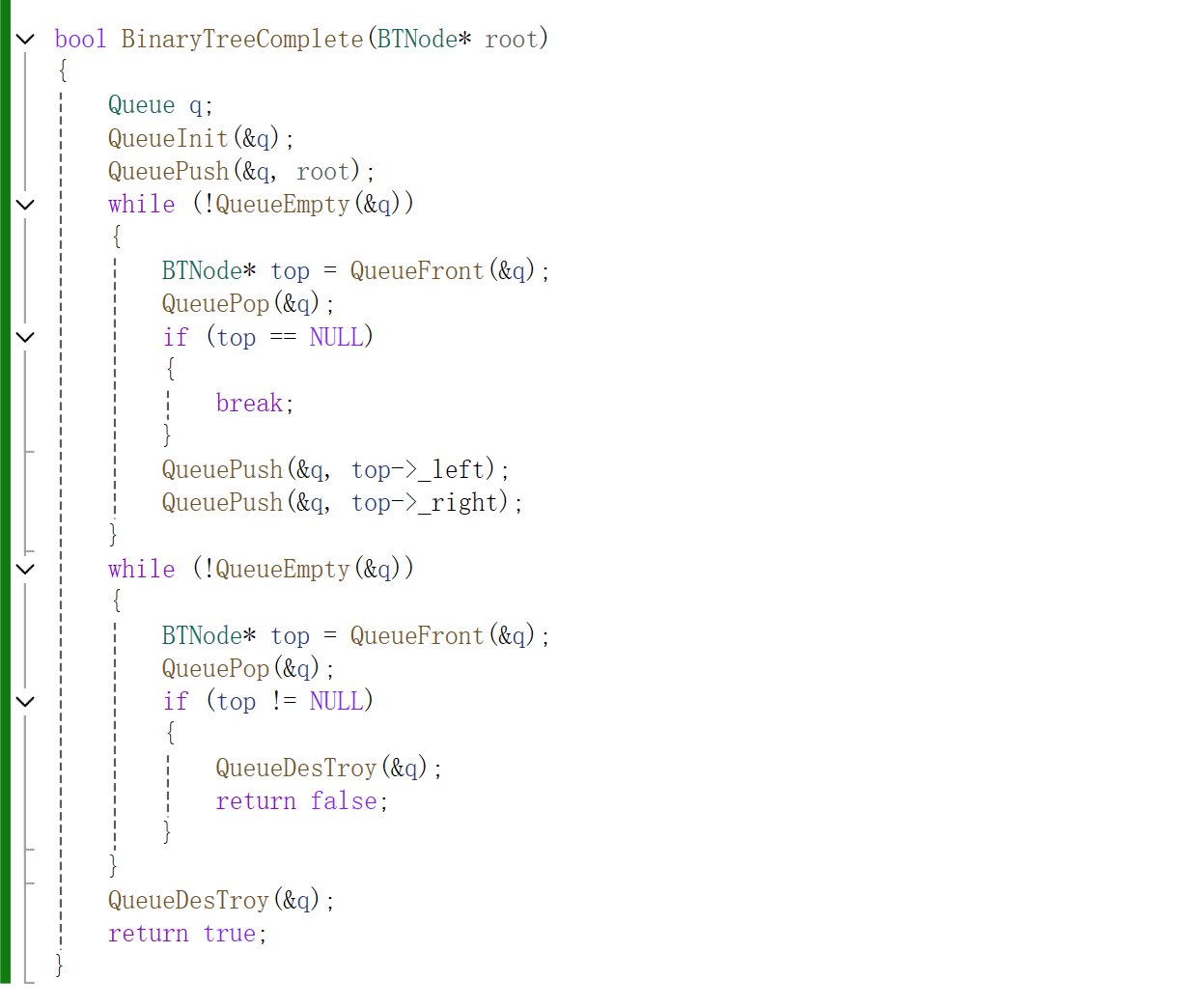
9.判断是否为完全二叉树

利用一个队列，先将root入队，在出root将root左右分别进入队列中，一旦遇到NULL时前面循环跳出，去判断队列中是否有NULL值。如果有不是完全二叉树，若没有则为完全二叉树。

三、代码实现

        1.函数定义

        

        2.函数调用

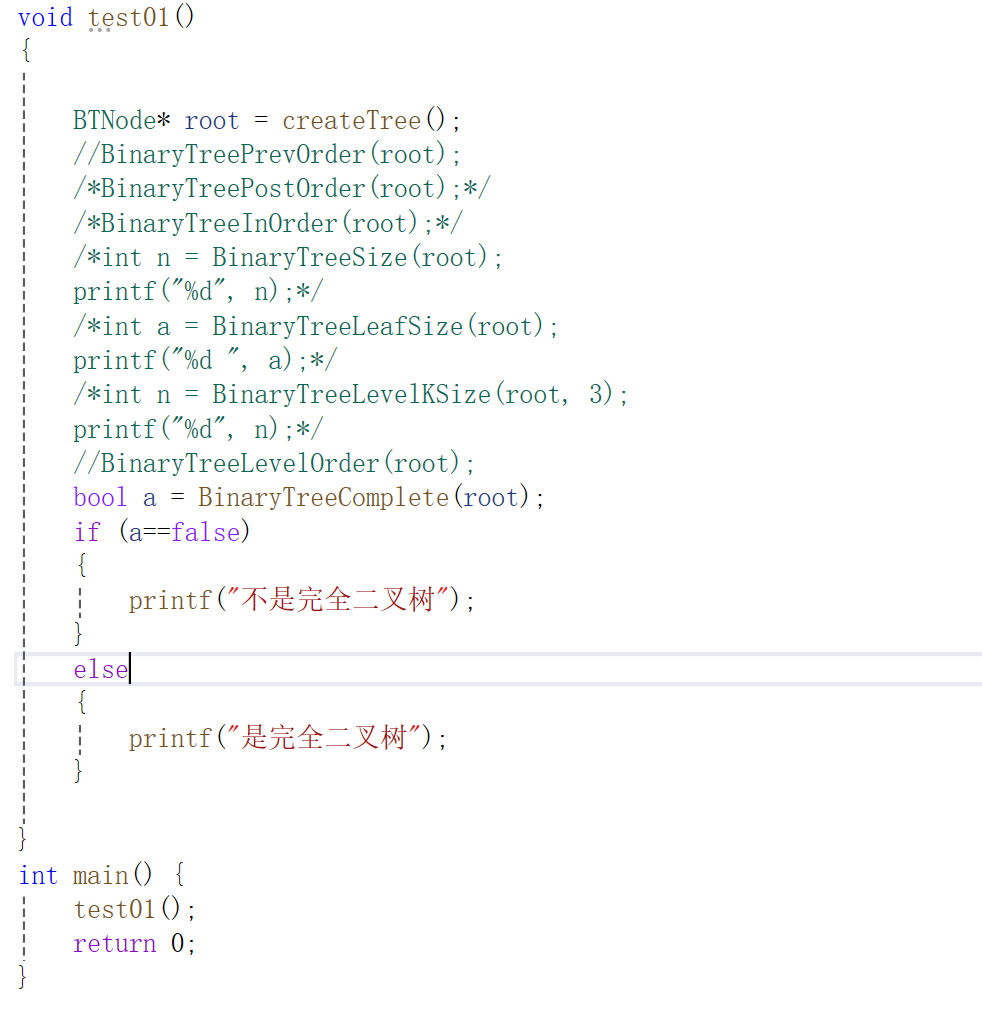
        3.函数功能