堆的实现（C语言版）

一、堆的定义

二、堆的实现

        堆的插入

        堆的删除

        取堆顶数据

        堆的数据个数   

三、堆的代码呈现

        函数定义

        函数调用

        函数实现

一、堆的定义

以二叉树的顺序存储方式来存储元素，堆是一种特殊的二叉树，满足父节点存储数据要大于儿子结点存储数据的一种数据结构，堆分为两种大堆和小堆，大堆是大于儿子结点数据，小堆则是要小于儿子结点数据。如下图所示，图一为小堆，图二为大堆。

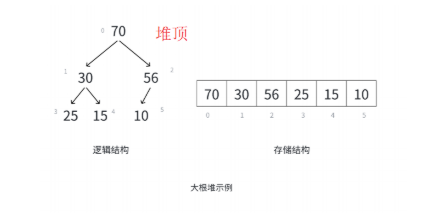
二、堆的实现

        堆的插入

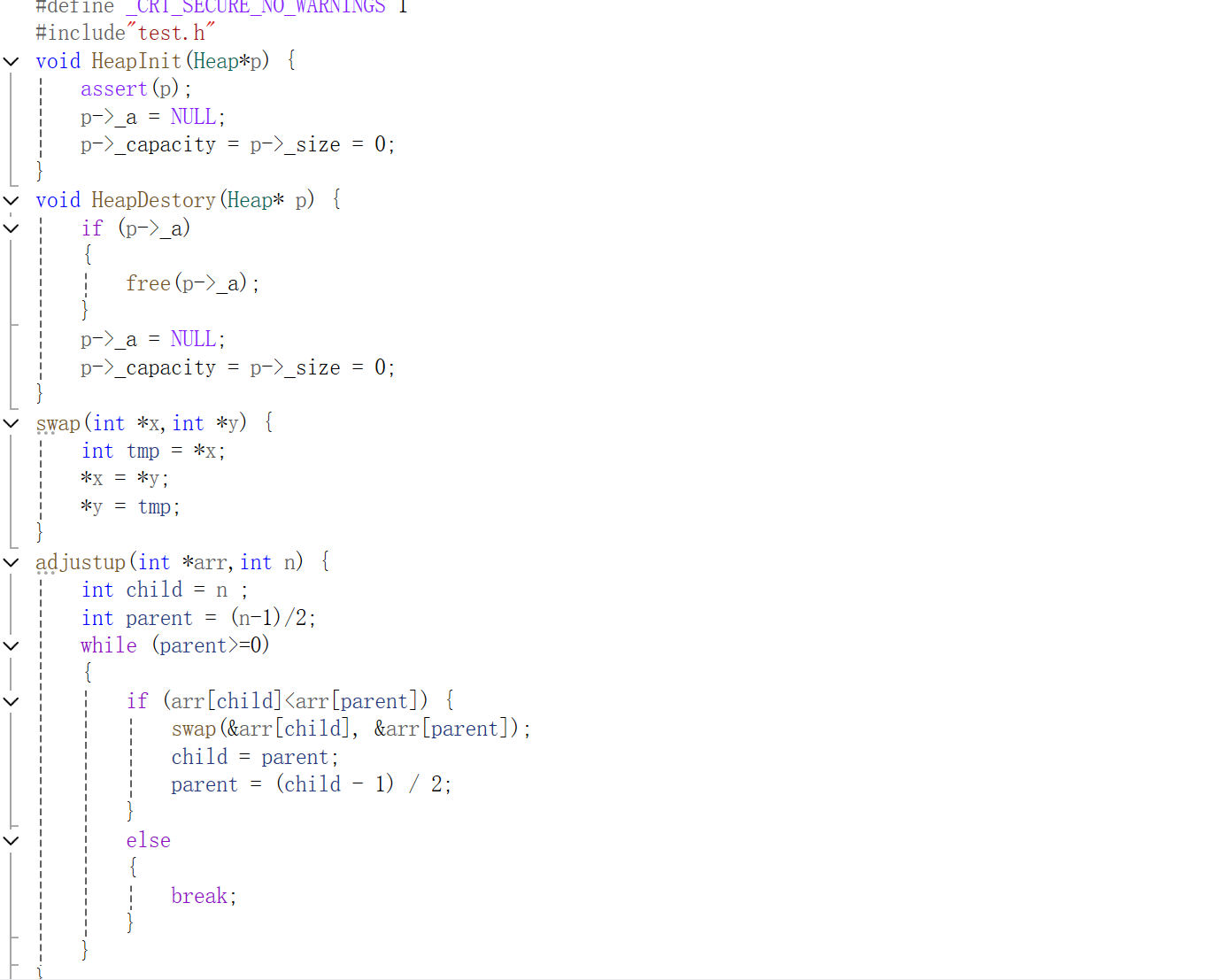
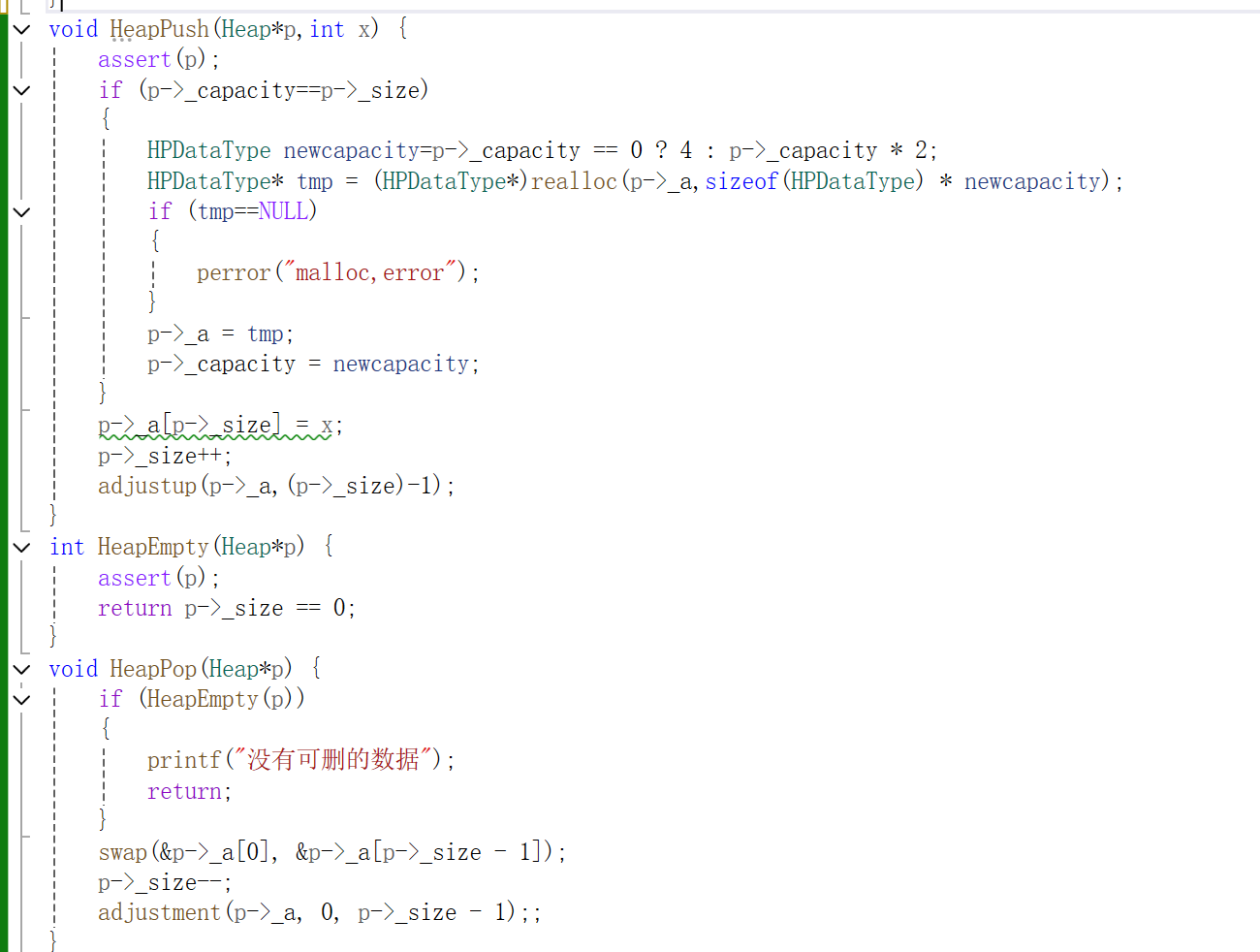
        用线性表先判断其是否有足够的容量，如果没有则需要扩容，扩容后添加要插入的数字。如果按线性表进行添加，不会满足堆的定义，这时我们需要调整，建小堆，需要将最小的值调到堆顶，这时需要向上排序。直接构建一个函数功能向上排序，将最新的线性表下标与数组传入函数中，其中儿子结点是线性表中传入的下标，父亲结点则是儿子节点减一在除以二，用while循环的条件是父节点>=0进入，然后进行判断，如果儿子结点是大于父节点的则不需要交换，直接break，反之则需要交换。如果要构成大堆，直接将排序中小于号改成大于号即可。

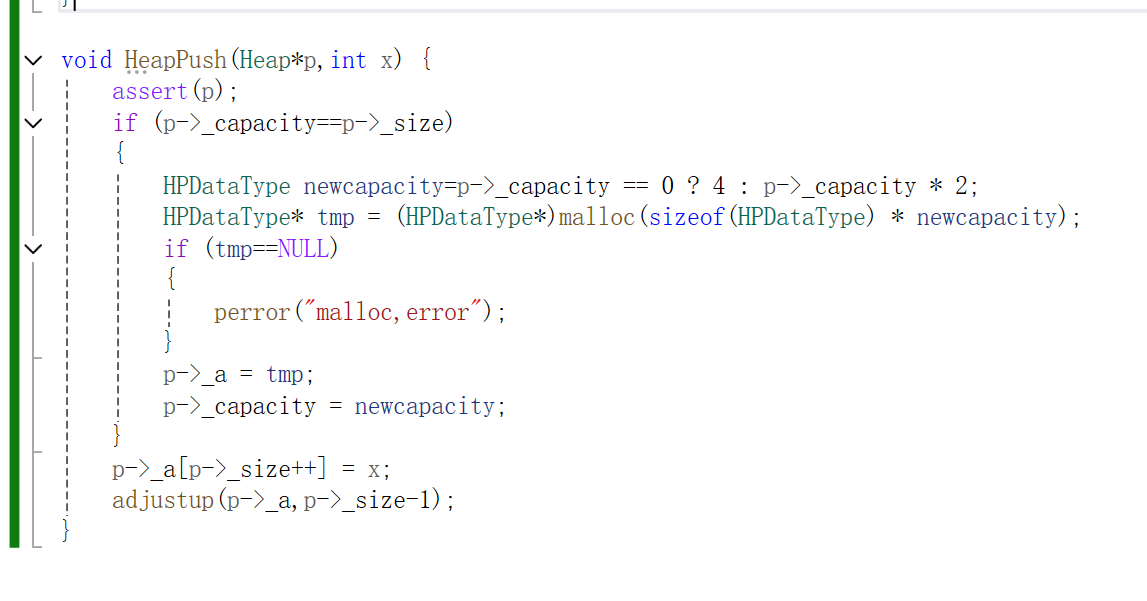
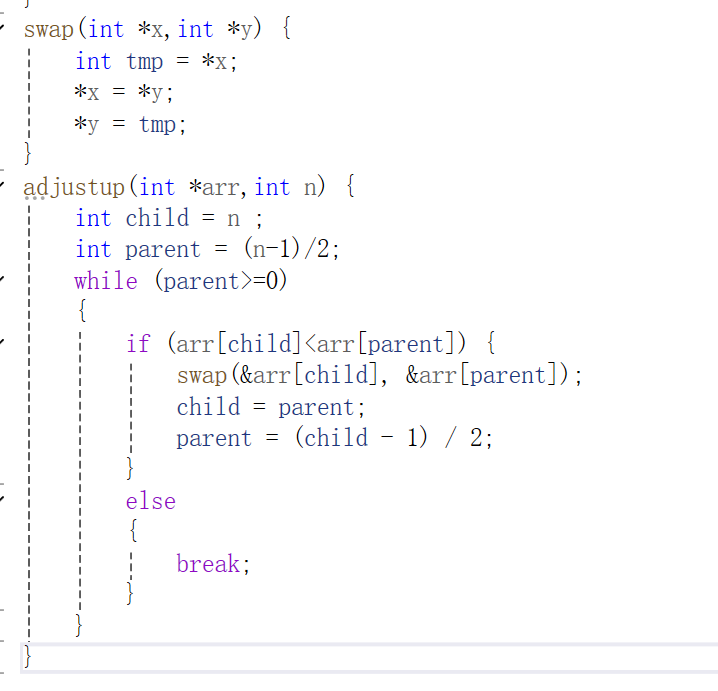
     堆的删除

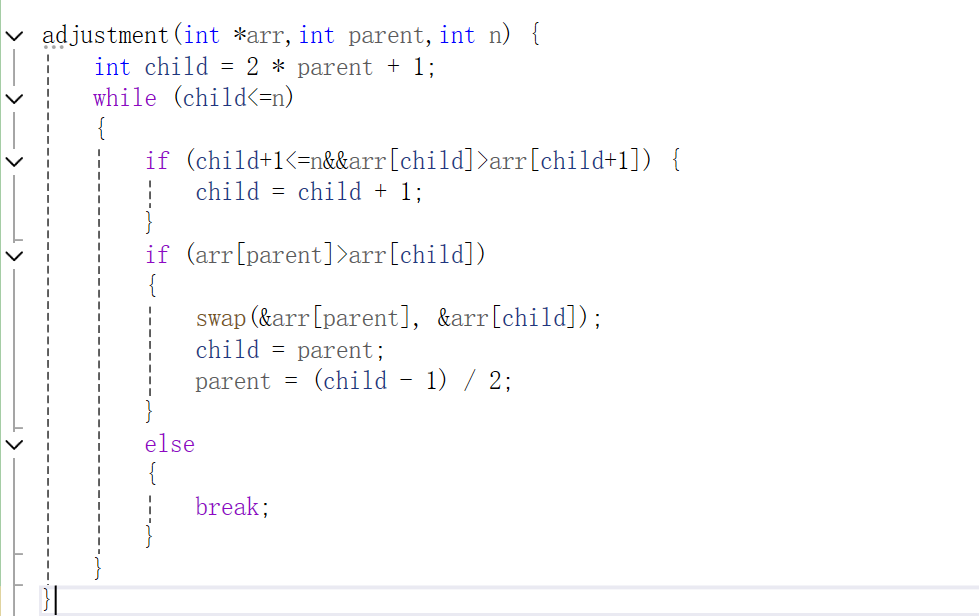
先判断其是否满足删除的条件，条件分别是该指针是否存在或者指针内size的值是否为0.因为堆的删除主要是删除堆顶元素，需要将末尾位置的值和其调换，并且size需要减一，而后经过向下调整重新达到满足小堆的条件。

   

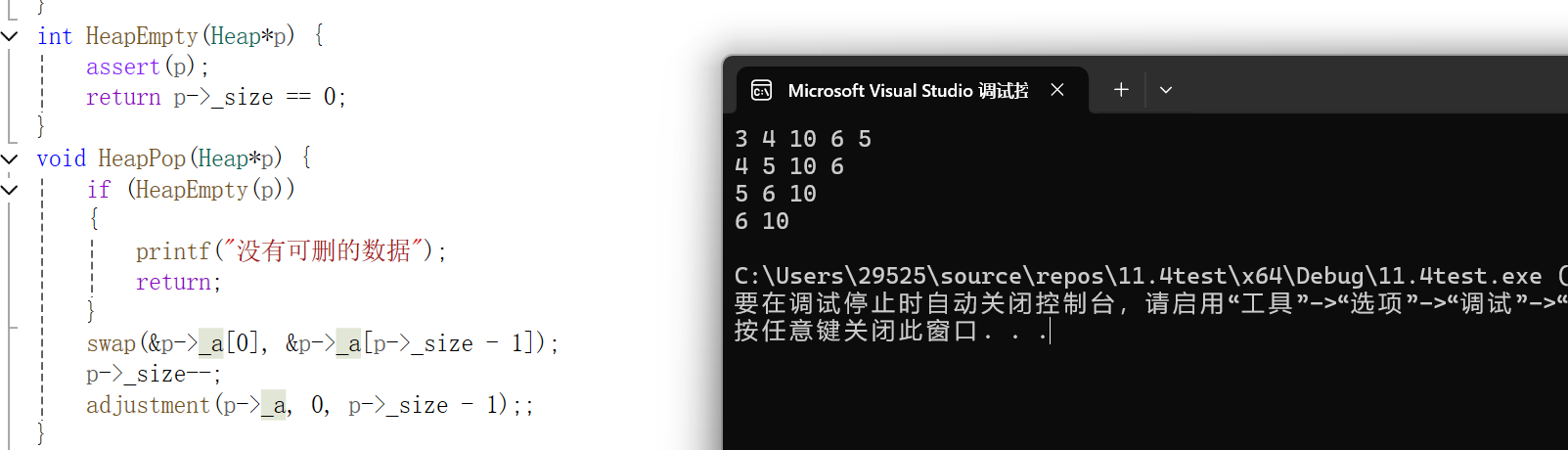
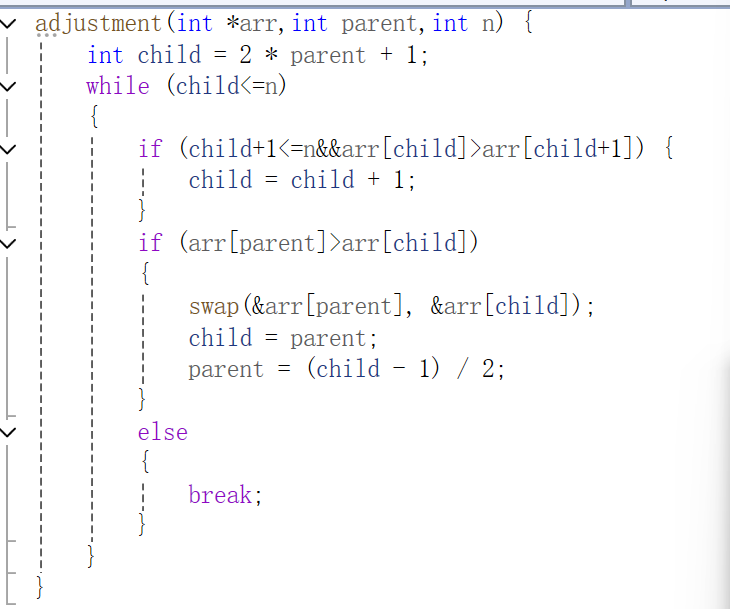
取栈顶数据

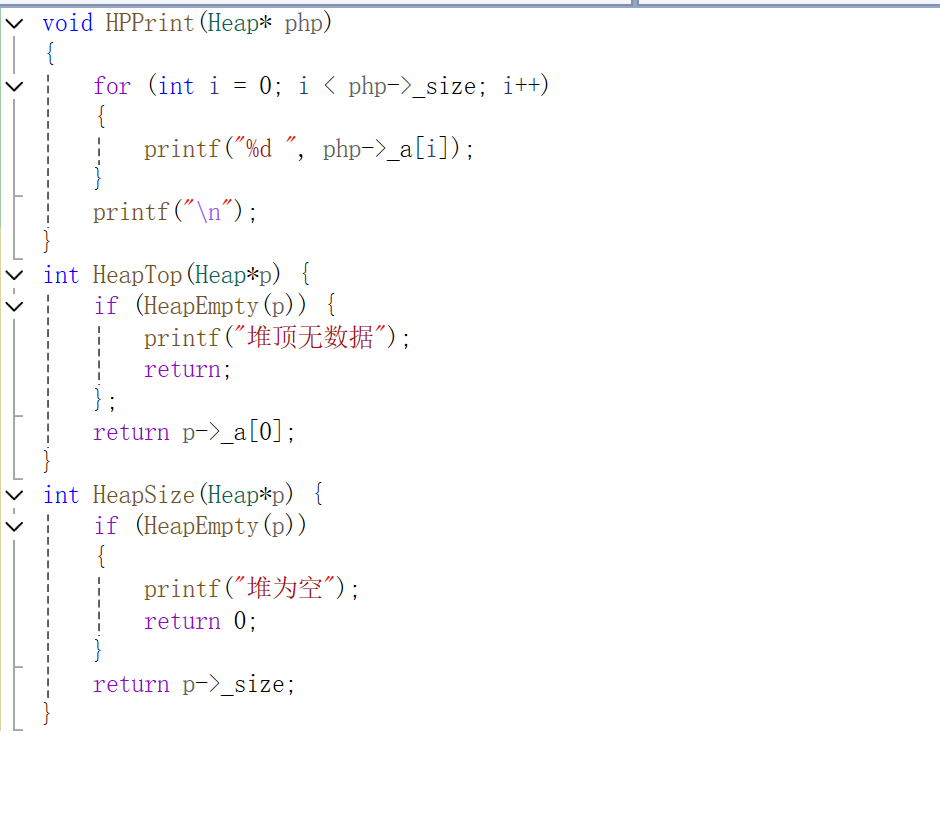
判断是否满足存在栈顶条件，返回下标为0的数据

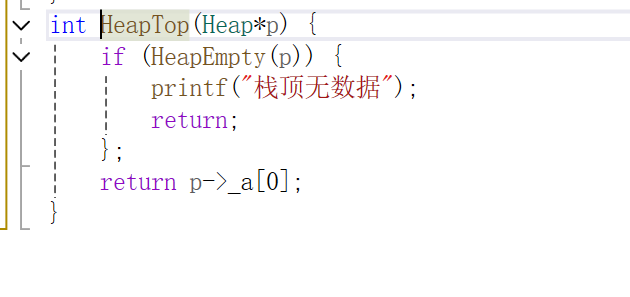
堆的数据个数

直接返回size的大小

三、代码实现

函数定义

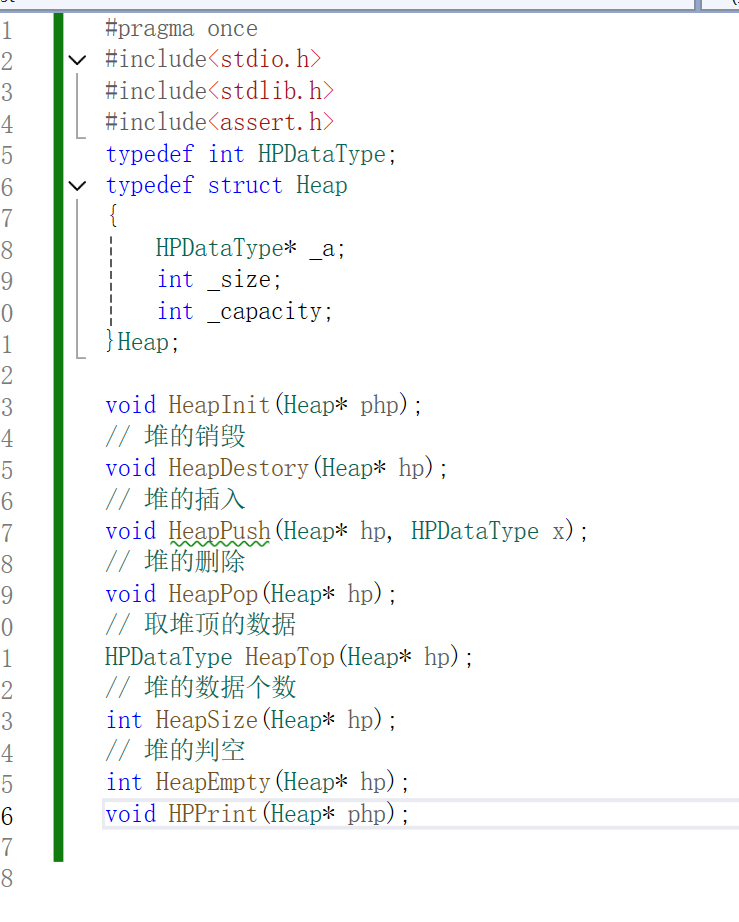
函数调用

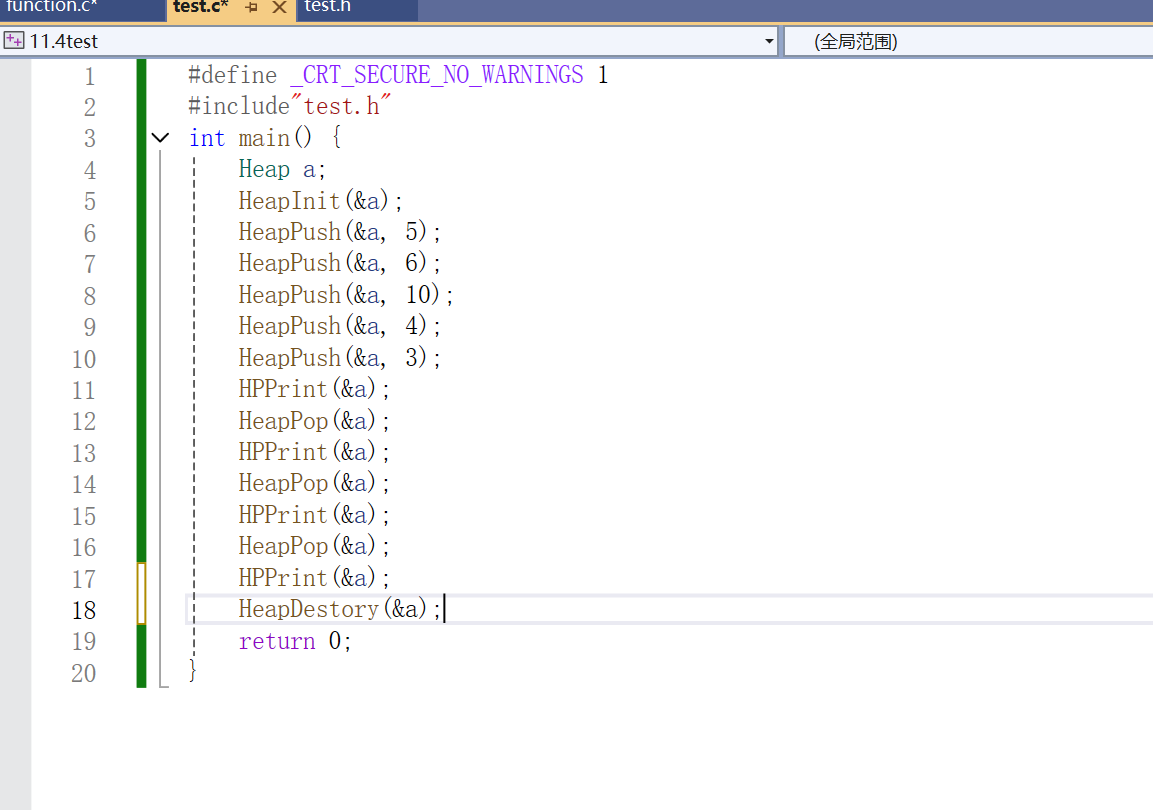
函数实现