leetcode 面试题17.16按摩师

一个有名的按摩师会收到源源不断的预约请求，每个预约都可以选择接或不接。在每次预约服务之间要有休息时间，因此她不能接受相邻的预约。给定一个预约请求序列，替按摩师找到最优的预约集合（总预约时间最长），返回总的分钟数。

注意：本题相对原题稍作改动

示例 1：

输入： [1,2,3,1]
输出： 4
解释： 选择 1 号预约和 3 号预约，总时长 = 1 + 3 = 4。
示例 2：

输入： [2,7,9,3,1]
输出： 12
解释： 选择 1 号预约、 3 号预约和 5 号预约，总时长 = 2 + 9 + 1 = 12。
示例 3：

输入： [2,1,4,5,3,1,1,3]
输出： 12
解释： 选择 1 号预约、 3 号预约、 5 号预约和 8 号预约，总时长 = 2 + 4 + 3 + 3 = 12。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/the-masseuse-lcci

 看到题目的第一眼感觉可以用动态规划做。

方案1

尝试用穷举的方法，递归列举所有可能性，然后求其中最大值。

通过分析题目我们可以直到按摩师不可以接受了紧挨的两个预约，因此他每一次有两个选择：

1. 接受当前预约

2. 拒绝当前预约

所以需要从这两种情况中挑出最大值，然后继续进行进行选择，直到最后选择完毕。

int[] ns; //全局变量

public int massage(int[] nums) {
    if(nums.length == 0) return 0;
    ns = nums;
    return f(ns.length-1);
}

// 递归
public int f(int i){
    if(i==0) // 递归出口
        return ns[0];
    else if(i==1) 
        return Math.max(ns[0], ns[1]);
    // 从两种情况中选出值大的一种
    return Math.max(f(i - 1), ns[i] + f(i - 2));
}

分析

这个方案可以解决这个问题，但是要频繁的进行递归操作，而且其中也有大量的重复运算。

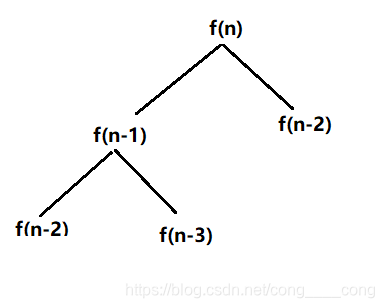
所以可以对重复的计算进行记忆处理。

方案2

对方案1进行改进，增加记忆数组，减少不必要的计算过程。

int[] ns;
int[] memery;

public int massage(int[] nums) {
    if(nums.length == 0) return 0;
    ns = nums;
    memery = new int[ns.length];
    //标识状态为-1
    for (int i = 0; i < memery.length ; i++) {
        memery[i] = -1;
    }
    return f2(ns.length-1);
}

// 递归改进记忆
public int f2(int i){
    if(i==0)
        return ns[0];
    else if(i==1)
        return Math.max(ns[0], ns[1]);
    else if(memery[i] != -1)
        return memery[i];
    else
        memery[i] = Math.max(f(i-1), ns[i]+f(i-2));
    return memery[i];
}

分析

改进后的算法相比之前性能有了很大的提升，时间复杂度O(N)，空间复杂度也是 O(N)

方案3

利用动态规划。设一个数组dp，长度和nums一样即可。

dp[i] 表示在 i 时刻，接受预约的时间最长，可以通过 i-1 时刻和当前时刻加上 i-2 时刻中最大值获取。

dp[i] = max(dp[i-1], nums[i] + dp[i-2])

默认dp[0]= nums[0]，dp[1] = max(nums[0], nums[1])

// 动态规划
public int massage(int[] nums){
    if(nums.length == 0){
        return 0;
    }else if(nums.length == 1){
        return nums[0];
    }
    int[] dp = new int[nums.length];
    dp[0] = nums[0];
    dp[1] = nums[0] > nums[1] ? nums[0] : nums[1];
    for (int i = 2; i < dp.length; i++) {
        dp[i] = Math.max(dp[i-1], nums[i] + dp[i-2]);
    }
    return dp[nums.length-1];
}

分析

动态规划算法不需要使用递归，只需要进行一次遍历即可得到答案，相比递归代码需要频繁的进行入栈和出栈操作，还是有优势的。