树概念及二叉树

树的表示三种方法

1、双亲表示法

假设以一组连续空间存储树的结点，同时在每个结点中附设一个指示器指示其双亲结点在链表中的位置,其形式说明如下:


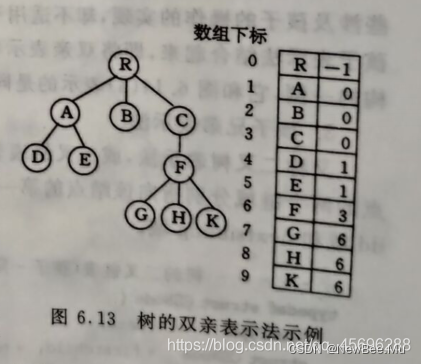
这种存储结构利用了每个结点(除根以外)只有惟一的双亲的性质。PARENT(T,x)操作可以在常量时间内实现。反复调用PARENT操作，直到遇见无双亲的结点时，便找到了树的根,这就是ROOT(x)操作的执行过程。但是，在这种表示法中,求结点的孩子时需要遍历整个结构

2、孩子表示法

由于树中每个结点可能有多棵子树，则可用多重链表，即每个结点有多个指针域，其中每个指针指向一棵子树的根结点，此时链表中的结点可以有如下两种结点格式。

若采用第一种结点格式，则多重链表中的结点是同构的，其中d为树的度。由于树中很多结点的度小于d，所以链表中有很多空链域，空间较浪费，不难推出，在一棵有n个结点度为k的树中必有n(k-1)+1个空链域。若采用第二种结点格式，则多重链表中的结点是不同构的，其中J为结点的度，degre域的值同J。此时，虽能节约存储空间，但操作不方便。

另一种办法是把每 个结点的孩子结点排列起来 ,看成是一个线性表，且以单链表作存储结构，则n个结点有n个孩子链表(叶子的孩子链表为空表)。而n个头指针又组成一个线性表，为了便于查找，可采用顺序存储结构。这种存储结构可形式地说明如下:

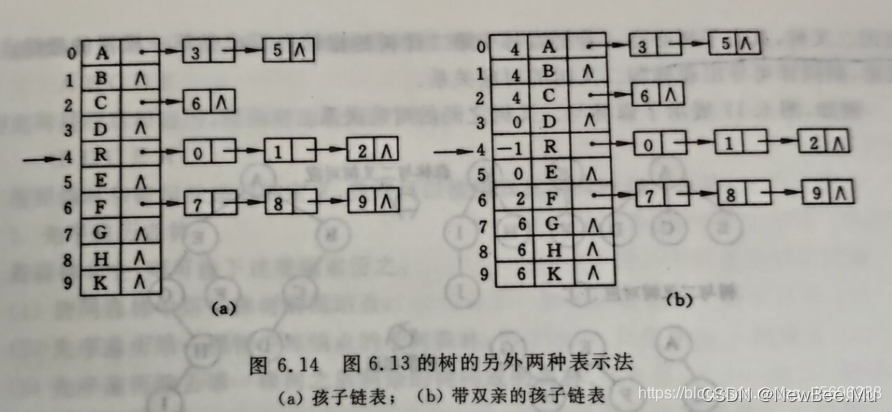
图6.14(a)是图6.13中的树的孩子表示法。与双亲表示法相反，孩子表示法便于那些涉及孩子的操作的实现，却不适用于PARENT(T,x)操作，我们可以把双亲表示法和孩子表示法结合起来，即将双亲表示和孩子链表合在一起。图6.14(b)就是这种存储结构的一例，它和图6.14(a)表示的是同一棵树。

3、孩子兄弟表示法 （相当于前面讲的将一颗树转换成一颗二叉树）

又称二叉树表示法，或二又链表表示法，即以二又链表作树的存储树的存储结构。链表中结点的两个链城分别指向该结点的第一个孩子结点和下一个兄弟结点，分别命名为firstchild城和nextsibling城。


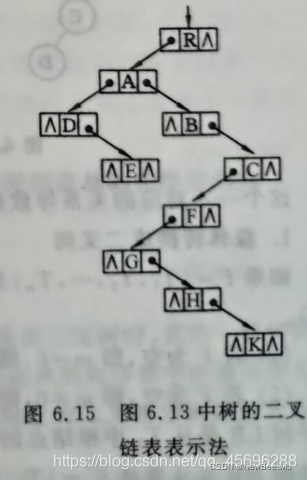
图6.15是图6.13中的树的孩子兄弟链表。利用这种存储结构便于实现各种树的操作。首先易于实现找结点孩子等的操作。例如:若要访问结点x的第i个孩子，则只要先从firstchild域找到第1个孩子结点，然后沿着孩子结点的nextsibling域连续走i-1步，便可找到x的第i个孩子。当然，如果为每个结点增设一个PARENT域，则同样能方便地实现PARENT(T,x)操作。

一、二叉树的四种遍历方式

先序遍历：A → B → D → C
中序遍历：B → D → A → C
后续遍历：D → B → C → A
层序遍历：A → B → C → D
先序、中序、后序其实指的是父节点被访问的次序。若在遍历过程中，父节点先于它的子节点被访问，就是先序遍历；父节点被访问的次序位于左右孩子节点之间，就是中序遍历；访问完左右孩子节点之后再访问父节点，就是后序遍历。不论是先序遍历、中序遍历还是后序遍历，左右孩子节点的相对访问次序是不变的，总是先访问左孩子节点，再访问右孩子节点。而层次遍历，就是按照从上到下、从左向右的顺序访问二叉树的每个节点。

package test;

import java.util.LinkedList;  
import java.util.List;  
  
/** 
 * 功能：把一个数组的值存入二叉树中，然后进行3种方式的遍历 
 *  
 * @author huapro @date: 2022-02-21 
 *  
 */  
public class BinTreeTraverse2 {  
  
    private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };  
    private static List<Node> nodeList = null;  
  
    /** 
     * 内部类：节点 
     *  
     * @author ocaicai@yeah.net @date: 2011-5-17 
     *  
     */  
    private static class Node {  
        Node leftChild;  
        Node rightChild;  
        int data;  
  
        Node(int newData) {  
            leftChild = null;  
            rightChild = null;  
            data = newData;  
        }  
    }  
  
    public void createBinTree() {  
        nodeList = new LinkedList<Node>();  
        // 将一个数组的值依次转换为Node节点  
        for (int nodeIndex = 0; nodeIndex < array.length; nodeIndex++) {  
            nodeList.add(new Node(array[nodeIndex]));  
        }  
        // 对前lastParentIndex-1个父节点按照父节点与孩子节点的数字关系建立二叉树  
        for (int parentIndex = 0; parentIndex < array.length / 2 - 1; parentIndex++) {  
            // 左孩子  
            nodeList.get(parentIndex).leftChild = nodeList.get(parentIndex * 2 + 1);  
            // 右孩子  
            nodeList.get(parentIndex).rightChild = nodeList.get(parentIndex * 2 + 2);
        }  
        // 最后一个父节点:因为最后一个父节点可能没有右孩子，所以单独拿出来处理  
        int lastParentIndex = array.length / 2 - 1;  
        // 左孩子  
        nodeList.get(lastParentIndex).leftChild = nodeList  
                .get(lastParentIndex * 2 + 1);  
        // 右孩子,如果数组的长度为奇数才建立右孩子  
        if (array.length % 2 == 1) {  
            nodeList.get(lastParentIndex).rightChild = nodeList  
                    .get(lastParentIndex * 2 + 2);  
        }  
    }  
  
    /** 
     * 先序遍历 
     * 这三种不同的遍历结构都是一样的，只是先后顺序不一样而已 
     * @param node 
     * 遍历的节点 
     */  
    public static void preOrderTraverse(Node node) {  
        if (node == null)  
            return;  
        System.out.print(node.data + " ");  
        preOrderTraverse(node.leftChild);  
        preOrderTraverse(node.rightChild);  
    }  
  
    /** 
     * 中序遍历 
     * 这三种不同的遍历结构都是一样的，只是先后顺序不一样而已 
     * @param node 
     * 遍历的节点 
     */  
    public static void inOrderTraverse(Node node) {  
        if (node == null)  
            return;  
        inOrderTraverse(node.leftChild);  
        System.out.print(node.data + " ");  
        inOrderTraverse(node.rightChild);  
    }  
  
    /** 
     * 后序遍历 
     * 这三种不同的遍历结构都是一样的，只是先后顺序不一样而已 
     * @param node 
     * 遍历的节点 
     */  
    public static void postOrderTraverse(Node node) {  
        if (node == null)  
            return;  
        postOrderTraverse(node.leftChild);  
        postOrderTraverse(node.rightChild);  
        System.out.print(node.data + " ");  
    }  
  
    public static void main(String[] args) {  
        BinTreeTraverse2 binTree = new BinTreeTraverse2();  
        binTree.createBinTree();  
        // nodeList中第0个索引处的值即为根节点  
        Node root = nodeList.get(0);  
  
        System.out.println("先序遍历：");  
        preOrderTraverse(root);  
        System.out.println();  
  
        System.out.println("中序遍历：");  
        inOrderTraverse(root);  
        System.out.println();  
  
        System.out.println("后序遍历：");  
        postOrderTraverse(root);  
    }  
}

二、几种特殊的二叉树

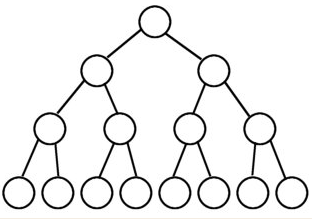
1、满二叉树

所有叶结点同处于最底层（非底层结点均是内部结点），一个深度为k(>=-1)且有2^(k+1) - 1个结点(满二叉树可以为空)。

2、完全二叉树

**叶结点只能出现在最底层的两层，且最底层叶结点均处于次底层叶结点的左侧。**规模为n的完全二叉树，高度为

3、平衡二叉树

平衡二叉树（Self-balancing binary search tree）又被称为AVL树（有别于AVL算法，AVL 树是一种平衡二叉树,得名于其发明者的名字( Adelson-Velskii 以及 Landis)），且具有以下性质：它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci(斐波那契)数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。
对于平衡二叉树要特别注意的是，不要求非叶节点都有两个子结点，仅要求两个子树的高度差的绝对值不超过1，或者为空树。

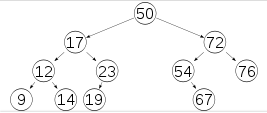
三、存储方式

存储的方式和图一样，有链表和数组两种，用数组存访问速度快，但插入、删除节点操作就比较费时了。实际中更多的是用链来表示二叉树的。