简单重温快速排序法（QuickSort）

更多算法，请我的网站：http://www.comiscience.com

 

In-place 的快排方法。

 

例子 ：

 

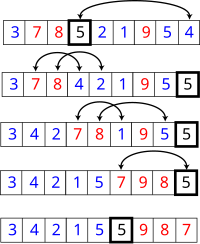
原始序列数： 3 7 8 5 2 1 9 5 4

 

1、选取中间的5，将5与最后的4互掉位置，生成新的序列：

     3 7 8 4 2 1 9 5  5

2、我们把比上面5 小的数集中排到比5 大的数的前面，我们使用最快地方法：

• 从第一个元素3和最后一个元素5 比较，发现3小于5，则用3和3互换，但发现是同一元素，所以不动，序列不变。
• 拿第2个元素7和5 比较，发现7大于5 ，则7不变。
• 拿第3个元素8和5 比较，发现仍然大于，则8不变。
• 拿第4个元素4和5 比较，发现小于5 ，则4和7交换位置，序列变为了：3 4 8 7 2 1 9 5  5
• 拿第5个元素2和5 比较，发现小于5 ，则2和8交换位置，序列变为了：3 4 2 7 8 1 9 5  5
• 拿第6个元素1和5 比较，发现小于5 ，则1和7交换位置，序列变为了：3 4 2 1 8 7 9 5 5
• 拿第7个元素9和5 比较，发现大于5 ，则9不变。
• 拿第8个元素5和5 比较，发现相同，则新的序列变为：3 4 2 1 5 7 9 8 5
• 从头到尾对比一遍之后，我们把 5 和7兑换位置，新的序列变为： 3 4 2 1 5  5   9 8 7 

 

 

     如图所示 

 

    到此为止，5 左边的数都小于它，右面的数都大于它。

 

3、我们将上面5左右两边的序列分开，作序列为3 4 2 1 5 右序列为9 8 7。我们对这左右两个序列重复上面1、2部的操作。我们可以得到如下序列：

    左序列： 1  2   4 5 3    右序列：7  8   9

4、我们再次重复1、2步的操作，将第3步后的新的分序列排序：序列1: 1  ； 序列2: 4 5 3  ； 序列3: 7  ； 序列4:  9；

5、按照1、2、3步骤，我们逐步的对子序列排序，最后我们得到排序后的最终序列  1 2 3 4 5 5 7 8 9

 

 

算法：

 

上面的过程如果不是很明白，我们看下面的算法。上面的例子中，选取重点 标示的数字都是随机选择的，看下面的算法尽量理解。

 

 

 //快排主程序 //a不规则的数据的序列，left序列中最左变得元素，right序列中最右面的元素， pivotindex从序列中随机抽取的作为分隔序列的轴元素的位置 void quicksort(a, left, right) { if(right > left) { select a pivot value a[pivotIndex]//随机从序列a中选一个轴pivot pivotNewIndex = partition(a, left, right, pivotIndex); quicksort(a, left, pivotNexindex-1); quicksort(a, pivotNewIndex+1, right); } }

 

 

//该函数将一个序列分为两部分，pivotIndex位置的元素左边的元素都是小于等于pivotIndex元素的，pivotIndex位置右面的元素都是大于pivotIndex元素的，storeIndex记录着最后轴元素应该在的位置。 void partition(a, left, right, pivotIndex) { pivotValue = a[pivotIndex]; swap(a[pivotIndex],a[right]);//把pivot移到结尾 storeIndex = left; for(int i=left;i<right;i++) { if(a[i]<pivotValue) { swap(a[sotreIndex],a[i]); storeIndex=sotreIndex+1; } } swap(a[right],a[storeIndex]);//把pivot移到storeIndex的位置 return storeIndex; }

 

时间复杂度：

平均为：O(n   log  n )

最糟情况为： O (n² )

 

这个不能想象，假设每个序列都分为两个序列，一直到每个序列都只有1个元素的时候，这个的复杂度是 log  n

每次分序列后，从新排列的元素，就是从左到有的所有元素，是n

每次为n，一共有 log  n 次，那时间复杂度就是 O(n   log  n )

 

最早情况也很容易，假设一个序列有8个元素，每次运行函数 partition之后，总是有一个序列里只有一个元素，那么相当于我们一共分了n次，每次要排n个元素，所以最后是n*n。

 

如果大家看不懂，我下面引用wiki的台湾人的原话：

 

從一開始快速排序平均需要花費O(n log n)時間的描述並不明顯。但是不難觀察到的是分割運算，陣列的元素都會在每次迴圈中走訪過一次，使用Θ(n)的時間。在使用結合（concatenation）的版本中，這項運算也是Θ(n)。 在最好的情況，每次我們執行一次分割，我們會把一個數列分為兩個幾近相等的片段。這個意思就是每次遞迴呼叫處理一半大小的數列。因此，在到達大小為一的數列前，我們只要作 log n 次巢狀的呼叫。這個意思就是呼叫樹的深度是O(log n)。但是在同一階層的兩個程序呼叫中，不會處理到原來數列的相同部份；因此，程序呼叫的每一階層總共全部僅需要O(n)的時間（每個呼叫有某些共同的額外耗費，但是因為在每一階層僅僅只有O(n)個呼叫，這些被歸納在O(n)係數中）。結果是這個演算法僅需使用O(n log n)時間。 另外一個方法是為T(n)設立一個遞迴關係式，也就是需要排序大小為n的數列所需要的時間。在最好的情況下，因為一個單獨的快速排序呼叫牽涉了O(n)的工作，加上對n/2大小之數列的兩個遞迴呼叫，這個關係式可以是： T(n) = O(n) + 2T(n/2) 解決這種關係式型態的標準数学归纳法技巧告訴我們T(n) = Θ(n log n)。 事實上，並不需要把數列如此精確地分割；即使如果每個基準值將元素分開為 99% 在一邊和 1% 在另一邊，呼叫的深度仍然限制在 100log n，所以全部執行時間依然是O(n log n)。 然而，在最壞的情況是，兩子數列擁有大各為 1 和 n-1，且呼叫樹（call tree）變成為一個 n 個巢狀（nested）呼叫的線性連串（chain）。第 i 次呼叫作了O(n-i)的工作量，且遞迴關係式為： T(n) = O(n) + T(1) + T(n - 1) = O(n) + T(n - 1) 這與插入排序和选择排序有相同的關係式，以及它被解為T(n) = Θ(n2)。