数独C++代码实现

数独是源自18世纪瑞士的一种数学游戏。中文中“数独”一次，实际上是源自于日语对于数独的音译。是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫（3*3）内的数字均含1-9，不重复。
一个标准的9x9数独如下所示（当然还可以有更复杂的变体）

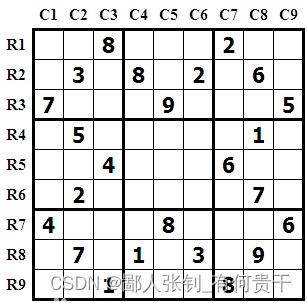
你需要根据上述规则将其填满

对于人类来说最容易的方法是排除法，但如果让我用程序去解决的话最容易想到使用回溯法。

问题定义：我们使用9x9的二维vector装载数据，原始数据中有数字的填数字，没有的填'.'（或者其他）。我们使用char类型存储，因为我们其实只需要十个值。我们的目标就是将'.'全部变成数字，并且符合数独的游戏规则。

bool backtracking(vector<vector<char>>& board) {
    for (int i = 0; i < board.size(); i++) {         // 遍历行
        for (int j = 0; j < board[0].size(); j++) { // 遍历列
            if (board[i][j] != '.') continue;           // 如果该位置已经被填写，则过这一次填写
            for (char k = '1'; k <= '9'; k++) {     // (i, j) 这个位置放k是否合适
                if (isValid(i, j, k, board)) {             // 是否有某行或者某列或者小宫格中有重复数字
                    board[i][j] = k;                        // 如果有效则放置k
                    if (backtracking(board)) return true; // 递归填下个数字，只有当最后一个数字都合适的时候才会返回true，否则返回false。
                    board[i][j] = '.';                       // 不合适则撤销k
                }
            }
            return false;                                   // 9个数都试完了，都不行，那么就返回false
        }
    }
    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
    for (int i = 0; i < 9; i++) {    // 判断行里是否重复
        if (board[row][i] == val) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) {    // 判断列里是否重复
        if (board[j][col] == val) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) {    // 判断9方格里是否重复
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val ) {
                return false;
            }
        }
    }
    return true;
}

转载请标明出处，原文地址：鄙人张钊_有何贵干_物联网,C/C++,深度学习-优快云博客