文章目录
- 全概率公式和贝叶斯公式
- 均匀分布变换定理
- F(x,y)与f(x,y)
- 已知 F ( x , y ) F(x,y) F(x,y),如何求 f ( x , y ) f(x,y) f(x,y)?
- 已知 F ( x , y ) F(x,y) F(x,y),如何求 F Y ( y ) F_Y(y) FY(y)和 F X ( x ) F_X(x) FX(x)、 f Y ( y ) f_Y(y) fY(y)和 f X ( x ) f_X(x) fX(x)?
- 已知 F ( x , y ) F(x,y) F(x,y),如何求 F X ∣ Y ( x ∣ y ) F_{X|Y}(x|y) FX∣Y(x∣y)、 f X ∣ Y ( x ∣ y ) f_{X|Y}(x|y) fX∣Y(x∣y)?
- 独立和不相关之间的关系
- 如何判断两个随机变量是否独立?
- 亚当夏娃公式
- 常见分布及其期望方差
- 如果随机变量X和Y相互独立,分别都服从泊松分布,请问X+Y是否服从泊松分布?
- 已知 X i ∼ N ( μ , σ 2 ) X_i \sim N(\mu,\sigma^2) Xi∼N(μ,σ2),为什么 ∑ i = 1 n ( X i − X ˉ ) 2 σ 2 ∼ χ 2 ( n − 1 ) \frac{\sum_{i=1}^{n}(X_i-\bar{X})^2}{\sigma^2} \sim \chi^2(n-1) σ2∑i=1n(Xi−Xˉ)2∼χ2(n−1)?
- 为什么 S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2 S2=n−11∑i=1n(Xi−Xˉ)2,而不是 1 n ∑ i = 1 n ( X i − X ˉ ) 2 \frac{1}{n}\sum_{i=1}^{n}(X_i-\bar{X})^2 n1∑i=1n(Xi−Xˉ)2
- E ( 2 X ) = ? 2 E [ X ] . E(2^X)\; \overset{?}{=}\; 2^{E[X]}. E(2X)=?2E[X].
- 已知随机变量X和Y都服从标准正态分布,且X和Y相互独立,求 Z = X 2 + Y 2 Z = X^2 + Y^2 Z=X2+Y2 的概率分布
- 统计量
- 伽马函数
- 切比雪夫不等式
- 柯西-施瓦茨不等式
- 什么是柯西施瓦茨不等式?
- 为什么相关系数的绝对值一定小于等于1?(为什么 Cov 2 ( X , Y ) ≤ Cov ( X , X ) Cov ( Y , Y ) \text{Cov}^2(X,Y) ≤ \text{Cov}(X,X)\text{Cov}(Y,Y) Cov2(X,Y)≤Cov(X,X)Cov(Y,Y))
- 为什么 E 2 ( X Y ) ≤ E ( X 2 ) E ( Y 2 ) E^2(XY) \leq E(X^2)E(Y^2) E2(XY)≤E(X2)E(Y2)?
- 为什么平方的期望大于等于期望的平方?
- 为什么 E ( ∣ X ∣ ) ≤ E ( X 2 ) E(|X|) \leq \sqrt{E(X^2)} E(∣X∣)≤E(X2)?
- Jensen 不等式
- 大数定律
- 中心极限定理
- 常见统计量及其分布
- 区间估计
- 如何求假设检验过程中的拒绝域
- 拒绝域、显著性水平、置信水平之间的关系
- 薄弱点实时统计
全概率公式和贝叶斯公式
我们知道不同的原因可能导致同一种结果(比如你家里没电了,可能是你用大功率电器导致跳闸了,也可能是外面的电缆断了)。
贝叶斯公式解决的核心问题就是:在已知某种问题发生的情况下,求导致这个结果的各种原因发生的概率(比如你家停电了,有1/3的可能是外面电缆断了,还有2/3的可能是你自己用大功率电器烧了)
下面是贝叶斯公式的定义

是不是感觉很绕,下面我给你写个容易看懂的
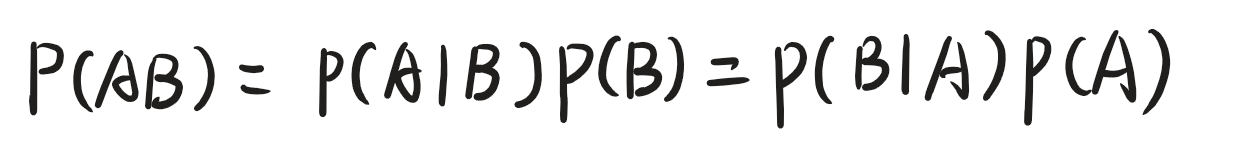
这个其实就是贝叶斯公式的核心思想,不信你自己推推
均匀分布变换定理
核心结论:若X的分布函数F(x)严格单调递增且连续,则 Y = F ( X ) 服从 U ( 0 , 1 ) Y=F(X)服从~U(0,1) Y=F(X)服从 U(0,1)
证明核心思路
要证明Y服从[0,1]上的均匀分布,只需证明Y的分布函数G(y)满足:
- 当 y < 0 y<0 y<0时, G ( y ) = 0 G(y)=0 G(y)=0;
- 当 0 ≤ y ≤ 1 0≤y≤1 0≤y≤1时, G ( y ) = y G(y)=y G(y)=y;
- 当 y > 1 时 y>1时 y>1时, G ( y ) = 1 G(y)=1 G(y)=1。
分步证明过程
-
定义Y的分布函数
G ( y ) = P ( Y ≤ y ) = P ( F ( X ) ≤ y ) G(y) = P(Y ≤ y) = P(F(X) ≤ y) G(y)=P(Y≤y)=P(F(X)≤y),这是分布函数的基本定义 -
分情况讨论 G ( y ) G(y) G(y)的取值
- 当 y < 0 y < 0 y<0时: F ( X ) F(X) F(X)是分布函数,取值范围始终在 [ 0 , 1 ] [0,1] [0,1]内,故 P ( F ( X ) ≤ y ) = 0 P(F(X) ≤ y)=0 P(F(X)≤y)=0,即 G ( y ) = 0 G(y)=0 G(y)=0
- 当 y > 1 y > 1 y>1时:同理, F ( X ) ≤ 1 F(X)≤1 F(X)≤1恒成立,故 P ( F ( X ) ≤ y ) = 1 P(F(X) ≤ y)=1 P(F(X)≤y)=1,即 G ( y ) = 1 G(y)=1 G(y)=1
- 当 0 ≤ y ≤ 1 0 ≤ y ≤ 1 0≤y≤1时:因F(x)严格单调递增且连续,存在唯一逆函数F⁻¹(y)
- 由“严格单调递增函数的不等式等价性”, F ( X ) ≤ y F(X) ≤ y F(X)≤y 等价于 X ≤ F − 1 ( y ) X ≤ F⁻¹(y) X≤F−1(y)
- 代入分布函数定义得: P ( F ( X ) ≤ y ) = P ( X ≤ F − 1 ( y ) ) = F ( F − 1 ( y ) ) = y P(F(X) ≤ y) = P(X ≤ F⁻¹(y)) = F(F⁻¹(y)) = y P(F(X)≤y)=P(X≤F−1(y))=F(F−1(y))=y,即 G ( y ) = y G(y)=y G(y)=y。
- 验证均匀分布定义
Y的分布函数G(y)完全符合[0,1]上均匀分布的分布函数形式,故Y~U(0,1)。
F(x,y)与f(x,y)
已知 F ( x , y ) F(x,y) F(x,y),如何求 f ( x , y ) f(x,y) f(x,y)?
联合概率密度
f
(
x
,
y
)
f(x,y)
f(x,y) 等于联合分布函数
F
(
x
,
y
)
F(x,y)
F(x,y) 对
x
x
x 和
y
y
y 的二阶混合偏导数,也等于对
y
y
y 和
x
x
x 的二阶混合偏导数,即:
f
(
x
,
y
)
=
∂
2
F
(
x
,
y
)
∂
x
∂
y
=
∂
2
F
(
x
,
y
)
∂
y
∂
x
f(x,y) = \frac{\partial^2 F(x,y)}{\partial x \partial y} = \frac{\partial^2 F(x,y)}{\partial y \partial x}
f(x,y)=∂x∂y∂2F(x,y)=∂y∂x∂2F(x,y)
已知 F ( x , y ) F(x,y) F(x,y),如何求 F Y ( y ) F_Y(y) FY(y)和 F X ( x ) F_X(x) FX(x)、 f Y ( y ) f_Y(y) fY(y)和 f X ( x ) f_X(x) fX(x)?
F X ( x ) = F ( x , + ∞ ) F_X(x) = F(x, +\infty) FX(x)=F(x,+∞)
F Y ( y ) = F ( + ∞ , y ) F_Y(y) = F(+\infty, y) FY(y)=F(+∞,y)
f X ( x ) = F X ′ ( x ) f_X(x) = F_X'(x) fX(x)=FX′(x)
f Y ( y ) = F Y ′ ( y ) f_Y(y) = F_Y'(y) fY(y)=FY′(y)
已知 F ( x , y ) F(x,y) F(x,y),如何求 F X ∣ Y ( x ∣ y ) F_{X|Y}(x|y) FX∣Y(x∣y)、 f X ∣ Y ( x ∣ y ) f_{X|Y}(x|y) fX∣Y(x∣y)?
F X ∣ Y ( x ∣ y ) = ∫ − ∞ x f ( x , y ) f Y ( y ) d x F_{X|Y}(x|y) = \int_{-\infty}^{x} \frac{f(x, y)}{f_Y(y)} dx FX∣Y(x∣y)=∫−∞xfY(y)f(x,y)dx
证明过程如下

p ( x ∣ y ) = d F ( x ∣ y ) d x = d d x ∫ − ∞ x p ( u , y ) p Y ( y ) d u = p ( x , y ) p Y ( y ) \begin{align*} p(x|y) &= \frac{dF(x|y)}{dx} \\ &= \frac{d}{dx} \int_{-\infty}^{x} \frac{p(u,y)}{p_Y(y)} du \\ &= \frac{p(x,y)}{p_Y(y)} \end{align*} p(x∣y)=dxdF(x∣y)=dxd∫−∞xpY(y)p(u,y)du=pY(y)p(x,y)
独立和不相关之间的关系
独立一定不相关,但不相关不一定独立,仅在特定分布(如正态分布)下,独立和不相关可以等价。
1. 独立→不相关:必然成立
- 若随机变量X和Y相互独立,意味着它们的取值完全互不影响,联合概率密度等于边缘概率密度的乘积。
- 从协方差定义推导:Cov(X,Y) = E[XY] - E[X]E[Y],独立时E[XY] = E[X]E[Y],故Cov(X,Y)=0。
- 而相关系数ρ = Cov(X,Y)/(√DX·√DY),Cov(X,Y)=0则ρ=0,即X和Y不相关。
2. 不相关≠独立:普遍情况
- 不相关仅表示X和Y线性无关(相关系数ρ=0),但可能存在非线性关系(如二次、三角函数关系)。
- 示例:设X~N(0,1),Y=X²。计算得Cov(X,Y)=0(不相关),但Y完全由X决定,显然不独立。
3. 特殊情况:不相关=独立
- 当X和Y均服从正态分布(包括二维正态分布)时,不相关与独立等价。
- 注意:需满足“联合正态分布”,仅单个变量正态不成立,必须是二维整体服从正态分布。
如何判断两个随机变量是否独立?
1. 求两个随机变量的联合概率密度函数,看它是否可以拆成两个边缘概率密度函数的乘积(看下面这个例子)

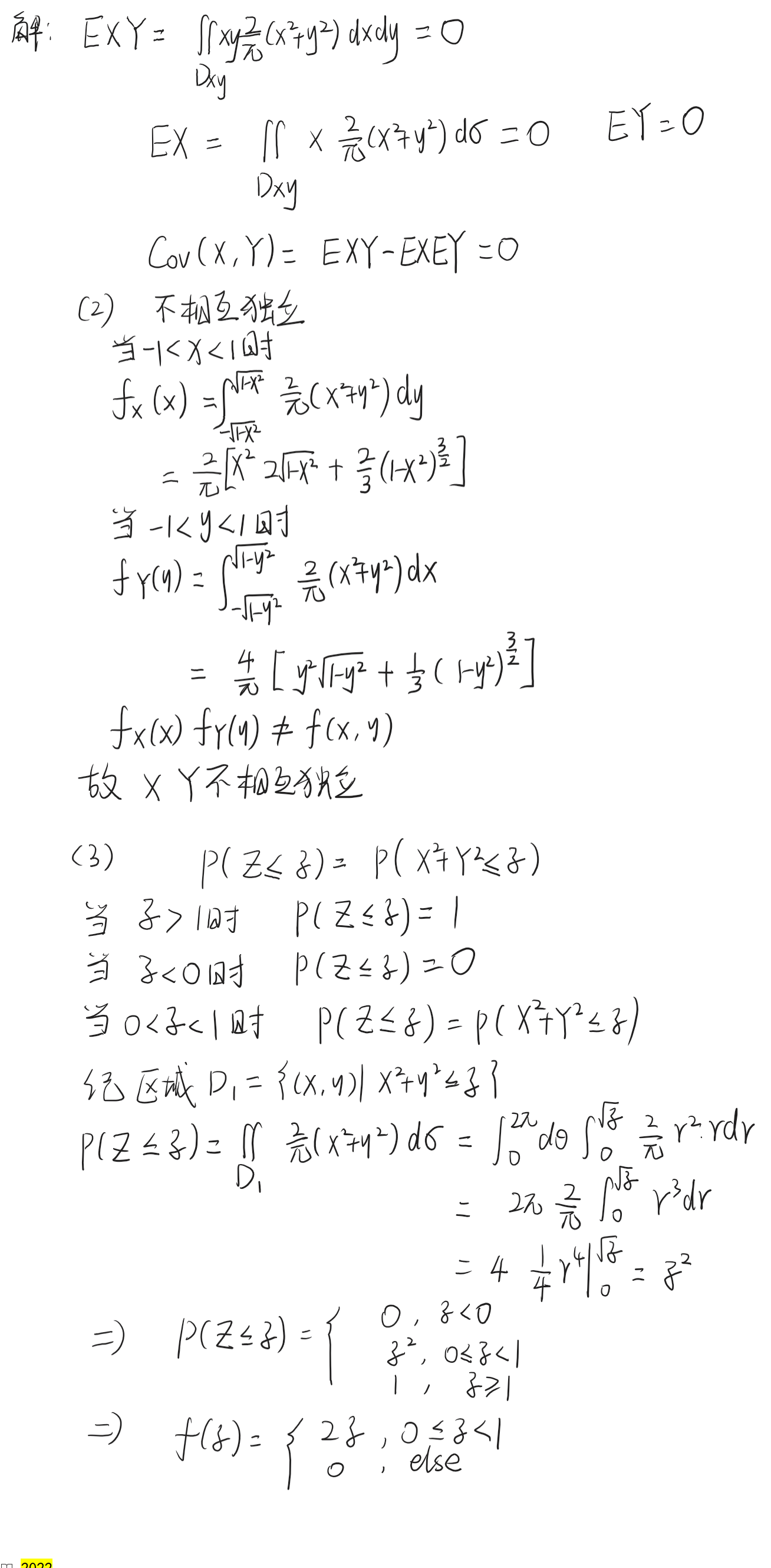
2. 举一个反例说明它不独立(比如下面这个题的第三问)


样本均值 X ˉ \bar{X} Xˉ和样本方差 S 2 S^2 S2是否相互独立?
对于服从一般分布的总体,样本均值 X ˉ \bar{X} Xˉ和样本方差 S 2 S^2 S2通常存在依赖关系(因为 S 2 S^2 S2的计算包含 X ˉ \bar{X} Xˉ),因此不独立。
但是如果总体服从正态分布
X
∼
N
(
μ
,
σ
2
)
X \sim N(\mu, \sigma^2)
X∼N(μ,σ2),则样本均值
X
ˉ
\bar{X}
Xˉ与样本方差
S
2
S^2
S2是相互独立的,且满足:
X
ˉ
∼
N
(
μ
,
σ
2
n
)
,
(
n
−
1
)
S
2
σ
2
∼
χ
2
(
n
−
1
)
\bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right), \quad \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)
Xˉ∼N(μ,nσ2),σ2(n−1)S2∼χ2(n−1)
如果两个随机变量的协方差为0,能否说明这俩随机变量相互独立?
一般是不行的。但是对于两个服从正态分布的随机变量来说,是可以的
亚当夏娃公式

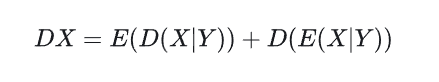
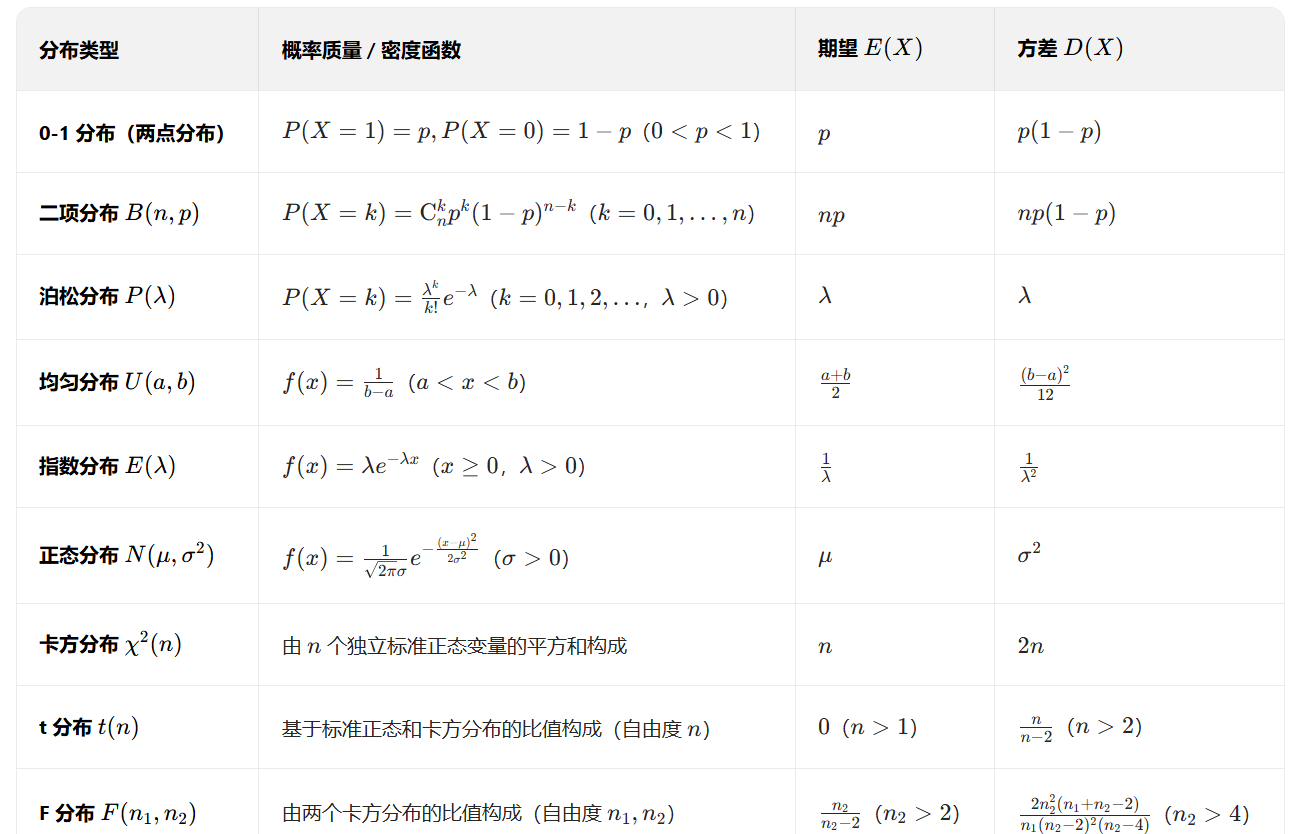
常见分布及其期望方差


如果随机变量X和Y相互独立,分别都服从泊松分布,请问X+Y是否服从泊松分布?

已知 X i ∼ N ( μ , σ 2 ) X_i \sim N(\mu,\sigma^2) Xi∼N(μ,σ2),为什么 ∑ i = 1 n ( X i − X ˉ ) 2 σ 2 ∼ χ 2 ( n − 1 ) \frac{\sum_{i=1}^{n}(X_i-\bar{X})^2}{\sigma^2} \sim \chi^2(n-1) σ2∑i=1n(Xi−Xˉ)2∼χ2(n−1)?

为什么 S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2 S2=n−11∑i=1n(Xi−Xˉ)2,而不是 1 n ∑ i = 1 n ( X i − X ˉ ) 2 \frac{1}{n}\sum_{i=1}^{n}(X_i-\bar{X})^2 n1∑i=1n(Xi−Xˉ)2
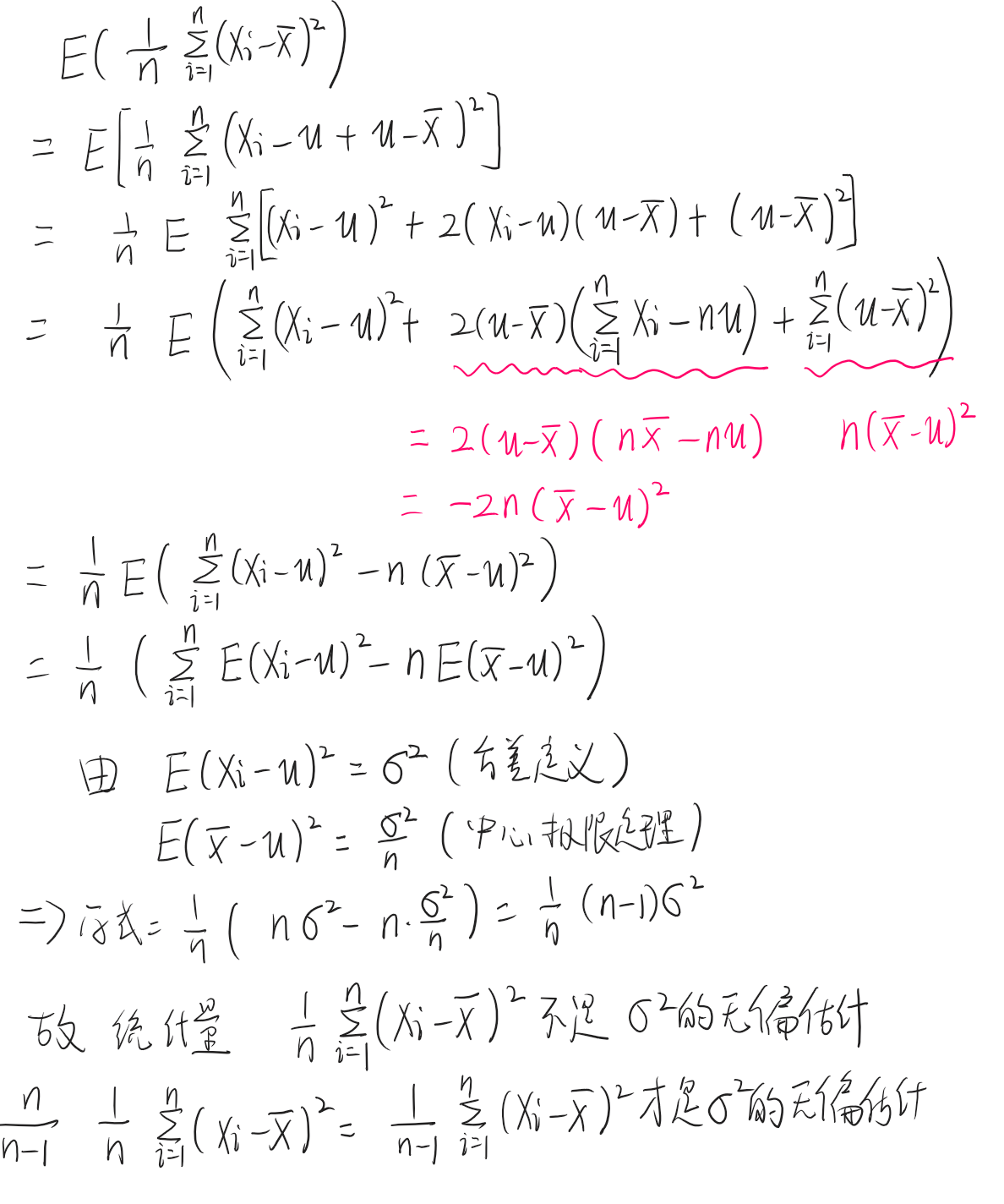
E ( 2 X ) = ? 2 E [ X ] . E(2^X)\; \overset{?}{=}\; 2^{E[X]}. E(2X)=?2E[X].
一般情况下,这个等式不成立!
因为函数 2 x 2^x 2x 是 严格凸函数(二阶导数 ( ln 2 ) 2 2 x > 0 (\ln 2)^2 2^x > 0 (ln2)22x>0)。
根据 Jensen 不等式
E ( 2 X ) ≥ 2 E [ X ] , E(2^X) \ge 2^{E[X]}, E(2X)≥2E[X],
且 只有当 X X X 是常数(退化随机变量)时才会取等号。
也就是说:
-
若 X X X 有随机性,哪怕很小,都会有
E ( 2 X ) > 2 E [ X ] . E(2^X) > 2^{E[X]}. E(2X)>2E[X].
✔ 那正确的关系是什么呢?
E ( 2 X ) ≥ 2 E [ X ] \boxed{ E(2^X) \ge 2^{E[X]} } E(2X)≥2E[X]
并且 只有当 X 为常数时才能取等号。
已知随机变量X和Y都服从标准正态分布,且X和Y相互独立,求 Z = X 2 + Y 2 Z = X^2 + Y^2 Z=X2+Y2 的概率分布
Z = X 2 + Y 2 Z = X^2 + Y^2 Z=X2+Y2 既服从自由度为2的卡方分布,也服从参数为 1 2 \frac{1}{2} 21的指数分布,两种说法是等价的
f ( x , y ) = 1 2 π e − x 2 2 ⋅ 1 2 π e − y 2 2 = 1 2 π e − x 2 + y 2 2 f(x,y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}} = \frac{1}{2\pi} e^{-\frac{x^2+y^2}{2}} f(x,y)=2π1e−2x2⋅2π1e−2y2=2π1e−2x2+y2
F ( Z ) = P { Z ≤ z } = P { X 2 + Y 2 ≤ z } = ∬ D f ( x , y ) d x d y D = { ( x , y ) ∣ x 2 + y 2 ≤ z } = ∫ 0 2 π d θ ∫ 0 z 1 2 π e − r 2 2 ⋅ r d r = ∫ 0 z e − r 2 2 ⋅ d r 2 2 = 1 − e − z 2 \begin{aligned} F(Z) &= P\{Z \leq z\} = P\{X^2+Y^2 \leq z\} \\ &= \iint_D f(x,y) dxdy \quad D=\{(x,y)|x^2+y^2 \leq z\} \\ &= \int_{0}^{2\pi} d\theta \int_{0}^{\sqrt{z}} \frac{1}{2\pi} e^{-\frac{r^2}{2}} \cdot rdr \\ &= \int_{0}^{\sqrt{z}} e^{-\frac{r^2}{2}} \cdot d\frac{r^2}{2} = 1 - e^{-\frac{z}{2}} \end{aligned} F(Z)=P{Z≤z}=P{X2+Y2≤z}=∬Df(x,y)dxdyD={(x,y)∣x2+y2≤z}=∫02πdθ∫0z2π1e−2r2⋅rdr=∫0ze−2r2⋅d2r2=1−e−2z
统计量
这两个统计量(样本均值 X ˉ \bar{X} Xˉ和样本方差 S 2 S^2 S2)不是独立的随机变量,但在正态总体的前提下,它们是相互独立的。
伽马函数
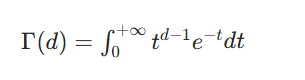
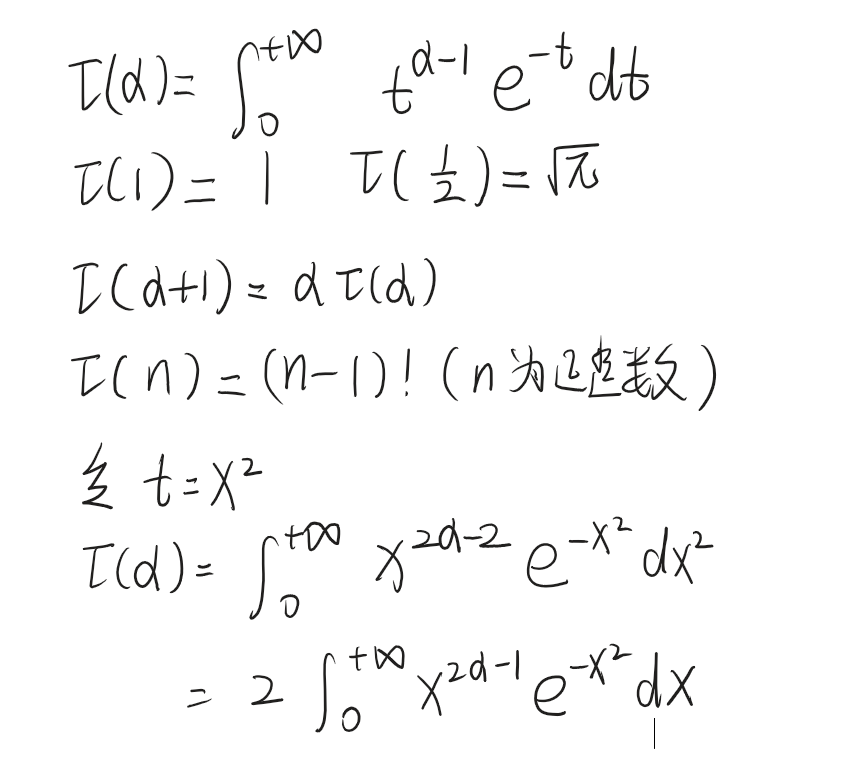
切比雪夫不等式
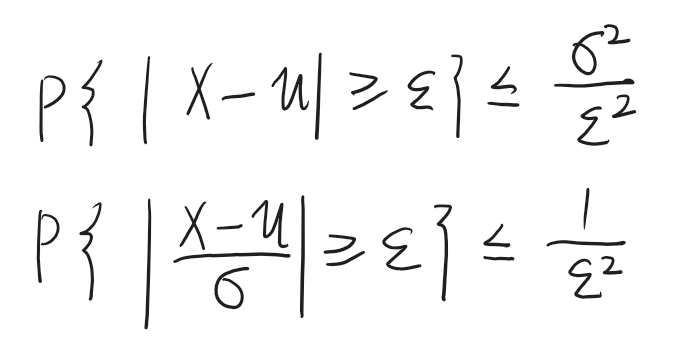
请问上面俩式子是等价的嘛?
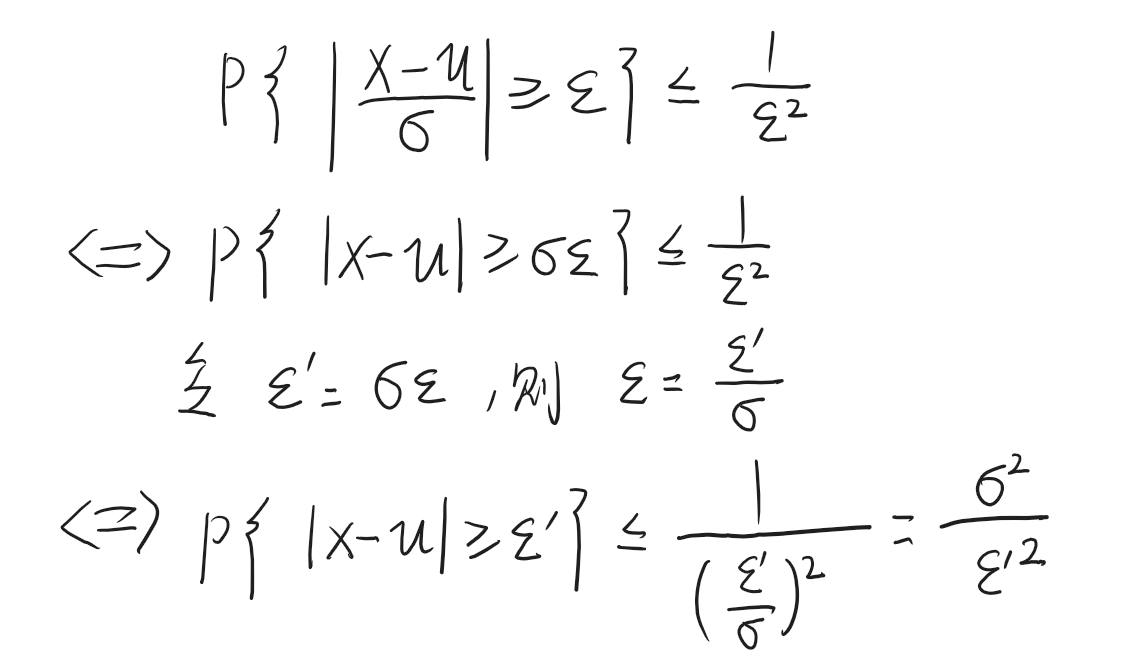
柯西-施瓦茨不等式
什么是柯西施瓦茨不等式?
简单的说,就是向量的内积小于等于两个向量的模之积,常见的形式如下
( ∑ i = 1 n a i b i ) 2 ≤ ( ∑ i = 1 n a i 2 ) ( ∑ i = 1 n b i 2 ) \left( \sum_{i=1}^n a_i b_i \right)^2 \leq \left( \sum_{i=1}^n a_i^2 \right) \left( \sum_{i=1}^n b_i^2 \right) (i=1∑naibi)2≤(i=1∑nai2)(i=1∑nbi2)
还有积分形式的柯西施瓦茨不等式
(
∫
a
b
f
(
x
)
g
(
x
)
d
x
)
2
≤
(
∫
a
b
f
(
x
)
2
d
x
)
(
∫
a
b
g
(
x
)
2
d
x
)
\left( \int_{a}^{b} f(x)g(x)dx \right)^2 \leq \left( \int_{a}^{b} f(x)^2dx \right) \left( \int_{a}^{b} g(x)^2dx \right)
(∫abf(x)g(x)dx)2≤(∫abf(x)2dx)(∫abg(x)2dx)
证明方法也很简单,主要有判别式法和几何法两种。几何法就是我们前面刚刚说的,通过向量内积小于等于两个向量的模之积,这一基本常识直接推出。判别式法的话下面就有
为什么相关系数的绝对值一定小于等于1?(为什么 Cov 2 ( X , Y ) ≤ Cov ( X , X ) Cov ( Y , Y ) \text{Cov}^2(X,Y) ≤ \text{Cov}(X,X)\text{Cov}(Y,Y) Cov2(X,Y)≤Cov(X,X)Cov(Y,Y))
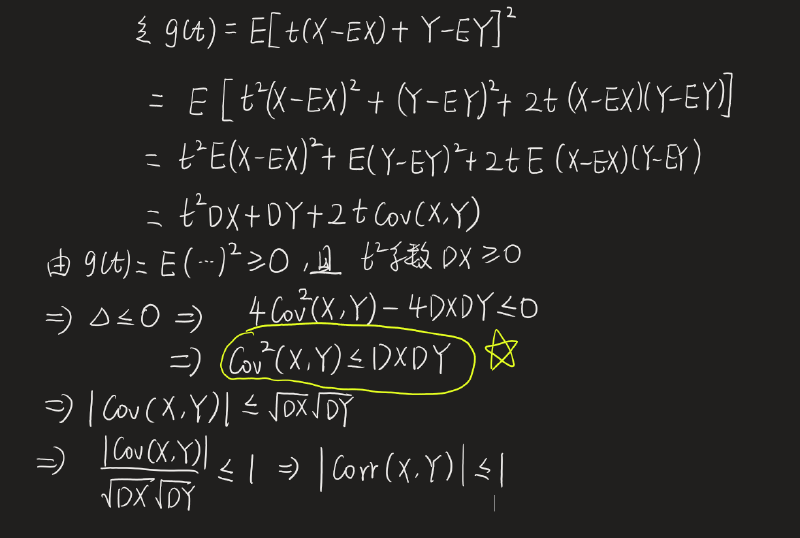
为什么 E 2 ( X Y ) ≤ E ( X 2 ) E ( Y 2 ) E^2(XY) \leq E(X^2)E(Y^2) E2(XY)≤E(X2)E(Y2)?
对任意实数
t
t
t,考虑随机变量
(
t
X
−
Y
)
(tX - Y)
(tX−Y) 的平方(平方数必然非负,所以它的期望也非负):
E
[
(
t
X
−
Y
)
2
]
≥
0
E\left[(tX - Y)^2\right] \geq 0
E[(tX−Y)2]≥0
展开左边:
t
2
E
(
X
2
)
−
2
t
E
(
X
Y
)
+
E
(
Y
2
)
≥
0
t^2 E(X^2) - 2t E(XY) + E(Y^2) \geq 0
t2E(X2)−2tE(XY)+E(Y2)≥0
这是一个关于
t
t
t 的二次函数,且恒非负,因此其判别式必须满足“判别式 ≤ 0”(二次函数恒非负的条件):
Δ
=
[
−
2
E
(
X
Y
)
]
2
−
4
⋅
E
(
X
2
)
⋅
E
(
Y
2
)
≤
0
\Delta = [ -2E(XY) ]^2 - 4 \cdot E(X^2) \cdot E(Y^2) \leq 0
Δ=[−2E(XY)]2−4⋅E(X2)⋅E(Y2)≤0
化简得:
E
2
(
X
Y
)
≤
E
(
X
2
)
E
(
Y
2
)
E^2(XY) \leq E(X^2)E(Y^2)
E2(XY)≤E(X2)E(Y2)
为什么平方的期望大于等于期望的平方?
最直接的原因就是,方差等于平方的期望减去期望的平方,而方差是大于等于0的,所以平方的期望大于等于期望的平方(对任意随机变量 X X X,有 E ( X 2 ) ≥ E 2 ( X ) E(X^2) \geq E^2(X) E(X2)≥E2(X),因为 E ( X 2 ) − E 2 ( X ) = D X ≥ 0 E(X^2) - E^2(X) = DX \geq 0 E(X2)−E2(X)=DX≥0)
为什么 E ( ∣ X ∣ ) ≤ E ( X 2 ) E(|X|) \leq \sqrt{E(X^2)} E(∣X∣)≤E(X2)?
已知“平方的期望 ≥ 期望的平方”
令
Z
=
∣
X
∣
Z = |X|
Z=∣X∣,则:
E
(
∣
X
∣
2
)
≥
E
2
(
∣
X
∣
)
E(|X|^2) \geq E^2(|X|)
E(∣X∣2)≥E2(∣X∣)
而
∣
X
∣
2
=
X
2
|X|^2 = X^2
∣X∣2=X2,所以:
E
(
X
2
)
≥
E
2
(
∣
X
∣
)
E(X^2) \geq E^2(|X|)
E(X2)≥E2(∣X∣)
两边开平方(都是非负数):
E
(
X
2
)
≥
E
(
∣
X
∣
)
\sqrt{E(X^2)} \geq E(|X|)
E(X2)≥E(∣X∣)
Jensen 不等式
前提条件
- 函数 f f f定义在凸集 D D D上;
- 权重 λ 1 , λ 2 , … , λ n ≥ 0 \lambda_1, \lambda_2, \dots, \lambda_n \geq 0 λ1,λ2,…,λn≥0,且满足 ∑ i = 1 n λ i = 1 \sum_{i=1}^n \lambda_i = 1 ∑i=1nλi=1(即“凸组合”的权重)。
凸函数的Jensen 不等式
如果f(x)在D上是凸函数,则对于任意
x
i
∈
D
x_i∈D
xi∈D,都有
f
(
∑
i
=
1
n
λ
i
x
i
)
≤
∑
i
=
1
n
λ
i
f
(
x
i
)
f\left( \sum_{i=1}^n \lambda_i x_i \right) \leq \sum_{i=1}^n \lambda_i f(x_i)
f(i=1∑nλixi)≤i=1∑nλif(xi)
几何意义:凸函数的图像始终“位于割线下方”
如果f(x)在D内是凹函数,则对于任意
x
i
∈
D
x_i∈D
xi∈D,都有
f
(
∑
i
=
1
n
λ
i
x
i
)
≥
∑
i
=
1
n
λ
i
f
(
x
i
)
f\left( \sum_{i=1}^n \lambda_i x_i \right) \geq \sum_{i=1}^n \lambda_i f(x_i)
f(i=1∑nλixi)≥i=1∑nλif(xi)
几何意义:凹函数图像始终位于“位于割线上方”;
大数定律
当样本量n 趋近于无穷时,样本均值依概率收敛于总体的期望

中心极限定理
现有n个独立同分布的随机变量X1 ~ Xn,无论 Xi 服从什么分布,只要我们对样本均值进行标准化,当样本容量n趋近于无穷时,得到的随机变量一定服从标准正态分布

常见统计量及其分布
正态分布
对于标准正态分布 X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1),关于其偶次幂 X 2 n X^{2n} X2n 的矩与方差都有一般性结论。
✅ 1. 正态分布的偶数阶矩
标准正态的偶数阶矩为:
E ( X 2 n ) = ( 2 n − 1 ) ! ! E(X^{2n}) = (2n - 1)!! E(X2n)=(2n−1)!!
其中 ( 2 n − 1 ) ! ! (2n-1)!! (2n−1)!! 是双阶乘。例如:
- E ( X 2 ) = 1 E(X^2) = 1 E(X2)=1
- E ( X 4 ) = 3 E(X^4) = 3 E(X4)=3
- E ( X 6 ) = 15 E(X^6) = 15 E(X6)=15
- E ( X 8 ) = 105 E(X^8) = 105 E(X8)=105
而奇数阶矩均为 0。
✅ 2. 正态分布的偶次幂方差
我们要的是:
D ( X 2 n ) = E ( X 4 n ) − ( E ( X 2 n ) ) 2 D(X^{2n}) = E(X^{4n}) - (E(X^{2n}))^2 D(X2n)=E(X4n)−(E(X2n))2
使用偶数阶矩公式:
E ( X 4 n ) = ( 4 n − 1 ) ! ! E(X^{4n}) = (4n - 1)!! E(X4n)=(4n−1)!!
因此得到标准正态 X 2 n X^{2n} X2n 的方差的一般表达式:
D ( X 2 n ) = ( 4 n − 1 ) ! ! − ( ( 2 n − 1 ) ! ! ) 2 \boxed{ D(X^{2n}) = (4n - 1)!! - \big((2n - 1)!!\big)^2 } D(X2n)=(4n−1)!!−((2n−1)!!)2
总结
对于 X ∼ N ( 0 , 1 ) X\sim N(0,1) X∼N(0,1),有一般公式:
偶数阶矩:
E ( X 2 n ) = ( 2 n − 1 ) ! ! E(X^{2n}) = (2n-1)!! E(X2n)=(2n−1)!!
偶次幂方差:
D ( X 2 n ) = ( 4 n − 1 ) ! ! − ( ( 2 n − 1 ) ! ! ) 2 \boxed{ D(X^{2n}) = (4n - 1)!! - \big((2n - 1)!!\big)^2 } D(X2n)=(4n−1)!!−((2n−1)!!)2
二维联合正态分布
若二维随机变量
(
X
,
Y
)
(X, Y)
(X,Y) 的联合概率密度函数为:
f
(
x
,
y
)
=
1
2
π
σ
1
σ
2
1
−
ρ
2
exp
{
−
1
2
(
1
−
ρ
2
)
[
(
x
−
μ
1
)
2
σ
1
2
−
2
ρ
(
x
−
μ
1
)
(
y
−
μ
2
)
σ
1
σ
2
+
(
y
−
μ
2
)
2
σ
2
2
]
}
f(x,y) = \frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}} \exp\left\{ -\frac{1}{2(1-\rho^2)}\left[ \frac{(x-\mu_1)^2}{\sigma_1^2} - 2\rho\frac{(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2} + \frac{(y-\mu_2)^2}{\sigma_2^2} \right] \right\}
f(x,y)=2πσ1σ21−ρ21exp{−2(1−ρ2)1[σ12(x−μ1)2−2ρσ1σ2(x−μ1)(y−μ2)+σ22(y−μ2)2]}
其中
x
,
y
∈
(
−
∞
,
+
∞
)
x, y \in (-\infty, +\infty)
x,y∈(−∞,+∞),则称
(
X
,
Y
)
(X, Y)
(X,Y) 服从二维联合正态分布,记为
(
X
,
Y
)
∼
N
(
μ
1
,
μ
2
;
σ
1
2
,
σ
2
2
;
ρ
)
(X, Y) \sim N(\mu_1, \mu_2; \sigma_1^2, \sigma_2^2; \rho)
(X,Y)∼N(μ1,μ2;σ12,σ22;ρ)。
关键参数及含义
- μ 1 = E ( X ) \mu_1 = E(X) μ1=E(X)、 μ 2 = E ( Y ) \mu_2 = E(Y) μ2=E(Y):分别是随机变量 X X X、 Y Y Y 的边缘均值,决定联合分布的中心位置。
- σ 1 2 = D ( X ) \sigma_1^2 = D(X) σ12=D(X)、 σ 2 2 = D ( Y ) \sigma_2^2 = D(Y) σ22=D(Y):分别是 X X X、 Y Y Y 的边缘方差( σ 1 > 0 \sigma_1 > 0 σ1>0、 σ 2 > 0 \sigma_2 > 0 σ2>0),描述单个变量的离散程度。
-
ρ
=
Cov
(
X
,
Y
)
/
(
σ
1
σ
2
)
\rho = \text{Cov}(X,Y)/(\sigma_1\sigma_2)
ρ=Cov(X,Y)/(σ1σ2):
X
X
X 与
Y
Y
Y 的相关系数,取值范围为
[
−
1
,
1
]
[-1, 1]
[−1,1],描述两者的线性相关程度:
- ρ = 0 \rho = 0 ρ=0: X X X 与 Y Y Y 线性无关;
- ρ > 0 \rho > 0 ρ>0:正相关, ρ \rho ρ 越接近1,正相关性越强;
- ρ < 0 \rho < 0 ρ<0:负相关, ρ \rho ρ 越接近-1,负相关性越强。
核心性质
- 边缘分布仍为正态分布:若 ( X , Y ) (X, Y) (X,Y) 服从二维联合正态分布,则 X ∼ N ( μ 1 , σ 1 2 ) X \sim N(\mu_1, \sigma_1^2) X∼N(μ1,σ12), Y ∼ N ( μ 2 , σ 2 2 ) Y \sim N(\mu_2, \sigma_2^2) Y∼N(μ2,σ22)。
- 线性无关等价于独立:对二维联合正态分布, X X X 与 Y Y Y 线性无关( ρ = 0 \rho = 0 ρ=0)的充要条件是 X X X 与 Y Y Y 相互独立。
- 线性组合仍为正态分布:任意线性组合
a
X
+
b
Y
+
c
aX + bY + c
aX+bY+c(
a
,
b
a, b
a,b 不同时为0)仍服从一维正态分布,参数为:
- 均值: a μ 1 + b μ 2 + c a\mu_1 + b\mu_2 + c aμ1+bμ2+c
- 方差: a 2 σ 1 2 + b 2 σ 2 2 + 2 a b ρ σ 1 σ 2 a^2\sigma_1^2 + b^2\sigma_2^2 + 2ab\rho\sigma_1\sigma_2 a2σ12+b2σ22+2abρσ1σ2
- 条件分布仍为正态分布:给定 Y = y Y = y Y=y 时, X X X 的条件分布为 N ( μ 1 + ρ σ 1 σ 2 ( y − μ 2 ) , σ 1 2 ( 1 − ρ 2 ) ) N\left( \mu_1 + \rho\frac{\sigma_1}{\sigma_2}(y - \mu_2), \sigma_1^2(1 - \rho^2) \right) N(μ1+ρσ2σ1(y−μ2),σ12(1−ρ2));反之亦然。
特殊情况:标准二维联合正态分布
当
μ
1
=
μ
2
=
0
\mu_1 = \mu_2 = 0
μ1=μ2=0、
σ
1
2
=
σ
2
2
=
1
\sigma_1^2 = \sigma_2^2 = 1
σ12=σ22=1 时,称为标准二维联合正态分布,密度函数简化为:
f
(
x
,
y
)
=
1
2
π
1
−
ρ
2
exp
{
−
x
2
−
2
ρ
x
y
+
y
2
2
(
1
−
ρ
2
)
}
f(x,y) = \frac{1}{2\pi\sqrt{1-\rho^2}} \exp\left\{ -\frac{x^2 - 2\rho xy + y^2}{2(1-\rho^2)} \right\}
f(x,y)=2π1−ρ21exp{−2(1−ρ2)x2−2ρxy+y2}
如果X和Y均服从正态分布,但X和Y不相互独立,请问X+Y还服从正态分布吗?
如果X和Y服从二维联合正态分布,即使X与Y不相互独立,他们的和依然服从正态分布
已知X和Y分别服从正态分布,那么 任意线性组合 a X + b Y + c aX + bY + c aX+bY+c( a , b a, b a,b 不同时为0)仍服从一维正态分布 是 X和Y服从二维联合正态分布 的等价条件
看下面的例子:已知二维随机变量 ( X , Y ) ∼ N ( 0 , 2 ; σ 2 , σ 2 ; 1 2 ) (X,Y) \sim N\left(0,2;\sigma^2,\sigma^2;\frac{1}{2}\right) (X,Y)∼N(0,2;σ2,σ2;21),求 Z = X + Y Z=X+ Y Z=X+Y的分布

卡方分布
若 X ∼ χ 2 ( n ) X \sim \chi^2(n) X∼χ2(n),则 E X = n EX = n EX=n, D X = 2 n DX = 2n DX=2n。
T分布
T分布的定义
设随机变量 X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1), Y ∼ χ 2 ( n ) Y \sim \chi^2(n) Y∼χ2(n), X X X与 Y Y Y相互独立,则随机变量 t = X Y / n t = \frac{X}{\sqrt{Y / n}} t=Y/nX服从自由度为 n n n的 t t t分布,记为 t ∼ t ( n ) t \sim t(n) t∼t(n)。
上 α \alpha α分位数定义
对给定的 α ( 0 < α < 1 ) \alpha(0 < \alpha < 1) α(0<α<1),称满足 P { t > t α ( n ) } = α P\{t > t_{\alpha}(n)\} = \alpha P{t>tα(n)}=α的 t α ( n ) t_{\alpha}(n) tα(n)为 t ( n ) t(n) t(n)分布的上 α \alpha α分位数
T分布的性质
-
t t t分布概率密度 f ( x ) f(x) f(x)的图形关于 x = 0 x = 0 x=0对称,因此 E t = 0 ( n ≥ 2 ) Et = 0(n \geq 2) Et=0(n≥2)
-
当 n = 1 n = 1 n=1时,即若 X ∼ N ( 0 , 1 ) X \sim N(0,1) X∼N(0,1), Y ∼ χ 2 ( 1 ) Y \sim \chi^2(1) Y∼χ2(1),则 X Y ∼ f ( x ) = 1 π ( 1 + x 2 ) \frac{X}{\sqrt{Y}} \sim f(x) = \frac{1}{\pi(1 + x^2)} YX∼f(x)=π(1+x2)1
F分布
F分布概念
设随机变量
X
∼
χ
2
(
n
1
)
X \sim \chi^2(n_1)
X∼χ2(n1),
Y
∼
χ
2
(
n
2
)
Y \sim \chi^2(n_2)
Y∼χ2(n2),且
X
X
X与
Y
Y
Y相互独立,则
F
=
X
/
n
1
Y
/
n
2
F = \frac{X / n_1}{Y / n_2}
F=Y/n2X/n1服从自由度为
(
n
1
,
n
2
)
(n_1, n_2)
(n1,n2)的F分布,记为
F
∼
F
(
n
1
,
n
2
)
F \sim F(n_1, n_2)
F∼F(n1,n2),其中
n
1
n_1
n1称为第一自由度,
n
2
n_2
n2称为第二自由度
F分布的图像
F分布的概率密度
f
(
x
)
f(x)
f(x)的图形如下图所示
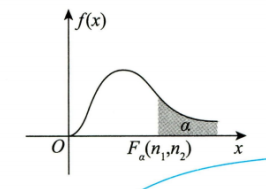
F分布的性质
①若 F ∼ F ( n 1 , n 2 ) F \sim F(n_1, n_2) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \frac{1}{F} \sim F(n_2, n_1) F1∼F(n2,n1)
② F 1 − α ( n 1 , n 2 ) = 1 F α ( n 2 , n 1 ) F_{1-\alpha}(n_1, n_2) = \frac{1}{F_{\alpha}(n_2, n_1)} F1−α(n1,n2)=Fα(n2,n1)1。常用来求 F F F分布表中未列出的上 α \alpha α分位数,显然,有些特殊值可直接得出,如 1 − α = α 1-\alpha = \alpha 1−α=α, n 1 = n 2 = n n_1 = n_2 = n n1=n2=n时,有 F 0.5 ( n , n ) = 1 F 0.5 ( n , n ) F_{0.5}(n, n) = \frac{1}{F_{0.5}(n, n)} F0.5(n,n)=F0.5(n,n)1,且 F 0.5 ( n , n ) > 0 F_{0.5}(n, n) > 0 F0.5(n,n)>0,故 F 0.5 ( n , n ) = 1 F_{0.5}(n, n) = 1 F0.5(n,n)=1
证明:设
F
∼
F
(
n
2
,
n
1
)
F \sim F(n_2, n_1)
F∼F(n2,n1),则
P
{
F
>
F
α
(
n
2
,
n
1
)
}
=
α
P\{F > F_{\alpha}(n_2, n_1)\} = \alpha
P{F>Fα(n2,n1)}=α,
P
{
F
≤
F
α
(
n
2
,
n
1
)
}
=
1
−
α
P\{F \leq F_{\alpha}(n_2, n_1)\} = 1-\alpha
P{F≤Fα(n2,n1)}=1−α,
P
{
1
F
≥
1
F
α
(
n
2
,
n
1
)
}
=
1
−
α
P\left\{\frac{1}{F} \geq \frac{1}{F_{\alpha}(n_2, n_1)}\right\} = 1-\alpha
P{F1≥Fα(n2,n1)1}=1−α。
因为
1
F
∼
F
(
n
1
,
n
2
)
\frac{1}{F} \sim F(n_1, n_2)
F1∼F(n1,n2),结合上
α
\alpha
α分位数的定义,可知
1
F
α
(
n
2
,
n
1
)
=
F
1
−
α
(
n
1
,
n
2
)
\frac{1}{F_{\alpha}(n_2, n_1)} = F_{1-\alpha}(n_1, n_2)
Fα(n2,n1)1=F1−α(n1,n2)
③若 t ∼ t ( n ) t \sim t(n) t∼t(n),则 t 2 ∼ F ( 1 , n ) t^2 \sim F(1, n) t2∼F(1,n)。
正态分布相关常用统计量
设 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn是取自正态总体 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)的一个样本, X ˉ \bar{X} Xˉ, S 2 S^2 S2分别是样本均值和样本方差,则
① X ˉ ∼ N ( μ , σ 2 n ) \bar{X} \sim N\left( \mu,\frac{\sigma^2}{n} \right) Xˉ∼N(μ,nσ2),即 X ˉ − μ σ n = n ( X ˉ − μ ) σ ∼ N ( 0 , 1 ) \frac{\frac{\bar{X}-\mu}{\sigma}}{\sqrt{n}} = \frac{\sqrt{n}(\bar{X}-\mu)}{\sigma} \sim N(0,1) nσXˉ−μ=σn(Xˉ−μ)∼N(0,1);
② 1 σ 2 ∑ i = 1 n ( X i − μ ) 2 ∼ χ 2 ( n ) \frac{1}{\sigma^2}\sum_{i=1}^{n}(X_i - \mu)^2 \sim \chi^2(n) σ21∑i=1n(Xi−μ)2∼χ2(n);
③ ( n − 1 ) S 2 σ 2 = ∑ i = 1 n ( X i − X ˉ σ ) 2 ∼ χ 2 ( n − 1 ) \frac{(n-1)S^2}{\sigma^2} = \sum_{i=1}^{n}\left( \frac{X_i - \bar{X}}{\sigma} \right)^2 \sim \chi^2(n-1) σ2(n−1)S2=∑i=1n(σXi−Xˉ)2∼χ2(n−1)( μ \mu μ未知,在“②”中用 X ˉ \bar{X} Xˉ替代 μ \mu μ);
④ X ˉ \bar{X} Xˉ与 S 2 S^2 S2相互独立, n ( X ˉ − μ ) S ∼ t ( n − 1 ) \frac{\sqrt{n}(\bar{X}-\mu)}{S} \sim t(n-1) Sn(Xˉ−μ)∼t(n−1)( σ \sigma σ未知,在“①”中用 S S S替代 σ \sigma σ).进一步有 n ( X ˉ − μ ) 2 S 2 ∼ F ( 1 , n − 1 ) \frac{n(\bar{X}-\mu)^2}{S^2} \sim F(1,n-1) S2n(Xˉ−μ)2∼F(1,n−1)
(若 t ∼ t ( n − 1 ) t \sim t(n-1) t∼t(n−1),则 t 2 ∼ F ( 1 , n − 1 ) t^2 \sim F(1,n-1) t2∼F(1,n−1))
区间估计
设 X ∼ N ( μ , σ 2 ) X \sim N(\mu,\sigma^{2}) X∼N(μ,σ2),从总体 X X X中抽取样本 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn,样本均值为 X ˉ \bar{X} Xˉ,样本方差为 S 2 S^2 S2。
① σ 2 \sigma^2 σ2已知, μ \mu μ的置信水平是 1 − α 1-\alpha 1−α的置信区间为
( X ˉ − σ n z α 2 , X ˉ + σ n z α 2 ) \left( \bar{X} - \frac{\sigma}{\sqrt{n}} z_{\frac{\alpha}{2}}, \bar{X} + \frac{\sigma}{\sqrt{n}} z_{\frac{\alpha}{2}} \right) (Xˉ−nσz2α,Xˉ+nσz2α)
记为 I 1 → P { μ ∈ I 1 } = 1 − α I_1 \to P\{\mu \in I_1\} = 1-\alpha I1→P{μ∈I1}=1−α
② σ 2 \sigma^2 σ2未知, μ \mu μ的置信水平是 1 − α 1-\alpha 1−α的置信区间为
( X ˉ − S n t α 2 ( n − 1 ) , X ˉ + S n t α 2 ( n − 1 ) ) \left( \bar{X} - \frac{S}{\sqrt{n}} t_{\frac{\alpha}{2}}(n-1), \bar{X} + \frac{S}{\sqrt{n}} t_{\frac{\alpha}{2}}(n-1) \right) (Xˉ−nSt2α(n−1),Xˉ+nSt2α(n−1))
记为 I 2 → P { μ ∈ I 2 } = 1 − α I_2 \to P\{\mu \in I_2\} = 1-\alpha I2→P{μ∈I2}=1−α
③ μ \mu μ已知, σ 2 \sigma^2 σ2的置信水平是 1 − α 1-\alpha 1−α的置信区间为
( ∑ i = 1 n ( X i − μ ) 2 χ α 2 2 ( n ) , ∑ i = 1 n ( X i − μ ) 2 χ 1 − α 2 2 ( n ) ) \left( \frac{\sum_{i=1}^{n}(X_i - \mu)^2}{\chi_{\frac{\alpha}{2}}^2(n)}, \frac{\sum_{i=1}^{n}(X_i - \mu)^2}{\chi_{1-\frac{\alpha}{2}}^2(n)} \right) (χ2α2(n)∑i=1n(Xi−μ)2,χ1−2α2(n)∑i=1n(Xi−μ)2)
记为 I 3 → P { σ 2 ∈ I 3 } = 1 − α I_3 \to P\{\sigma^2 \in I_3\} = 1-\alpha I3→P{σ2∈I3}=1−α
④ μ \mu μ未知, σ 2 \sigma^2 σ2的置信水平是 1 − α 1-\alpha 1−α的置信区间为
( ( n − 1 ) S 2 χ α 2 2 ( n − 1 ) , ( n − 1 ) S 2 χ 1 − α 2 2 ( n − 1 ) ) \left( \frac{(n-1)S^2}{\chi_{\frac{\alpha}{2}}^2(n-1)}, \frac{(n-1)S^2}{\chi_{1-\frac{\alpha}{2}}^2(n-1)} \right) (χ2α2(n−1)(n−1)S2,χ1−2α2(n−1)(n−1)S2)
记为 I 4 → P { σ 2 ∈ I 4 } = 1 − α I_4 \to P\{\sigma^2 \in I_4\} = 1-\alpha I4→P{σ2∈I4}=1−α
如何求假设检验过程中的拒绝域

拒绝域、显著性水平、置信水平之间的关系
简单理解的话,显著性水平α就是落在拒绝域中的概率,置信水平等于1-显著性水平α,
显著性水平的定义:显著性水平(记为α)是假设检验中,预先设定的“犯第一类错误(弃真错误)的最大允许概率”,常用取值为0.05(5%)、0.01(1%)或0.1(10%)
显著性水平越高(α越小),说明犯第一类错误的概率越小,也就是假设是真的,但你把它拒绝了的概率越小,因此拒绝域也就越小
举个例子:

上面这道题中他说在检验水平α=0.05的情况下拒绝H0,其中α=0.05就意味着犯第一类错误的概率是5%,准确率是95%。此时拒绝H0,说明95%的准确率太低了,要想接受H0,需要更高的准确率
薄弱点实时统计
- 具体行列式的计算(2018年第13题)
- 对立事件相关问题(2017年第7题)





















 37
37

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








