叉积

叉积的计算是线段方法的核心。考虑如图33-1(a)所示的向量p1和p2。我们可以把叉积解释为由点(0,0)，p1，p2 和 p1+p2=(x1+x2,y1+y2)所构成的平行四边形的有向面积。另一种与之等价但更有效的叉积定义方式是将之看做矩阵行列式:

p1×p2=det[x1y1x2y2]=x1y2−x2y1=−p2×p1

若p1×p2值为正,则相对于原点(0,0)来说，p1位于p2的顺时针方向；若p1×p2值为负，则p1位于p2的逆时针方向。图(b)展示了向量p的顺时针和逆时针区域。叉积为0时出现边界情况；在这种情况下，两个向量是共线的，指向相同方向或者相反方向。

　　为了确定相对于公共端点p0，有向线段p0p1−→−是在顺时针还是逆时针方向更接近p0p2−→−，我们将p0作为原点从而使问题简化。用p1-p0来表示向量p′1=(x′1,y′1)，其中x′1=x1−x0，y′1=y1−y0，类似的，可以定义p2-p0。然后，计算叉积

(p1−p0)×(p2−p0)=(x1−x0)(y2−y0)−(x2−x0)(y1−y0)

下面是叉积的用途：

1.叉积判断线段拐向

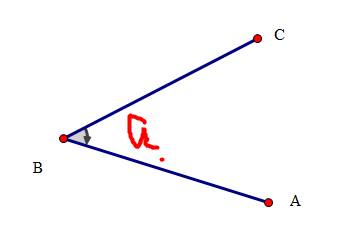
如上图，可以通过计算向量的叉积来判断拐向，即判断（C-B）×（A-B）的符号。
#若（C-B）×（A-B）> 0 ，则CB在B点顺时针得到AB
#若（C-B）×（A-B）< 0 ，则CB在B点逆时针得到AB
#若（C-B）×（A-B）= 0 ，则A，B，C三点共线。

如图，我们给三个点A,B,C,判断沿着AB到BC，在B点是向右拐还是向左拐。并求出拐的 角度。这个先直接用叉积判断拐向，然后再余弦定理计算角度即可，
用180减去这个角度便是拐的角度。

2.叉积还有一个重要的用处，就是用来求面积。

叉积用来求面积，求出的是有向面积，也就是说带正负号，
不过再取一下绝对值就是真正的面积大小了。
比如求三角形ABC的面积，先计算出叉积cross(A,B,C)，
那么面积就是fabs（cross(A,B,C)）/ 2.0
为什么呢？
我们看一下叉积的定义就知道了，a与b的叉积模为：
|a×b|=|a| |b| sin(a,b)他的几何意义就是以a和b为邻边的平行四边形的面积。

3判断点p是否在三角形内。
若在三角形内，则必有S.abc=S.abp+S.acp+S.bcp;若在三角形外，式子就不成立。

4.叉积能判断两直线是否相交。

对于给出的两条线段A1A2，B1B2，判断他们是否相交需要分两步
（1）快速排斥实验
设以线段A1A2和线段B1B2为对角线的矩形为M,N;
若M,N 不相交，则两个线段显然不相交；
判断矩形相交，只需判断某一矩形是否有顶点在另一个矩形内即可。
所以：只有当满足第一个条件时，两个线段才可能相交。
（2）跨立实验
如果两线段相交，则两线段必然相互跨立对方.若A1A2跨立B1B2，则矢量( A1 - B1 ) 和(A2-B1)位于矢量(B2-B1)的两侧，
即：（(A1-B1) × (B2-B1) ）·（ (A2-B1) × (B2-B1)）<0。
上式可以改写成：（(A1-B1) × (B2-B1)） · （(B2-B1) × (A2-B1)）>0。
当(A1-B1) × (B2-B1)=0时，说明A1B1和B2B1共线，但前面已经通过了快速排斥实验，所以A1一定在B1B2上，所以判断线段A1A2是否跨立B1B2的依据就是：
（(A1-B1) × (B2-B1)） · （(B2-B1) × (A2-B1)）>=0。
同理，判断线段B1B2是否跨立A1A2的依据是：（(B1-A1) × (A2-A1)） · （(A2-A1) × (B2-A1)）>=0。