Deranged Exams

最新推荐文章于 2019-07-10 23:21:14 发布

原创最新推荐文章于 2019-07-10 23:21:14 发布 · 210 阅读

0 ·

CC 4.0 BY-SA版权

组合数学专栏收录该内容

1 篇文章

订阅专栏

探讨了在数据结构和算法考试中，学生随机匹配术语与定义的问题，使用容斥原理计算至少前K次匹配错误的情况数。通过分析对立事件，转化为求最多前K次匹配正确的情况，再利用总可能性减去这些情况得到最终答案。

Deranged Exams
The first question on the Data Structures and Algorithms final exam has a list of N terms and a second list of N definitions. Students are to match each term with the correct definition.
Unfortunately, Joe, who wrote a Visual BASIC program in high school and assumed he knew all
there was to know about Computer Science, did not bother to come to class or read the textbook. Hehas to guess randomly what the matches are. Let S(N, k) be the number of ways Joe can answer the question and get at least the first k matches wrong.
For this problem, you will write a program to compute S(N, k).
Input
The first line of input contains a single integer P, (1 ≤ P ≤ 1000), which is the number of data sets
that follow. Each data set should be processed identically and independently.
Each data set consists of a single line of input containing three space separated decimal integers.
The first integer is the data set number. The second integer is the number, N (1 ≤ N ≤ 17), of terms
to be matched in the question. The third integer is the number, k (0 ≤ k ≤ N), of initial matches to
be incorrect.
Output
For each data set there is a single line of output. It contains the data set number followed by a single
space which is then followed by the value of S(N, k).
Sample Input
4
1 4 1
2 7 3
3 10 5
4 17 17
Sample Output
1 18
2 3216
3 2170680
4 130850092279664

题意

有n个术语和n个定义，学生们需要使得术语与定义一一匹配。小明写了一个VB程序，让计算机来帮它完成这项任务。机器是随机匹配的。问至少前K次匹配是错误的情况有多少种？

分析

前K次匹配不好求，转换成求对立事件的个数，即求最多前K次匹配正确，再利用 |Ω - 最多前K次正确| 求得前K次匹配错误的情况数。
至少的对立是至多，前K次匹配错误的对立是前K次匹配不全错误。
最多前K次匹配正确，分为前K次有i次匹配正确( 1 $≤\leq$ i $≤\leq$ k) , 依次求出每种情况，在累加。
求前K次有1次匹配正确的时候,发现保证有一个对的情况下 ( $C_k^1$ $A_{n-1}^{n-1}$ ),这会多算有i个对的情况(1 $≤\leq$ i $≤\leq$ k)。怎么办？减去多算的，经过演算，发现满足容斥原理。

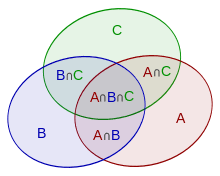
A：匹配第一个
B：匹配第二个
C：匹配第三个

代码

#include <iostream>
using namespace std;
const int N = 110;
typedef long long int LL ;

LL fac[N];
void makeFac(){
    fac[0] = 1;
    for(LL i=1;i<=17;i++)
        fac[i] = fac[i-1]*i;
}

LL C(LL n,LL k){
    return n>=k ? fac[n]/(fac[k]*fac[n-k]) : 0;
}

int main()
{
    makeFac();
    int T;
    cin>>T;
    while(T--) {
        LL i,z,n,k,sum=0;
        cin >> z >> n >> k;
        for(i=1;i<=k;i++)
            i&1 ? sum+=C(k,i)*fac[n-i] : sum-=C(k,i)*fac[n-i];
        cout << z << " " << fac[n]-sum << endl;
    }
    return 0;
}