矩阵基础

定义

由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

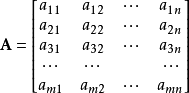
这m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵  。

基本运算

矩阵运算在科学计算中非常重要 ，而矩阵的基本运算包括矩阵的加法，减法，数乘，转置，共轭和共轭转置   。

加法

矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：

应该注意的是只有同型矩阵之间才可以进行加法 [11]  。

减法

数乘

矩阵的数乘满足以下运算律：

矩阵的加减法和矩阵的数乘合称矩阵的线性运算 [8]  。

转置

把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵 [9]  ，这一过程称为矩阵的转置

矩阵的转置满足以下运算律：

共轭

矩阵的共轭定义为:

.一个2×2复数矩阵的共轭如下所示 [12]  ：

则

共轭转置

　　矩阵的共轭转置定义为：

，也可以写为：

[13]  。一个2×2复数矩阵的共轭如下所示：

则

乘法

矩阵乘法

两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，它们的乘积C是一个m×p矩阵

，它的一个元素：

并将此乘积记为:

[9]  .

例如：

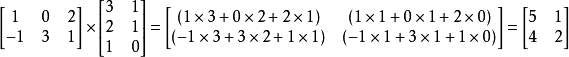
矩阵的乘法满足以下运算律：

结合律：

左分配律：

右分配律：

矩阵乘法不满足交换律。