洛谷P10582 [蓝桥杯 2024 国 A] 最强策略家

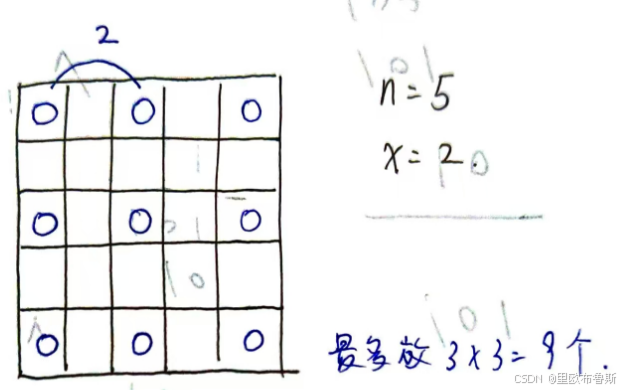
一开始，A可以下两颗子，起初棋盘上很空，棋与棋之间距离大，B只能挡住一颗，随着回合数的增加，B能覆盖的正方形范围越来越大，B能挡住的棋子的数目在某一回合x 后会大于等于2，之后A就不占优势了，没法让棋盘上的棋子的数目增加

在1到x回合，A每次下棋能让棋盘上多一颗子，则第x回合，棋盘上有x个子，第x回合要想不被A遮住两颗子，任意两颗棋子之间的横距离要大于等于x，纵距离也要大于等于x，则第x回合最多放的棋子数目是 ( 向上取整(n/x) )的平方 个，若x大于等于这个数目，则第x回合B覆盖的棋子数目超过了1，(x等于这个数目的时候，第x回合A放的两个子中有一个已经不在了当前局面能放的最密集的子的位置，在第x回合B出手的时候就可以覆盖两个子)，所以二分查找x，使得x严格小于第x回合最多放的棋子数目，找这样的最大的x，则1-x回合能稳定放x个子，之后棋子数量不会超过当前局面了

第x+1回合，A还能再放两个，因此答案+2，答案不能超过棋盘填满时其上的子的数量

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;

#define ll long long

int main()
{
    ios::sync_with_stdio(0);cin.tie(0);

    ll T;cin>>T;
    while(T--){
        ll n;cin>>n;
        ll l=1,r=n+1,ans=-1;
        while(l<r){
            ll mid=(l+r)>>1;
            if(mid<pow((n+mid-1)/mid,2)){
                ans=mid;
                l=mid+1;
            }else {
                r=mid;
            }
        }
        cout<<min(ans+2,n*n)<<"\n";
    }
    return 0;
}