Joker - AtCoder agc044_b - Virtual Judgehttps://vjudge.net/problem/AtCoder-agc044_b https://vjudge.net/problem/AtCoder-agc044_b
https://vjudge.net/problem/AtCoder-agc044_b
思路分析
每次有一个人离开,这个人的坐标是(x,y),意味着其上下左右可能有人,通过(x,y)离开的怒气值比当前这个人的怒气值小,而新的这个怒气值减小的人,其上下左右的人中,也有可能有人通过这个新的人离开, 会让自身怒气值减小,如此反复,直到没有人的怒气值能够被减小
实现方法
使用occ[x][y](0-没有被占据 1-被占据)表示这个点有没有被占据,使用h[x][y]表示这个点的怒气值,则其周围的点通过这个点离开,其怒气值为occ[x][y]+h[x][y]
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=505;
int h[maxn][maxn],occ[maxn][maxn];
int n;
int dx[5]={-1,1,0,0},dy[5]={0,0,-1,1};
void dfs(int x,int y){
int z=occ[x][y]+h[x][y];
for(int i=0;i<4;i++){
int nx=x+dx[i],ny=y+dy[i];
if(z<h[nx][ny]){
h[nx][ny]=z;
dfs(nx,ny);
}
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
occ[i][j]=1;
h[i][j]=min(min(i,n-i+1),min(j,n-j+1))-1;
}
}
long long res=0;
for(int i=1;i<=n*n;i++){
int t;cin>>t;
//获取x,y坐标
int x=(t+n-1)/n,y=t%n;
if(y==0) y=n;
res+=h[x][y];
occ[x][y]=0;
dfs(x,y);
}
cout<<res<<"\n";
return 0;
}
实现的细节(如果没有以下疑惑,可以跳过)
Q1.一个点会不会被反复考虑:从一个点出发,延展出的其他怒气值减小的点,都是经过这个点的,其怒气值只能增加或相等,不会减少,所以一个点不会被反复考虑
Q2.超出边界的点(x=0 y=0 x>n y>n):其h[x][y]被全局变量初始化为0,因此不可能被考虑
复杂度分析
每个点最多被更新其初始状态(没有任何人离开)下的怒气值次,比如一个点初始的怒气值是5,每次更新至少-1,那这个点最多减5次变为0,其最多被考虑5次
所以,复杂度上限可以被估计为,初始状态每个人的怒气值的和,经过计算,为n^3数量级
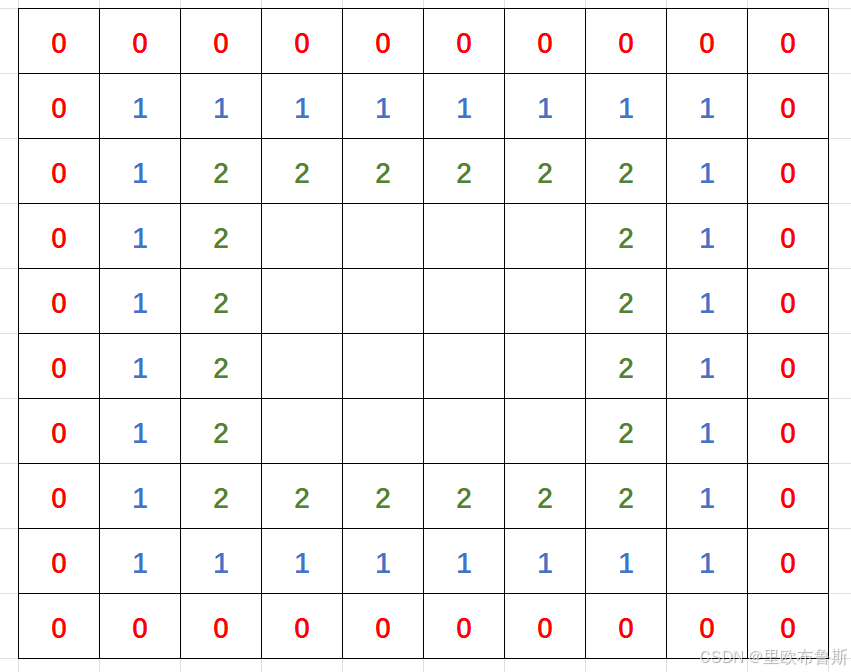
计算方法:初始状态,最外周的人怒气值为0,次外周的人怒气值为1,依次累加




















 1040
1040

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








