郑州大学北区院赛题解（CEJ）

最新推荐文章于 2025-11-25 00:06:26 发布

原创最新推荐文章于 2025-11-25 00:06:26 发布 · 374 阅读

6 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++

文章介绍了第二类斯特林数的计算方法，AC代码实现，以及涉及思维题中的优化策略，如调整序列求和问题和使用DFS解决特定问题，同时提到了线段树在维护前缀和中的应用和二分查找的提及。

1.第二类斯特林数：

把n!去掉就是一个第二类斯特林数，具体可以看看我上次写的牛客寒假训练营1。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
long long n,m,nxt[1200],mod=1e9+7;
long long qpow(long long n,long long x){
	int num=1;
	while(x){
		if(x&1) num=num*n%mod;
		n=n*n%mod;
		x>>=1;
	}
	return num;
}
void solve(){
	cin>>n>>m;
	if(m>n){
		 cout<<0;
		 return;
	}
	long long ans=0;
	nxt[0]=1;
	for(int i=1;i<=m;i++) nxt[i]=nxt[i-1]*i%mod;
	for(int i=0;i<=m;i++){
		ans=(ans+qpow(-1,m-i)*qpow(i,n)%mod*qpow(nxt[i],mod-2)%mod*qpow(nxt[m-i],mod-2)%mod)%mod;
	}
	cout<<ans*nxt[m]%mod;
}
int main(){
	std::ios::sync_with_stdio(false);
    solve();
    return 0;
}

2.思维题：

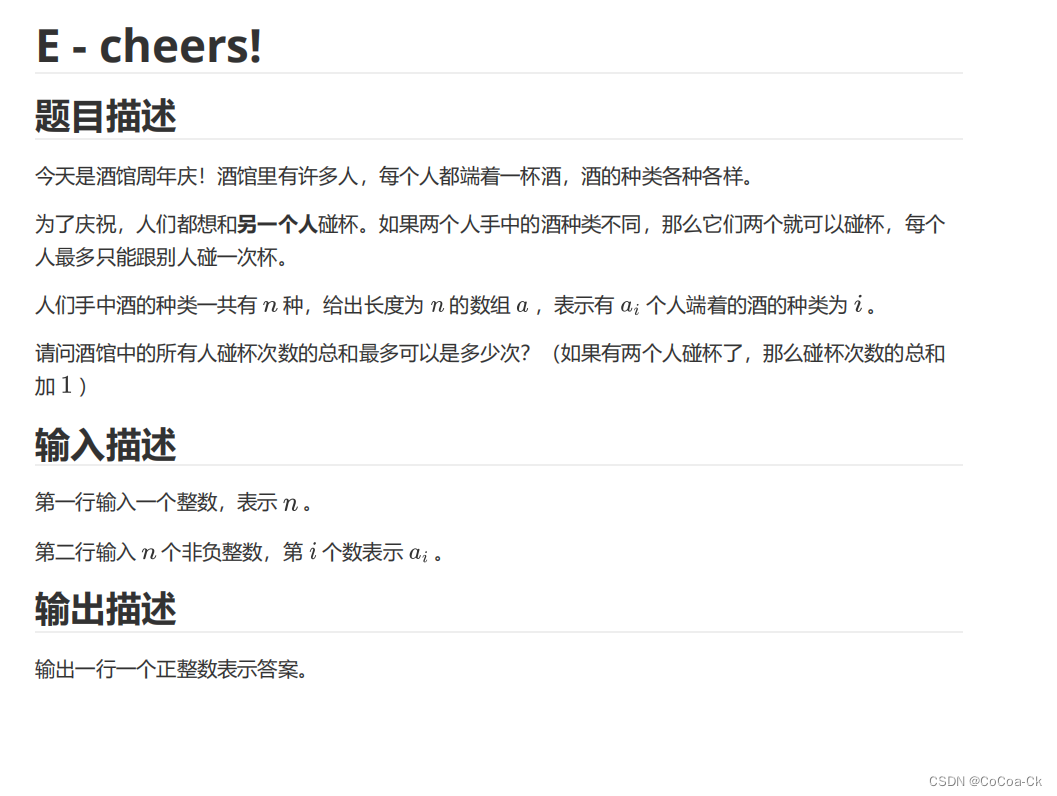
我们看看3，6，7，11的例子，首先，我们知道最好的情况是所有值加起来/2（下取整），对于这个例子，我们可以让11-3=8变成6,7,8,对于6只要先把8-1=7变成5,7,7,然后让把5尽可能的平均分配给7即可。

让我们考虑一下边界情况，即3，6，7，x，x-3-6>7，即x大于sum的一半时就无法使每一个都有匹配，此时的值就是3+6+7了。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,ans,x,sum,max1;
void solve(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		max1=max(max1,x);
		sum+=x;
	}
	if(max1*2>sum) ans=sum-max1;
	else ans=sum/2;
	cout<<ans;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	solve();
}

3.DFS

4^10*10的复杂度可以接受，于是DFS，接下来就是一堆判断了，下面是代码（貌似好像DBCCDCBACD也没有问题）：

#include<bits/stdc++.h>
using namespace std;
int a[15],num[15];
bool ww[5];
bool check(){
	//1
	if(a[1]==1&&a[8]!=1) return 0;
	if(a[1]==2&&a[2]!=2) return 0; 
	if(a[1]==3&&a[4]!=3) return 0;
	if(a[1]==4&&a[5]!=4) return 0;
	//2
	if(a[2]==1&&a[3]!=a[5]) return 0;
	if(a[2]==2&&a[2]!=a[7]) return 0;
	if(a[2]==3&&a[5]!=a[6]) return 0;
	if(a[2]==4&&a[9]!=a[10]) return 0;
	//3
	if(a[3]==1&&num[a[3]]!=2) return 0;
	if(a[3]==2&&num[a[3]]!=5) return 0;
	if(a[3]==3&&num[a[3]]!=4) return 0;
	if(a[3]==4&&num[a[3]]!=6) return 0;
	//4
	if(a[4]==1&&a[2]!=3) return 0;
	if(a[4]==2&&a[2]!=4) return 0;
	if(a[4]==3&&a[2]!=2) return 0;
	if(a[4]==4&&a[2]!=1) return 0;
	//5
	if(a[5]==1&&a[2]!=1) return 0;
	if(a[5]==2&&a[4]!=2) return 0;
	if(a[5]==3&&a[1]!=3) return 0;
	if(a[5]==4&&a[10]!=4) return 0;
	//7
	int cc=0;
	for(int i=2;i<=10;i++){
		if(a[i]==a[i-1]) cc++;
	}
	if(a[7]==1&&cc!=2) return 0;
	if(a[7]==2&&cc!=1) return 0;
	if(a[7]==3&&cc!=4) return 0;
	if(a[7]==4&&cc!=0) return 0;
	//8
	memset(ww,0,sizeof(ww));
	for(int i=2;i<=6;i++){
		ww[a[i]]=1;
	}
	int yy=0;
	for(int i=1;i<=4;i++){
		if(!ww[i]){
			yy=i;
			break;
		}
	}
	if(a[8]==1&&yy!=1) return 0;
	if(a[8]==2&&yy!=2) return 0;
	if(a[8]==3&&yy!=3) return 0;
	if(a[8]==4&&yy!=4) return 0;
	//9
	int fk=0;
	for(int i=1;i<=4;i++){
		if(num[i]<4) fk++;
	}
	if(a[9]==1&&fk!=1) return 0;
	if(a[9]==2&&fk!=2) return 0;
	if(a[9]==3&&fk!=3) return 0;
	if(a[9]==4&&fk!=4) return 0;
	//10
	if(a[10]==1){
		if(a[4]!=a[9]||a[9]!=a[10]||a[3]==a[4]) return 0;
	}
	if(a[10]==2){
		if(a[3]!=a[9]||a[9]!=a[10]||a[3]==a[4]) return 0;
	}
	if(a[10]==3){
		if(a[4]!=a[10]||a[3]!=a[10]||a[9]==a[4]) return 0;
	}
	if(a[10]==4){
		if(a[4]!=a[9]||a[9]!=a[3]||a[3]==a[10]) return 0;
	}
	return 1;
}
void dfs(int cnt){
	if(cnt==11){
		if(check()){
			for(int i=1;i<=10;i++) cout<<(char)(a[i]+'A'-1)<<endl;
		}
		return;
	}
	for(int i=1;i<=4;i++){
		a[cnt]=i;
		num[i]++;
		dfs(cnt+1);
		num[i]--;
	}
	return;
}
int main(){
	dfs(1);
}