①原版(实用解法)
class Solution {
public:
int Fibonacci(int n) {
int res[2] = { 0,1 };
if (n < 2)
return res[n];
int fib_N_minus_One = 1;
int fib_N_minus_Two = 0;
int fib_N = 0;
for (int i = 2; i <= n; i++) {
fib_N = fib_N_minus_One + fib_N_minus_Two;
fib_N_minus_Two = fib_N_minus_One;
fib_N_minus_One = fib_N;
}
return fib_N;
}
};
②原版(普通法)
缺点:计算量过大,逻辑上二叉树含大量重复结点
int Fibonacci(int n) {
if (n <= 0)
return 0;
if (n == 1)
return 1;
else
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
结果比较:
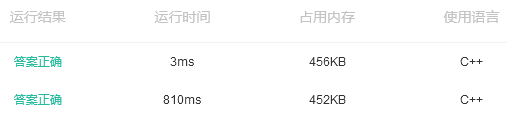
时间复杂度上差距还是挺明显的





 这篇博客探讨了两种不同的C++实现斐波那契数列的方法:一种是实用解法,利用数组降低计算量;另一种是递归解法,存在大量重复计算。通过对比,突显了实用解法在时间复杂度上的优势,避免了不必要的计算和内存浪费。
这篇博客探讨了两种不同的C++实现斐波那契数列的方法:一种是实用解法,利用数组降低计算量;另一种是递归解法,存在大量重复计算。通过对比,突显了实用解法在时间复杂度上的优势,避免了不必要的计算和内存浪费。
















 791
791

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








