剑指offer-刷题笔记-简单题-JZ42 连续子数组的最大和

剑指offer-刷题笔记-简单题-JZ42 连续子数组的最大和

重点记录一下动态规划的方法，目前使用动态规划的方法共做了两道题，还有一个是JZ10 斐波那契数列，方法就是清楚每一个最优的子结构，比如斐波那契数列，f(1)=1,f(2)=1,f(3)=f(2)+f(1),f(n)=f(n-1)+f(n-2),并且最优子结构之间存在对应关系，将最优子结构存储，然后用的时候再取出。

动态规划解决JZ10 斐波那契数列

class Solution {
public:
int Fibonacci(int n) {
		
		int f[50];
		f[1] = 1;
		f[2] = 1;
		for (int i =3; i <= n;i++)
		{
			f[i] = f[i-2]+ f[i-1];
		}
		return f[n];
	}
};

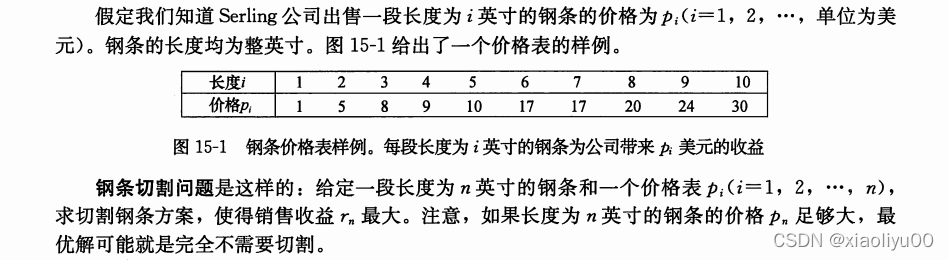
算法导论中有一道切割钢条的问题，也适用于动态规划，可以计算得到最大收益为f(1) = 1,f(2)=5,f(3)=8,f(4)=10,最大收益即最大子结构，最大收益如何找到呐，就是两种，要么切开为前面的最大收益的和f(i)+f(j) i+j = n，要幺不切开为p(n)，则对应关系为f(1) = max(p(1)),f(2) = max(p(2),f(1)+f(1)),f(3) = max(p(3),f(1)+f(2)),f(4) = max(p(4),f(2)+f(2),f(1)+f(3)),注意这里不要再将f(4)=f(1)+f(2)+f(1)或者其他的，因为每次取得都是前面最大收益，这样对应关系也有了，f(n)=max(p(n),f(i)+f(j)) i+j=n

动态规划解决切割钢条

 int buttom_up_cut(vector<int> p)
	{
		int size = p.size()-1;
	  	vector<int> f(size+2);
	  	f.pushback(p[0]);
		for(int i=1;i <= size;i++)
		{
			int q=-1;
			for(int j=1;j<=i;j++)
			{
				q = max(q, p[j-1]+f[i-j]);//为了保证最后的是最大值，不断更新q
			}
			f.pushback(q);
		}
		return f[size];
	}

版本1

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        //int result;
        if(array.size() == 1)
        {
            return array[0];
        }else{
            int count = array[0];//从第一个数字开始累加 
            int temp = count;//前一个最大值
            for(int i = 1;i<array.size();i++)
            { 
                if(count < 0)
                {
                    count = array[i];//序列第一个位置改变
                }
                else{
                    count += array[i];//不断累加
                }
                temp = temp > count ? temp : count;//判断加了元素之后最大值是否变小，正对最后一个数字为是负数
            }
            return temp;
        }

        //return result;
        
    }
};

同样的求连续子数组的最大和也可以用动态规划，即保证每一个子数组达到最优结构，再找到对应关系，类似的关系，f(1) = max(p(1),p(1)+f(0)),f(2) = max(p(2),p(2)+f(1)),f(i)=max(p(i),p(i)+f(i-1)),也就是说当前最有子结构应该为max(当前值，当前值+前一个最优子结构)

版本2-动态规划

class Solution {
public:
    int FindGreatestSumOfSubArray(vector<int> array) {
        int sz = array.size();
        vector<int> dp(sz+1, 1);
        dp[0] = 0; // 表示没有元素
        int ret = array[0];
        for (int i=1; i<=sz; ++i) {
            dp[i] = max(array[i-1], dp[i-1]+array[i-1]);
            ret = max(ret, dp[i]);//为了保证最后的是最大值，不断更新
        }
        return ret;
    }
};