CCF 201312-3 最大的矩形 C++ 没全懂

最新推荐文章于 2024-08-23 14:47:43 发布

原创最新推荐文章于 2024-08-23 14:47:43 发布 · 211 阅读

0 ·

CC 4.0 BY-SA版权

C++笔记专栏收录该内容

26 篇文章

订阅专栏

这篇博客介绍了两种不同的算法来解决二维数组（高度数组）中找到最大矩形面积的问题。第一种是暴力解法，对每个矩形作为左边界，遍历并更新右边界，计算面积并保存最大值。第二种方法利用了栈，遇到小于栈顶元素高度的值时停止入栈，然后依次出栈计算面积，直至找到符合条件的矩形。这两种方法分别具有O(n^2)和O(n)的时间复杂度。

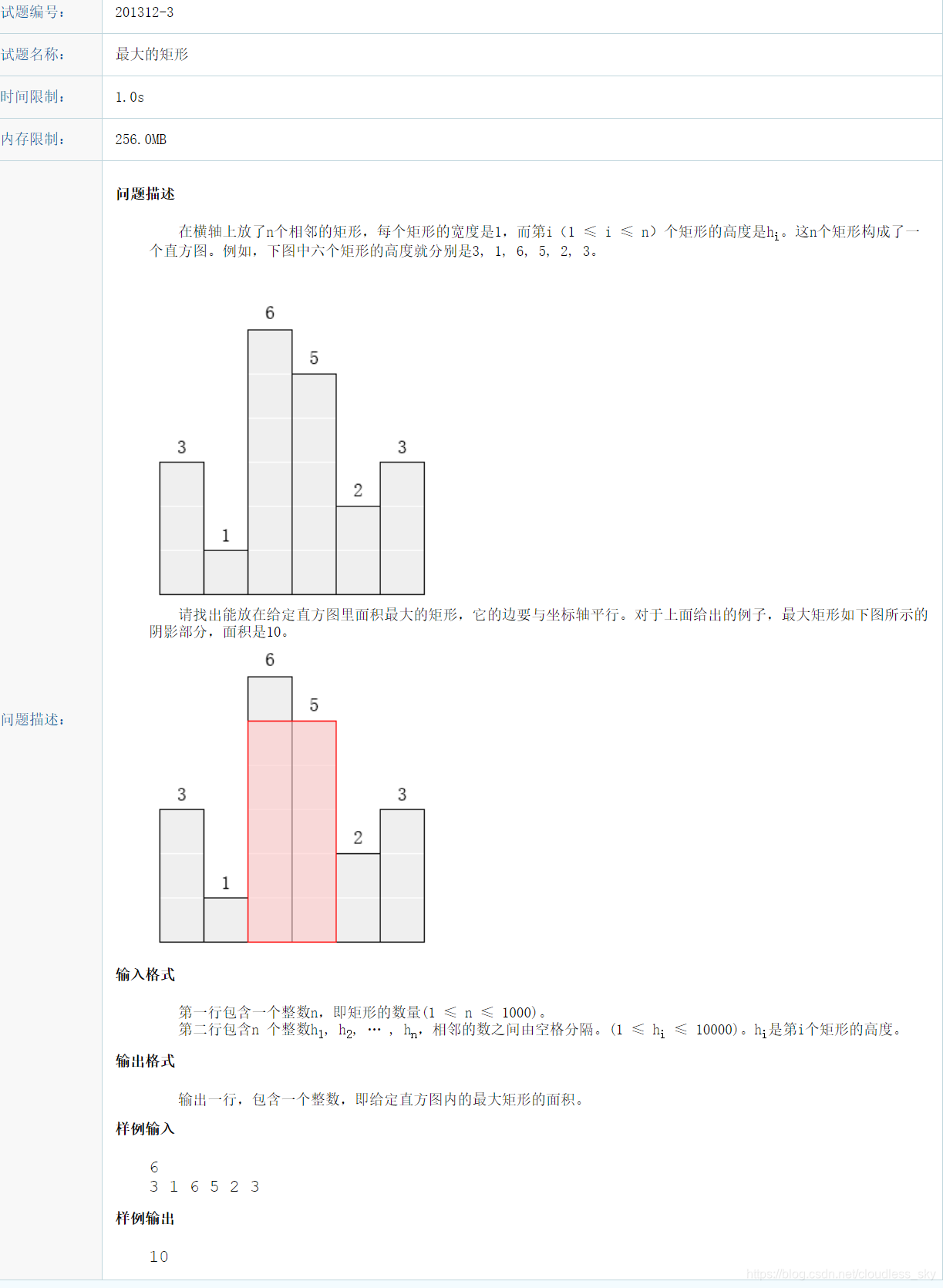
在这里插入图片描述

暴力解法100分：对于每个矩形都作为一次左边界，依次加入右边的矩形，并根据后面矩形的高度调整矩形的宽，并比较当前矩形的面积是否变大。

//矩形最大面积暴力解法 
#include <iostream>
using namespace std;
int main()
{
	int n,low,ans=0;
	cin >> n;
	int a[n];
	for(int i=0;i<n;i++)
	{
		cin >> a[i]; 
	}
	for(int i=0;i<n;i++)
	{
		low=a[i];
		for(int j=i+1;j<n;j++)
		{
			if(a[j]<low)   low=a[j];
			if(low*(j-i+1)>ans) ans=low*(j-i+1);
		} 
	} 
	cout << ans << endl;
	return 0;
}

复杂度为0(n)的算法：遇到比栈顶元素小的元素就停止入栈，然后依次出栈检查栈中元素，如果

#include <iostream>
#include <algorithm>
#include <stack>
using namespace std;

int h[1010];		//高度数组 
int main(){
	int num, temp, wide;
	int ans=0; 	
	
	cin>>num;		//输入矩形数量 矩形高度 
	for(int i=0;i<num;++i)
		cin>>h[i]; 
	h[num] = 0;		//加一个0边界使最终计算高度最小值对应的面积
	stack<int> st;	//高度栈
	for(int i=0; i <= num; ++i){
		//高度大于栈顶元素入栈；小于计算面积；等于pass 
		if(st.empty() || (h[st.top()] <h[i]))	
			st.push(i);
		else if(h[st.top()] > h[i]){
			//循环计算面积直到满足条件 
			while( !st.empty() && (h[st.top()] >= h[i])){
				temp = st.top();
				st.pop();
				//计算宽度及面积 
				wide = st.empty()? i: i-st.top() -1;	
				ans = max(ans, h[temp]*wide);
			}
			st.push(i);
		}
	} 
	cout<<ans<<"\n";
	return 0;
}

或者

/* CCF201312-3 最大的矩形 */
 
#include <iostream>
#include <stack>
 
using namespace std;
 
const int N = 1000;
int h[N+1];
 
int main()
{
    int n, ans=0, area, temp;
 
    // 输入数据
    cin >> n;
    for(int i=0; i<n; i++)
        cin >> h[i];
    h[n] = 0;
 
    // 计算最大矩形面积
    stack<int> s;
    for(int i=0; i<=n; i++) {
        if (s.empty() || h[s.top()] < h[i])
            s.push(i);
        else {
            temp = s.top();
            s.pop();            //弹出
            area = h[temp] * (s.empty() ? i : i - s.top() - 1);
            if (area > ans)
                ans = area;
            --i;
        }
    }
 
    // 输出结果
    cout << ans << endl;
 
    return 0;
}

大佬解法没懂，日后再看吧。