左叶子之和

原创于 2020-12-29 15:45:18 发布 · 197 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二叉树 #算法 #leetcode

C++笔记专栏收录该内容

26 篇文章

订阅专栏

博客围绕计算给定二叉树的所有左叶子之和展开，以力扣（LeetCode）题目为例，给出示例。介绍了先序递归思路，强调判断左叶子的重点，还指出错误写法会增加耗时，最后提及非递归算法。

计算给定二叉树的所有左叶子之和。

示例：
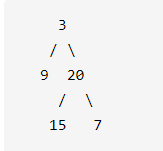
在这里插入图片描述

在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/sum-of-left-leaves
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
思路：
先序递归。这道题的重点在于如何判断是左边的叶子。如果左孩子不空且它是叶子节点就加和，否则如果左孩子空则去遍历右孩子，如果左孩子不空但是不是叶子节点就继续遍历左右孩子。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {    
public:
    int sumOfLeftLeaves(TreeNode* root) {
        int midValue=0;//注意midValue的定义位置
        if(root==NULL) return 0;
        if(root->left && root->left->left==NULL && root->left->right==NULL)
        {
            midValue+= root->left->val;           
        }
        midValue+=sumOfLeftLeaves(root->left);
        midValue+=sumOfLeftLeaves(root->right);
        return midValue;

    }
};

不要写成 return midValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);这样的话耗时多。
非递归算法：


class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        stack<TreeNode*> st;
        if (root == NULL) return 0;
        st.push(root);
        int result = 0;
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
                result += node->left->val;
            }
            if (node->right) st.push(node->right);
            if (node->left) st.push(node->left);
        }
        return result;
    }
};

作者：carlsun-2
链接：https://leetcode-cn.com/problems/sum-of-left-leaves/solution/404-zuo-xie-zi-zhi-he-di-gui-yu-fei-di-gui-fang-fa/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。