Now we have entered in the era of "big data". We have accumulated so many data that we can't all information from them. On the other hand, so many data may form noise to separate you from truth. So to learn potential pattern from given data, we need to pre-train and filter data.
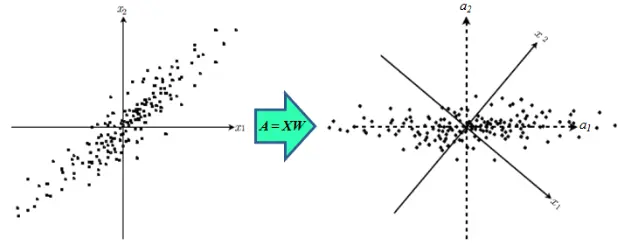
Now given n samples, x_1,...x_n, in d-dim. If d is very large which means x has many features, then we may do some feature selection before we start to learn. One way is to do principal component analysis for these samples. For example, if all sample points on plane almost lie on one straight line, then that straight line can be seen as 1-dim principal component of data.
Zero-dimension representation by PCA
If we use only one vector to represent all sample points, then the vector must be the average of all sample points.
one-dim representation by PCA
If we want to find one line close to all sample points and use projections to approximate sample points, then the line must go through sample average point.
To find a d'-dim PC of sample points, it is equivalent to solve
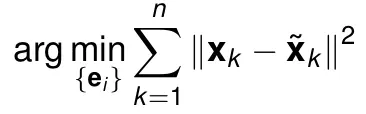
The vectors e_i all have length 1. So use Lagrange optimization to solve. Then we can get all e_i are eigenvectors of scatter matrix S, that is
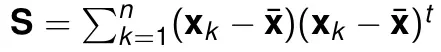
S is n*n matrix which is real and symmetric. Then its eigenvectors are orthogonal and its eigenvalues are nonnegative. The eigenvalues corresponding e_1,...,e_d' are the first d' maximal eigenvalues of S. And the squared error above has an explicit expression by information of S, that is sum of eigenvalues except first d' maximal eigenvalues. And since eigenvectors are orthogonal, they can be used to represent d'-dim subspace center at sample average point.








 本文介绍了主成分分析(PCA)的基本原理及应用。PCA是一种常用的数据降维方法,通过将原始高维数据映射到低维空间来简化数据集,同时尽可能保留数据的重要特征。文章详细解释了如何通过求解散射矩阵的特征向量来实现PCA,并给出了不同维度下PCA表示的具体形式。
本文介绍了主成分分析(PCA)的基本原理及应用。PCA是一种常用的数据降维方法,通过将原始高维数据映射到低维空间来简化数据集,同时尽可能保留数据的重要特征。文章详细解释了如何通过求解散射矩阵的特征向量来实现PCA,并给出了不同维度下PCA表示的具体形式。
















 791
791

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








