#include <bits/stdc++.h>
#define eps 1e-6
using namespace std;
int n;
double x[1010],y[1010],h[1010],dis[1010];
bool vis[1010];
double d(int i,int j){return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));}
bool check(double l){
double z=0.0;
memset(vis,0,sizeof(vis));
vis[1]=1,dis[1]=0; //从一号点开始搜
for(int i=2;i<=n;i++)dis[i]=d(1,i)-l*fabs(h[1]-h[i]); //一号点到每个点的DIS值
for(int i=1;i<n;i++){ //一共扫N-1轮,即连N-1条边
double mx=-200000000;mx*=10000.0; //记最大DIS值
int mni; //记点
//dis数组存的是当前已连点集中向外连接的点的DIS最大值
//如点集有1,2号点都连向3号点,DIS存的是1,2号点连接3号点中的最大值
for(int j=1;j<=n;j++) if (!vis[j]&&dis[j]>mx) mx=dis[j],mni=j; //得本轮循环DIS最大的点
vis[mni]=1; //标为已访问,即连边,但是其实是点集中谁连过去的并不重要
z+=dis[mni]; //最大生成树累加,每次都是求F表达式的最大值
for(int j=1;j<=n;j++)//从最小点开始往外射出更新最短距离
if (!vis[j]) dis[j]=max(dis[j],d(mni,j)-l*fabs(h[mni]-h[j]));
}
if (z<0) return 0;//如果L太大的话,DIS数组的值会是负值来的
else return 1;
}
int main(){
while(scanf("%d",&n)&&n){
bool flag=0;
for(int i=1;i<=n;i++){
scanf("%lf%lf%lf",&x[i],&y[i],&h[i]);
for(int j=1;j<i;j++) if (h[i]!=h[j]) {flag=1;break;}
}
if (!flag) {printf("0.000\n");continue;}//就怕费用全为0
double l=0,r=200000000;
while(r-l>=eps){
double mid=(l+r)/2;
if (check(mid)) l=mid;
else r=mid;
}
printf("%.3f\n",1.0/r);
}
return 0;
}
个人认为关键:就是最大生成树的时候边权改为F[cnt]表达式
原题是求ABS/DIS=CNT最小值,代码改为求DIS/ABS=CNT最大值
然后令DIS-CNT*ABS0,当F小于0时,CNT更大不存在,当F大于0时,CNT可变大更优
POJ-2728-01
题目大意:平面上有nn个点,每个点上有一个高度h(i)h(i),在两个点之间修建管道所需的费用是|h(i)−h(j)||h(i)−h(j)|,管道的长度是两个点的欧几里得距离,要求一棵生成树使得费用和与管道总长比值最小,求这个最小比值。
Sample Input
4
0 0 0
0 1 1
1 1 2
1 0 3
0
Sample Output
1.000
构造一个函数:![]()
其中F(r)在平面坐标系上体现为一条直线,每一组x[i]都分别唯一地对应一条直线,这些直线的截距均大于等于0、斜率均小于等于0。而这些直线在X轴上的截距就是这一组x求出来的r,而截距的最大值就是我们要求的R。(如下图所示)
个人理解:每次都控制DIS与ABS使得表达式F(R)得到最大值,至于R是落在临界左边还是右边是不归DIS与ABS管的,反正DIS与ABS就是要变成那条最大的直线,像本题不断更新DIS,就是表达式的值变最大,加到最后还是小于零,说明R就是大于临界的,记好:就是往界点走就更优
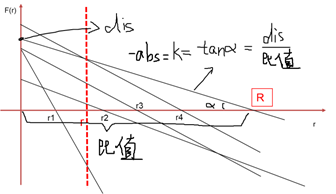
在X轴上面任取一个r,如果至少有一条直线的F(r)>0,那么说明了什么呢?
说明至少还有一条直线与X轴的交点在它的右边,那么这个r一定不是最大值,真正的最大值在它的右边。反之,如果所有的F(r)都小于0,那么真正的最大值在它的左边
那么前面的结论就可以换种说法,因为我只需判断最大的那个F(r)的正负性就行了:
随便取一个r,如果F(r)max>0,则结果R>r,反之若F(r)max<0,则结果R<r。直到找到使F(r)max=0的r,那个r就是我们要找的结果R





 本文探讨了一种解决平面上多个点间构建管道问题的算法,目标是最小化费用与管道总长的比值。通过定义一个特殊函数,将问题转化为求最大生成树的情景,利用迭代逼近的方法找到最优比值。
本文探讨了一种解决平面上多个点间构建管道问题的算法,目标是最小化费用与管道总长的比值。通过定义一个特殊函数,将问题转化为求最大生成树的情景,利用迭代逼近的方法找到最优比值。
















 4991
4991

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








