L*a*b*空间彩色图像加密

CIE L*a*b* 空间中的彩色图像加密

金鑫1,2(B)，陈英雅1,2,葛士明3,张克军1,2,李晓东1,2(B)，李玉珍1,2,4,刘燕1,2,4,郭奎1,2,田雨露1,2,赵庚1,2,张晓坤1,2,和王子仪1,2
1北京电子科技学院，中国北京100070{jinxin,lxd}@besti.edu.cn
2信息安全部重实验室，中国北京100070
3中国科学院信息工程研究所，中国北京 100093
4西安电子科技大学，中国西安710071

摘要

为了在移动互联网时代保护图像存储和传输过程中的内容安全，图像加密在过去几十年中取得了巨大成功。目前，彩色图像加密领域对非 RGB色彩空间（如HSV、YUV和L*a*b*颜色空间）的关注较少。本文提出在信息量较高的通道中采用 high level加密方案，而在信息量较低的通道中采用 lowlevel加密方案。这是首次在CIE L*a*b*颜色空间中进行彩色图像加密。首先，将RGB转换为L*a*b*颜色空间；然后，在L*通道中使用二维Arnold猫映射结合三维Lu混沌映射进行加密；在包含信息较少的a*和b*通道中，则采用较为简单的DNA编码和一维logistic映射的加密方案。实验结果表明，我们的方法在每个通道上与在RGB颜色空间中采用相同加密方案的方法具有相似的加密效果，但耗时更少。此外，我们的方法能够抵抗暴力破解攻击、统计攻击和相关性攻击。

关键词 ：彩色图像加密 · L*a*b* · Chaotic映射 · Selective加密

1 引言

摄像头和智能手机如今已广泛应用于日常生活中。大量图像通过社交网络软件和云存储传输给成千上万的人。2014年8月31日，近500张涉及多位名人的私人照片（大多数为女性，其中许多包含裸露内容）被发布在图片论坛4chan上，随后由其他用户在Imgur、Reddit和Tumblr等网站及社交网络上传播。这些照片据信是通过入侵苹果云服务套件iCloud而获取的。这一事件警示我们，云端中的隐私正面临威胁。此外，一旦政府或军事图像泄露，国家安全将受到侵犯。因此需要图像加密技术，以实现高水平的安全性、完整性、机密性，并防止在不安全信道上的图像存储或传输过程中对敏感信息的未授权访问 [1,3,4]。

当前的图像加密技术主要集中在灰度图像加密[2,5]。RGB色彩空间主导了彩色图像加密方法。对于非RGB色彩空间（如HSV、YUV或L*a*b*颜色空间）的研究则较少。由于红色、绿色和蓝色分量之间具有高度关联性，RGB颜色空间是处理和存储图像数据最广泛使用的色彩空间之一。然而，RGB颜色空间混合了色度和亮度分量，因此无法用于基于色彩准则的色彩分析和分割方法[1]。

如图1所示，大多数非RGB色彩空间具有一个共同特性，即一个或两个通道所包含的视觉识别信息多于其他通道。这一特性使我们能够在信息量较大的通道中使用高级加密方案，而在信息量较小的通道中使用低级加密方案。

L*a*b*颜色空间是一种对立色空间，其中L*表示明度，a* 和b*表示对立色维度，其基于非线性压缩（例如CIE XYZ颜色空间）的坐标。与RGB颜色空间相比，L*通道对颜色分量更加独立，并且在明度方面更接近人类感知[6]。人们可以从L*通道轻松识别出Lena图像，但从a*和b*通道几乎无法获取任何信息。

本文首次在CIE L*a*b*颜色空间中进行彩色图像加密。首先，我们将 RGB转换为L*a*b*颜色空间。在包含更多信息的L*通道中，采用二维Arnold 猫映射和三维Lu混沌映射进行处理；而在信息量较少的a*和b*通道中，则采用较为简单的DNA编码和一维logistic映射加密方案。本研究中的方法已在若干图像上进行了测试，并表现出良好的效果。实验结果表明，我们的方法在与对 RGB颜色空间每个通道都执行相同方案的方法获得相近效果的同时，耗时更少。此外，我们的方法能够抵御暴力破解攻击、统计攻击和相关性攻击等多种攻击。

2 以前的工作

混沌的特定性质，如对初始条件和系统参数的敏感性、伪随机性、遍历性等，使得混沌动力学成为传统加密算法的一种有前景的替代方案。这些内在特性直接关联了香农著作中提出的加密特性——混淆与扩散。由于高维混沌系统具有更高的复杂性，因此更适用于设计安全的图像加密方案。一些基于低维混沌映射的密码系统存在明显缺陷，例如周期短和密钥空间小[2,9]。

张等人 [5]提出了一种利用DNA编码和一维logistic映射的灰度图像加密方法。然而，在2014年，赫尔马西等人 [10]指出该[5]方法不可逆，即只能对明文图像进行加密，且在已知密钥的情况下无法对密文图像进行解密。我们向 DNA加法中添加了一个随机矩阵，使加密过程可逆。

与我们工作最相似的是马迪等人 [1]。他们提出了一种在YCbCr颜色空间中的彩色图像加密方法。在Y通道中，先进行Arnold猫映射，然后使用三维逻辑斯蒂映射。Cb和Cr通道则直接输入到三维逻辑斯蒂映射系统中。本文中，我们提出了一种在L*a*b*颜色空间中的彩色图像加密方法。L*a*b*颜色空间是一种对立色空间，其中L*表示明度，a*和b*表示对立色维度，其基于非线性压缩（例如CIE XYZ颜色空间）的坐标。L*、a*和b*的非线性关系旨在模拟人眼的非线性响应。此外，L*a*b*颜色空间中各分量的均匀变化旨在对应于感知颜色的均匀变化，因此L*a*b*中任意两种颜色之间的相对感知差异可以通过将每种颜色视为一个三维空间中的点（三个分量：L*、a*、b*），并计算它们之间的欧几里得距离来近似[6]。

3 预备知识

我们采用了一种低维混沌映射：一维logistic映射，以及两种高维混沌映射：二维 Arnold猫映射和三维Lu映射。

3.1 一维逻辑斯蒂映射

简单而高效的 一维logistic映射 定义如下：

$$
x_{n+1} = \mu x_n (1 - x_n)
$$

其中 $3.569945672… < \mu \leq 4$, $0 \leq x_n \leq 1$，$n = 0, 1, 2, …$

3.2 二维Arnold猫映射

在数学中，阿诺德猫映射是一种从环面到自身的混沌映射，以弗拉基米尔·阿诺德的名字命名，他在20世纪60年代使用一张猫的图像演示了其效果，因此得名 [7]。Arnold猫映射用于对彩色图像的像素进行像素置乱，以增强密码系统的安全性。二维Arnold猫变换不改变图像像素的值，仅对图像数据进行置乱，其图像加密公式见式(2)，图像解密公式见式(3)。

$$
\begin{bmatrix}
X’ \
Y’
\end{bmatrix}
=
\begin{bmatrix}
1 & p \
q & pq + 1
\end{bmatrix}
\begin{bmatrix}
X \
Y
\end{bmatrix}
\mod 256
\quad (2)
$$

$$
\begin{bmatrix}
X \
Y
\end{bmatrix}
=
\begin{bmatrix}
1 & p \
q & pq + 1
\end{bmatrix}^{-1}
\ast
\begin{bmatrix}
X’ \
Y’
\end{bmatrix}
\mod 256,
\quad (3)
$$

其中 $p$ 和 $q$ 表示正的密钥。 $X, Y$ 是图像像素置乱前的原始位置。 $X’, Y’$ 是图像像素置乱后的新位置。

3.3 三维Lu映射

Lu映射是一种三维混沌映射。它由公式(4)描述：

$$
\begin{cases}
\dot{x} = a(y - x) \
\dot{y} = -xz + cy \
\dot{z} = xy - bz
\end{cases}
\quad (4)
$$

其中$(x, y, z)$为系统轨迹。$(a, b, c)$为系统参数。当$a= 36, b= 3, c= 20$时，系统包含奇异吸引子并处于混沌状态。给定Lu映射的初始值 $x_0, y_0, z_0$ ，令系统迭代 $N \times N$次，每次生成三个序列值。这些序列具有混沌信号的相同特性，即随机性、遍历性和对初值的敏感性，因此可用于图像加密[8]。

4 彩色图像加密 in L*a*b*

在本节中，我们描述了在CIE L*a*b*颜色空间中提出的彩色图像加密方法。如图2所示，首先我们将平面图像从RGB颜色空间转换到L*a*b* 色彩空间。然后使用高维混沌映射对信息丰富的L*通道进行加密。对于信息较少的a*和b*通道，则采用低维混沌映射进行加密，以实现高效计算。

4.1 色彩转换

L* 坐标范围为 0 到 100。a* 和 b* 坐标的可能范围与所转换的色彩空间无关，因为以下转换使用来自 RGB 的 X 和 Y。a* 和 b* 通道的范围为 −128 到 127。在使用混沌映射和 DNA 编码进行加密时，我们将 L*、a* 和 b* 的三个通道全部转换为 0 到 255 的范围（8位）。

4.2 L*通道

在L*通道中，我们采用了二维和三维混沌映射。二维Arnold猫映射用于图像像素的置乱，三维Lu映射用于图像像素的扩散。

图像置乱 。 不同的迭代次数会产生不同的置乱结果。对于分辨率为 $256 \times 256$的灰度图像，超过6次迭代即可获得良好的置乱效果。然而，经过64次迭代后，由于Arnold猫映射的周期性，结果图像会与原始平面图像相同。不同的图像尺寸具有不同的周期。Arnold猫映射的周期性使得置乱的安全性降低。因此，在下一步中，我们利用三维Lu映射对置乱结果进行扩散，以增强安全性。

图像扩散 。 我们使用三维Lu映射对置乱结果进行扩散。通过Lu映射改变每个像素值的步骤如下 [9]：

• 给定Lu映射的初始值 $x_0, y_0, z_0$，令系统迭代 $N \times N$次，每次生成三个序列值。
• 取这三个值的小数部分，将三个小数部分的第四位合并，构成一个新的整数 A。
• 将 $A \mod 256$的结果转换为二进制。图像的灰度值范围在0–255之间，因此 $A \mod 256$的结果必然在此范围内。
• 将经过猫映射加密后的值转换为二进制，并对两个二进制值进行异或运算，共进行 $N \times N$次。
• 将上述步骤的结果再次转换为十进制。返回二维图像，并完成第二次加密。

4.3 A*和B*通道

首先，a*或b*通道通过DNA编码[5]进行编码。然后，我们使用一维logistic映射生成一个与a*或b*相同大小的随机矩阵，并通过DNA加法将其添加到编码结果中。接着，再次使用一维logistic映射生成另一个与a*或b*相同大小的随机矩阵，并将其转换为阈值为0.5的二进制矩阵。当第二个随机矩阵中的对应值为 1时，将DNA加法结果转换为DNA互补结果。最后一步是DNA解码，以获得8 位加密结果。

5 仿真结果

我们使用大量测试图像来测试我们的方法，如图3所示，并使用密钥

$$
\begin{cases}
\text{1D logistic: } \mu_{a^ }= 3.9, x^{a^ } 0= 0.62, \mu {b^ }= 3.99999, x^{b^ } 0= 0.26 \
\text{2D Arnold: } N {\text{iteration}}= 20,p= 1, q= 1 \
\text{3D Lu: }a= 36, b= 3, c= 20, x_0= -6.045, y_0= 2.668, z_0= 16.363
\end{cases}
\quad (5)
$$

对具有不同内容的图像进行了测试。所有加密结果均可使用正确的密钥正确解密为原始测试图像。可以看出，仿真结果非常令人满意。

6 安全性与性能分析

一个设计良好的图像加密方案应能有效抵御各种攻击，例如暴力破解攻击和统计攻击[2]。在本节中，我们以一幅名为婴儿与汽车、大小为 $851\times 851$的示例图像为例，分析所提出加密方法的安全性。我们还将我们的方法（称为L*a*b*方法）与[1]（在下文中称为YUV方法）以及RGB颜色空间中的一种加密方法（在下文中称为RGB方法）进行比较：在R、G和B的每个通道中，采用与本方法在L*通道中所使用的相同加密方案[9]，如图4所示。

6.1 抵抗暴力破解攻击

密钥空间 。 图像加密方案的密钥空间应足够大以抵抗暴力破解攻击，否则可能会在有限时间内通过穷举搜索获得密钥而被破解。在我们的加密方法中，密钥空间如下：

$$
\begin{cases}
\text{1D logistic: } 3.569945672…< \mu \leq 4, x_0 \in[0, 1] \
\text{2D Arnold: } N_{\text{iteration}}> 15,p, q \text{ are positive integers} \
\text{3D Lu: }a= 36, b= 3, c= 20,-40< x_0< 50,-100< y_0< 80, 0< z_0< 140
\end{cases}
\quad (6)
$$

64位双精度数据的精度为 $10^{-15}$，因此密钥空间约为$(10^{15})^8=10^{120} \approx 2^{399}$，远大于AES实际对称加密的最大密钥空间($2^{256}$)。我们的密钥空间足够大，能够抵御暴力破解攻击。

密钥敏感性 。混沌系统对系统参数和初始值极为敏感，微小的差异即可导致解密失败。为了测试图像加密方案的密钥敏感性，我们按如下方式更改密钥：

$$
\begin{cases}
x_0 \text{ from } -6.045 \text{ to } -6.04500000000001 \
x^{a^ }_0 \text{ from } 0.62 \text{ to } 0.62000000000001 \
x^{b^ }_0 \text{ from } 0.26 \text{ to } 0.26000000000001
\end{cases}
\quad (7)
$$

我们使用更改后的密钥来解密 Lena图像 密文图像，如图5所示，而其他密钥保持不变。解密结果及其对应的直方图如图5所示。我们可以看到解密图像与原始Lena图像完全不同。其他密钥的测试结果类似。实验表明，该图像加密方案对密钥非常敏感，也说明其具有较强的抵抗穷举攻击的能力。

6.2 抵抗统计攻击的能力

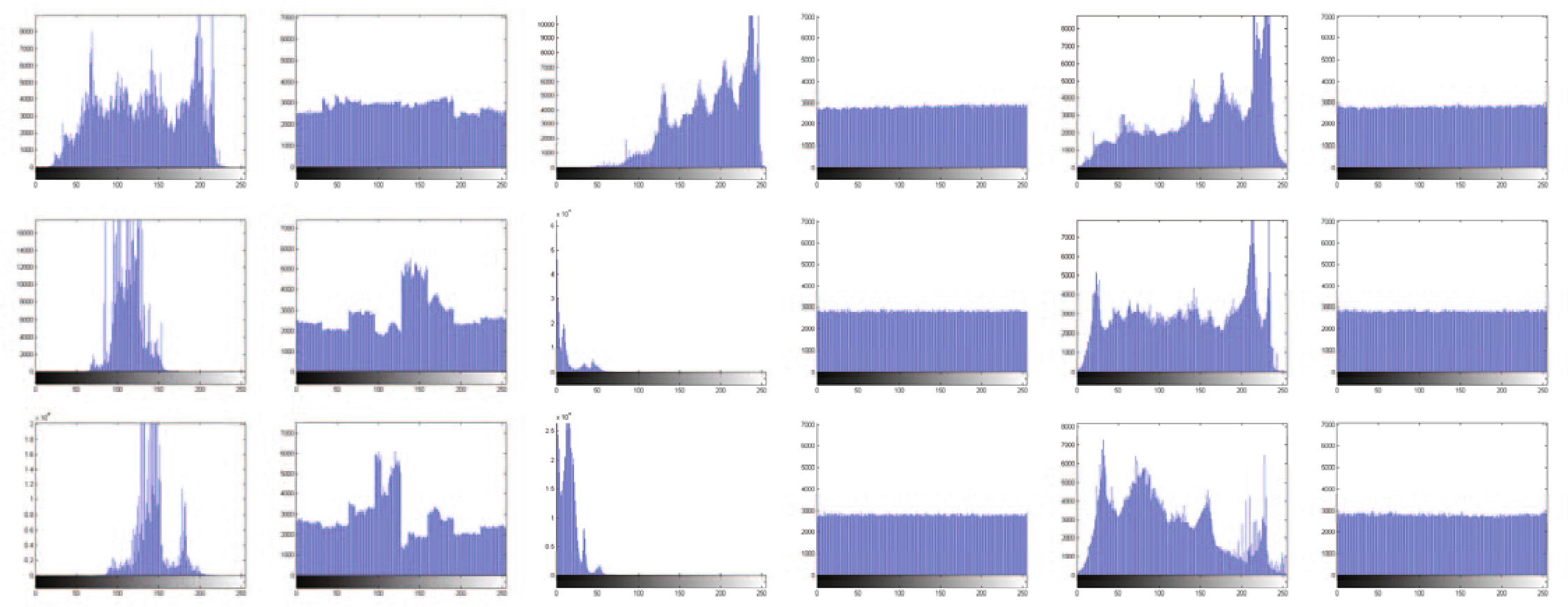
直方图分析 。 直方图用于显示灰度图像像素值的分布情况。密文图像的直方图应足够平坦，否则可能泄露信息，导致统计攻击。这使得通过分析密文图像的统计特性进行仅密文攻击成为可能。图6分别展示了婴儿与汽车图像及其对应密文图像的直方图。比较这两个直方图可以看出，原始婴儿与汽车图像的像素值集中在某些数值上，而其密文图像的直方图则非常均匀，从而使得统计攻击无法实现。

我们还测试了YCbCr方法 [1]和RGB方法 [9]并在图6中展示了它们方法在每个通道的直方图。我们方法的直方图几乎与RGB方法一样平坦，均优于 YCbCr方法。

信息熵 。 信息熵 [2]用于表示随机性，可衡量图像中灰度值的分布情况。像素灰度值分布越均匀，信息熵越大。其定义如下：

$$
H(m)= -\sum_{i=0}^{L} P(m_i) \log_2(m_i)
\quad (8)
$$

其中$m_i$是 $L$级灰度图像的第 $i$个灰度值， $L= 255$。 $P(m_i)$表示 $m_i$在图像中的概率，且 $\sum_{i=0}^{L} P(m_i) = 1$。理想随机图像的信息熵为8，表明信息完全随机。加密后，密文图像的信息熵应接近8，越接近8说明该方案信息泄露的可能性越小。使用我们方法、RGB[9],以及YCbCr方法[1]得到的婴儿与汽车 密文图像的信息熵可总结如下：

$$
\begin{cases}
H(L^ )= 7.9994, H(a^ )= 7.9998, H(b^*)= 7.9997 \
H(R)= 7.9997, H(G)= 7.9998, H(B)= 7.9996 \
H(Y)= 7.9940, H(Cb)= 7.9350, H(Cr)= 7.9196
\end{cases}
\quad (9)
$$

结果表明，我们的方法与RGB方法[9]（熵值接近8）性能相当，且两者均优于 YCbCr方法[1]。

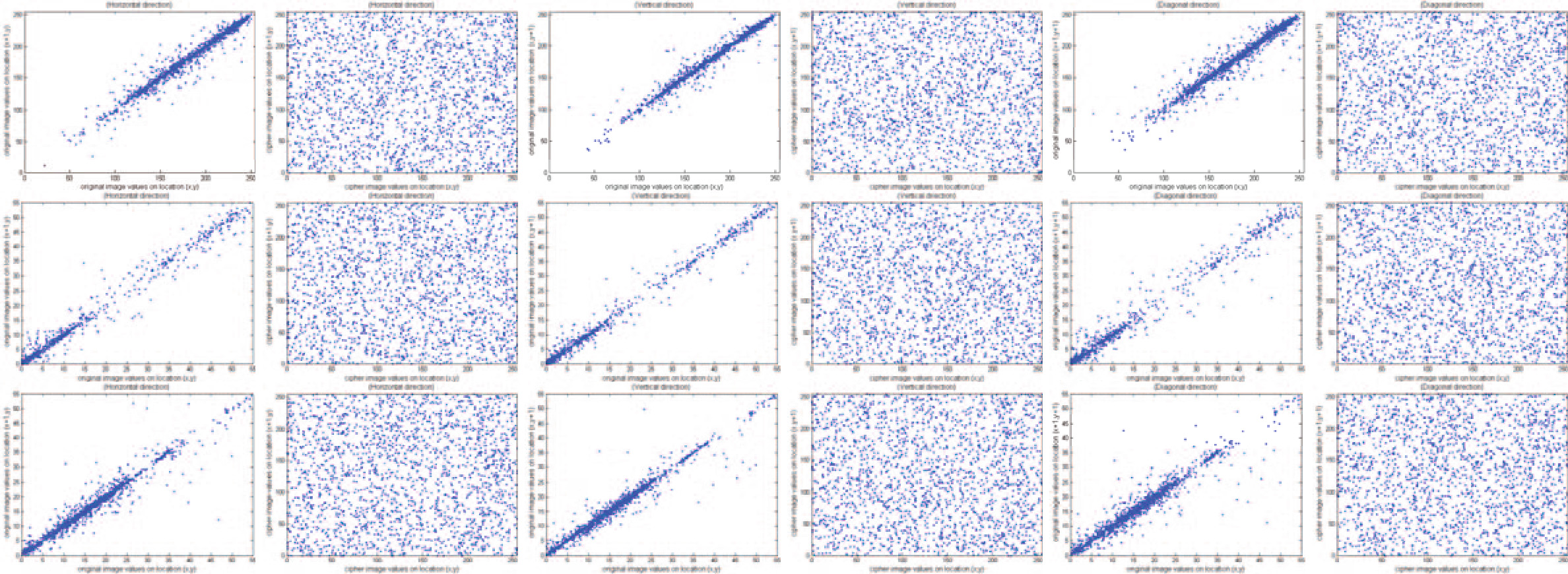
相关性分析 。相关性表示两个随机变量之间的线性关系。在图像处理中，通常用于研究两个相邻像素之间的关系。通常情况下，明文图像中相邻像素的相关性非常高。一个好的加密方案应降低相邻像素之间的相关性，即相邻像素之间的相关性越低，密文图像就越安全。为了测试两个相邻像素的相关性，我们从原始婴儿与汽车图像及其对应的密文图像中，测试了相邻像素的三个方向（水平、垂直和对角线）的相关性。

6.3 加密与解密的速度

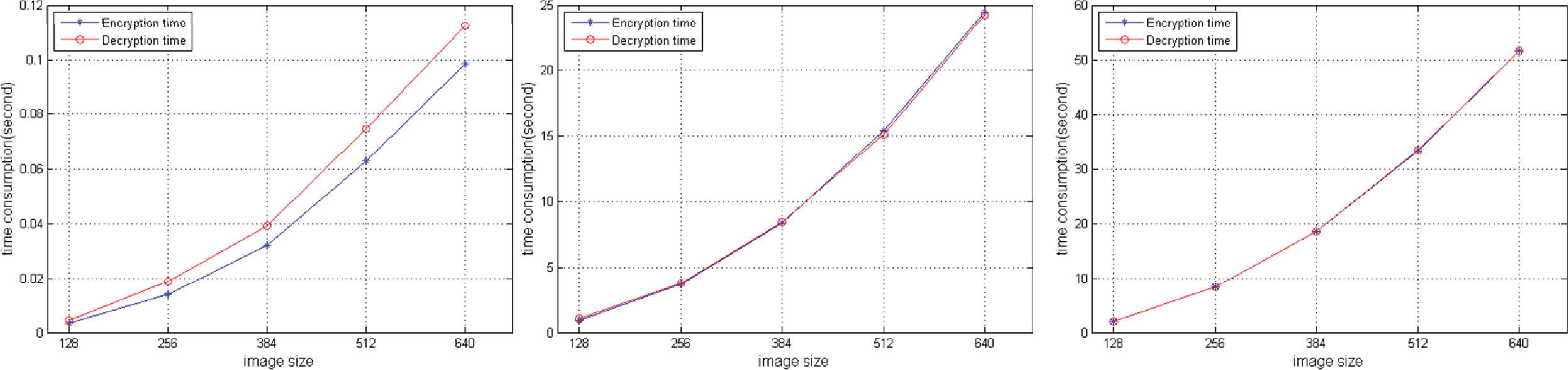
该图像加密方案在配备AMD Athlon(tm) X4 750 四核处理器 3.4GHz和 4.00G内存的个人计算机上通过Matlab实现。记录了不同尺寸图像的加解密耗时。图像尺寸越大，加密和解密所需时间越多。

如图8所示，我们使用YCbCr方法[1],、我们的方法和RGB方法[9]在不同图像尺寸下测试了加密和解密的速度。对比表明，尽管我们的方法在开始和结束时包含了颜色转换，但仍比RGB方法[9]更快。YCbCr方法[1]比我们的方法和RGB方法都更快。然而，如其他实验所示，我们的方法性能与RGB方法[9],相当，且两者均优于YCbCr方法[1]。

7 结论与讨论

在本文中，我们首次在CIE L*a*b*颜色空间中对彩色图像进行加密。在信息丰富的L*通道中，采用了两个高维混沌映射；而在信息较少的a*和b*通道中，使用了一维logistic映射结合DNA编码。因此，我们获得了良好的加密效果以及高效率的彩色图像加密与解密性能。

尽管我们的方法在开始和结束时包含了颜色转换，但它比RGB方法[9]更快。YCbCr方法[1]比我们的方法和RGB方法都更快。然而，如其他实验所示，我们的方法与RGB方法[9],性能相当，且两者均优于YCbCr方法[1]。

在未来工作中，我们将利用YCbCr方法的快速和所提出的L*a*b*方法的良好加密性能。