图搜索算法

图的表示

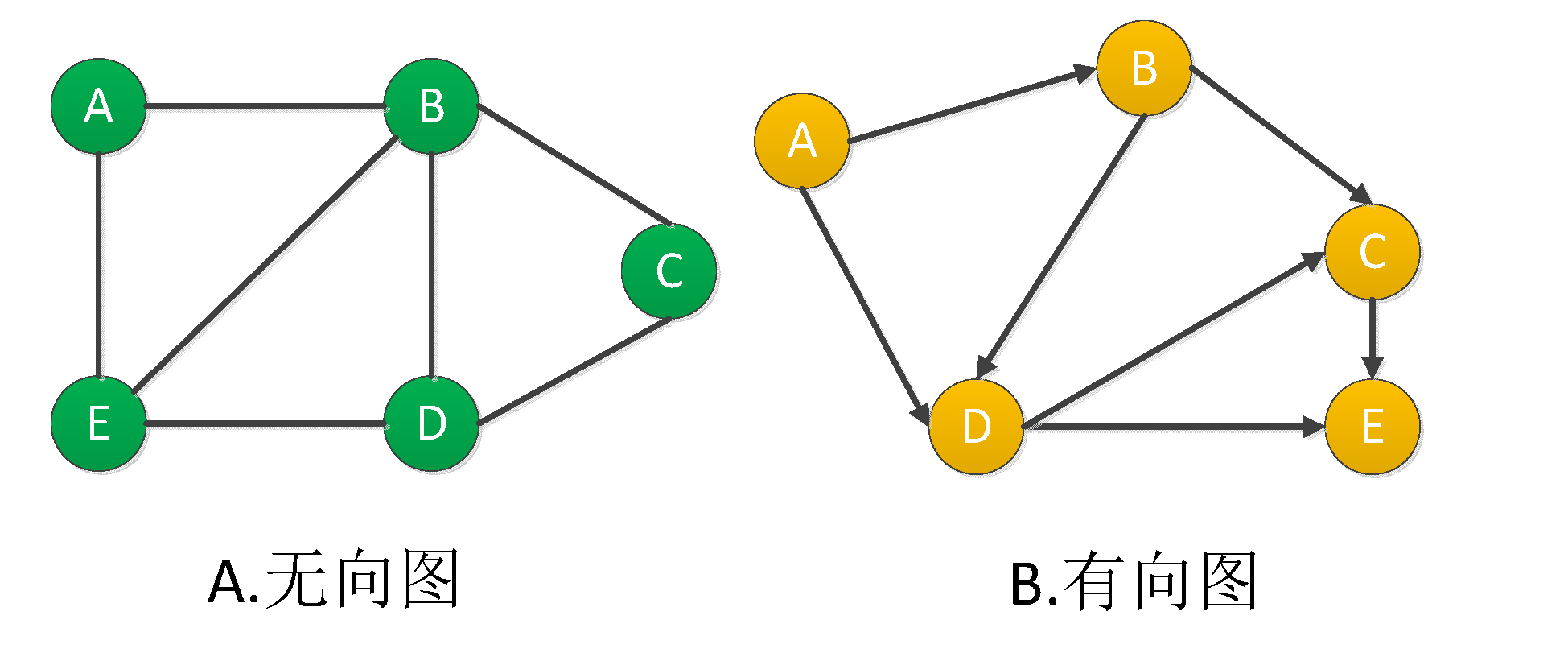
所谓的图G=(V,E)G=(V,E)，由顶点(Vertex) VV 和边(Edges) EE 组成。可以用两种标准方式来表示：

• 邻接链表
• 邻接矩阵

根据图是否有向，可以将图分为有向图和无向图。

邻接链表

邻接链表由 |V||V| 条链表构成，即每个顶点 Vi∈VVi∈V有一条链表，链表中存储该顶点的相邻顶点。一般来说，邻接链表更适合表示稀疏图(边的条数|E||E| 远远小于|V|2|V|2的图)。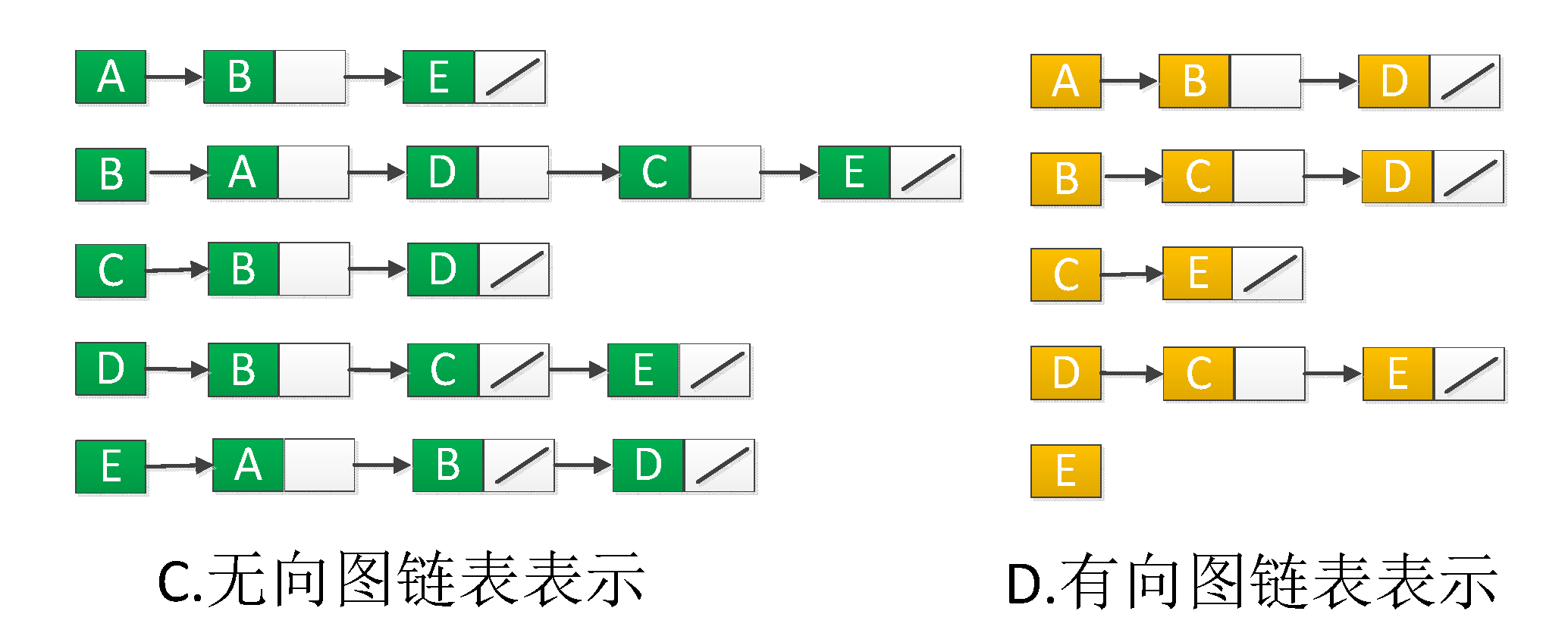

如上图所示，图C为无向图A(G=(V,E),|V|=5,|E|=7G=(V,E),|V|=5,|E|=7)的邻接链表表示，共有5条链表，且所有邻接链表的长度之和等于 2|E|2|E|, 即14。图D为有向图B(G=(V,E),|V|=5,|E|=7G=(V,E),|V|=5,|E|=7)得邻接链表表示，邻接链表的长度之和等于 2|E|2|E| 。不论是有向图还是无向图均需要的存储空间为 Θ(V+E)Θ(V+E)。

邻接矩阵

对于邻接链表而言，存在一个明显的不足就是无法快速判断边(u,v)(u,v) 是否为图中的边，而邻接矩阵恰恰克服了这一缺陷。
邻接矩阵，对于图GG而言，其邻接矩阵由 |V|×|V||V|×|V|的矩阵 A=(aij)A=(aij) 表示, 并满足以下关系:

• aij=1,如果(i,j)∈Eaij=1,如果(i,j)∈E
• aij=0,其他aij=0,其他

图E、图F分别给出了无向图与有向图的邻接矩阵表示，其空间需求皆为Θ(V2)Θ(V2)。与邻接链表相反，邻接矩阵更适合表示稠密图(边的条数|E||E| 接近 |V|2|V|2的图)。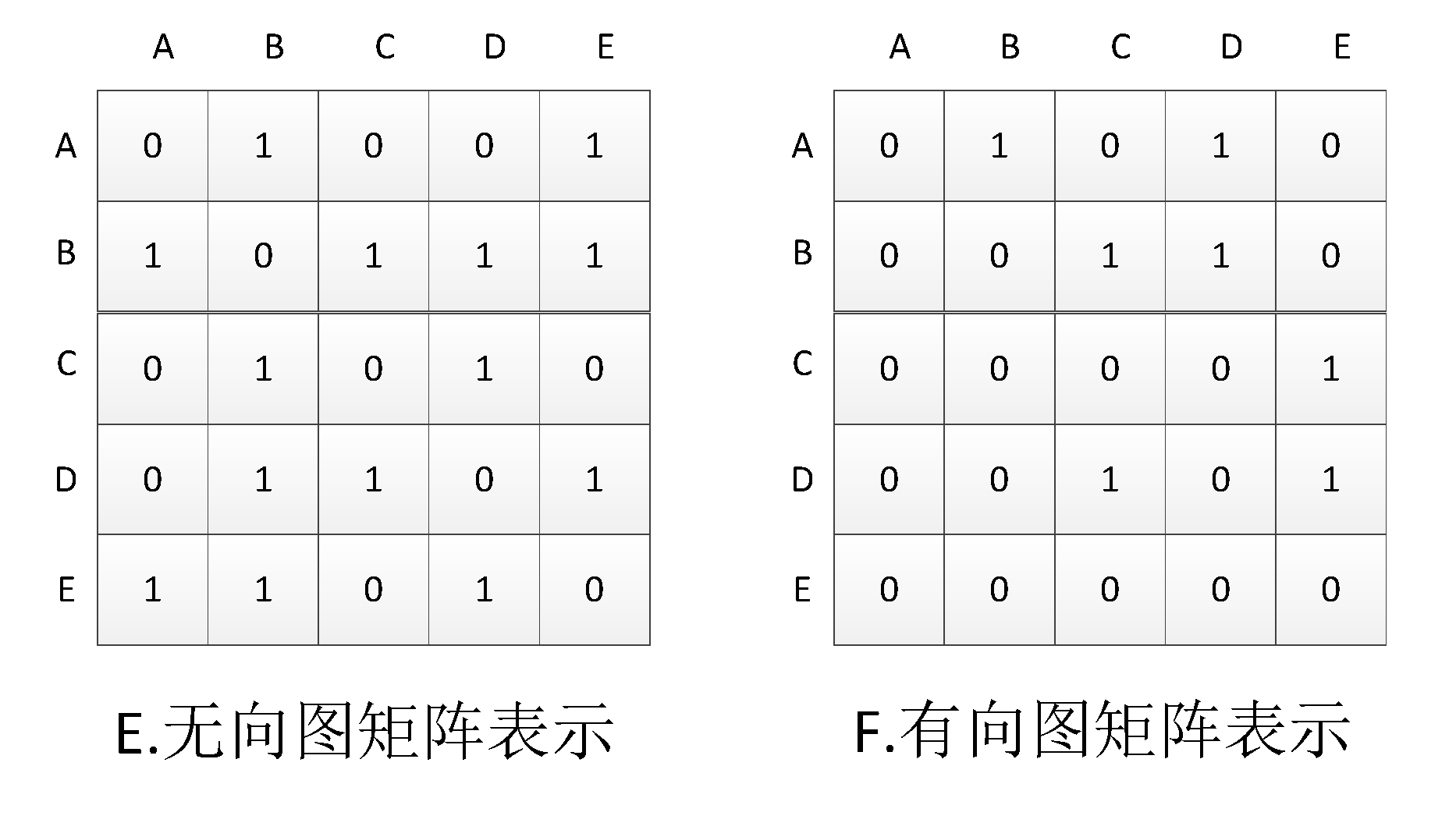

图的遍历

广度优先搜索(BFS)

给定图G=(V,E)G=(V,E)以及源点 SS, 通过调用广度优先算法可以发现从源点到达的所有顶点，同时生产一颗 “广度优先搜索树”。这里我们将借助一个先进先出(FIFO)的队列 QueueQueue 实现算法。
下面给出该算法的文字描述：

1. 初始化所有顶点，将顶点标记为未访问。
2. 将顶点 SS 存入队列 QueueQueue 中。
3. 如果队列 QueueQueue 非空，进入下一步，否则退出。
4. 出队列 DeQueueDeQueue ，得到顶点 uu，如果 uu 未被访问，进入下一步，否则回到步骤3。
5. 将 uu 标记为已访问，并将顶点 uu 的所有满足条件(1.未访问，2.队列中不存在该结点)的邻接结点存入QueueQueue 中,。
6. 打印顶点 uu，跳转到步骤3.

为了便于理解，我们结合图A中表示的无向图，源点为A，给出BFS的执行过程：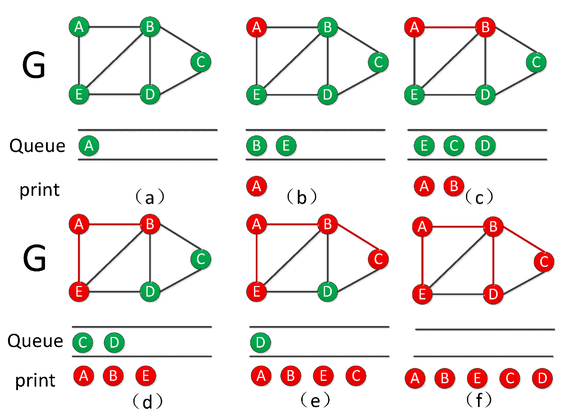

<1>. 如图(a)所示，我们初始化所有顶点状态未访问(用绿色表示)，将源点AA存入队列 QueueQueue。

<2>. 如图(b)所示，弹出AA并将其邻接结点B,EB,E加入队列中,输入AA。

<3>. 如图(c)所示，弹出队列头部元素BB，将其满足条件的邻接结点 C,DC,D 存入队列，输出 BB。

<4>. 如图(d)所示，弹出队列头部元素EE，其邻接结点均已入队列，输出 EE。

<5>. 如图(e)所示，弹出队列头部元素CC，其邻接结点均已入队列，输出 CC。

<5>. 如图(f)所示，弹出队列头部元素DD，其邻接结点均已入队列，输出 DD。

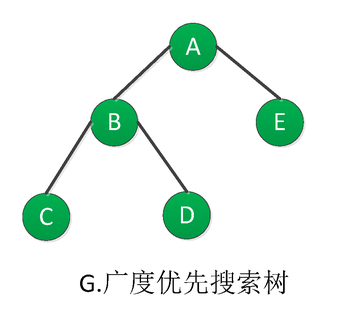
<6>. 队列 QueueQueue 为空，终止算法。最终得到输出数列 A,B,E,C,DA,B,E,C,D，其广度优先搜索树如下图G所示：

深度优先搜索(DFS)

深度优先搜索总是对最近才发现的结点 vv 的出发边遍历直到结点的所有出发边均被发现，然后再“回溯”到 vv 的前驱结点来搜索其出发边。这里我们借助栈 StackStack 的思想来描述算法。
下面给出该算法的文字描述：

1. 初始化所有顶点，将顶点标记为未访问。
2. 将出发点 SS 压入栈 StackStack 中。
3. 如果栈非空，进入下一步，否则退出结束算法。
4. 弹出栈顶结点 uu，如果 uu 未被访问，进入下一步，否则回到步骤3。
5. 将 uu 标记为已访问，并将顶点 uu 的所有满足条件(1.未访问，2.栈中不存在该结点)的邻接结点存入StackStack 中。
6. 打印结点 uu，跳转到步骤3.

为了更加直观的描述DFS的思路，我们结合图B 与源点 AA ，给出算法DFS的执行过程：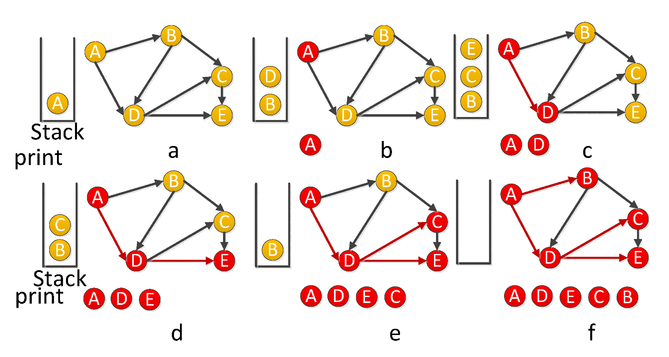

图的实现(Java)

邻接链表实现

图的邻接链表表示

我们知道描述一张图有两个最基本的元素结点 VV 和边 EE，在这里我们首先定义一个类Graph.java来表示图,将Vertex.java作为其内部类表示结点，实现代码如下。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

package com.pty.graph; import java.util.ArrayList; import java.util.LinkedHashMap; public class Graph<T> { private LinkedHashMap<T, Vertex> vertexs;// 使用LinkedHashMap存放图中的结点，结点标识T作为key能快速查找图中是否包含某结点 private LinkedHashMap<T, ArrayList<Vertex>> adjList; // 采用邻接链表的方式表示图，每个结点T对应于一个ArrayList链表，存放其相邻结点。 private int numOfVertex; // 图的结点数 private int numOfEdge; // 图的边数 private boolean directed; // 是否为有向图 public Graph(boolean directed) { vertexs = new LinkedHashMap<T, Vertex>(); numOfVertex = 0; adjList = new LinkedHashMap<T, ArrayList<Vertex>>(); this.directed = directed; } //省略相应的get、set方法 /** * 内部类，表示结点 * * @author john * */ public class Vertex { private T lable; // 标识结点，比如A0，A1，A2,...或者1，2，3，... private boolean visited; // 标识结点是否被访问 public Vertex(T tag, double score) { lable = tag; visited = false; } //省略相应的get、set方法 } }

 

图的基本操作

添加新的结点
每新增一个结点，将会创建一个ArrayList列表，用于存放新增结点的邻接结点。

1 2 3 4 5

public void insertVertex(T tag) { vertexs.put(tag, new Vertex(tag)); //新增结点 tag，如果定点中存在该结点将会被替换最新的 adjList.put(tag, new ArrayList<Vertex>()); //每新增一个结点，将会创建一个ArrayList列表，用于存放新增结点的邻接结点。 numOfVertex++; //结点数自增 }

 

添加新的边
这里暂时不考虑边的权值

1 2 3 4 5 6 7 8 9 10 11 12

public boolean addEdges(T start, T end) { if (vertexs.containsKey(start) && vertexs.containsKey(end)) { // 判断输入起始点是否合法 adjList.get(start).add(vertexs.get(end)); // 首先获取结点start的链表，然后将其邻接结点end加入其中 if (!directed) { //如果是无向图，则添加结束点到开始点的边 adjList.get(end).add(vertexs.get(start)); } } else { System.out.println("输入结点不合法"); return false; } return true; }

 

测试
打印图的链表结构

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

/** * 打印图的邻接链表 */ public void displayGraph() { System.out.println("邻接链表表示如下："); Iterator<Map.Entry<T, ArrayList<Vertex>>> iterator = adjList.entrySet().iterator(); while (iterator.hasNext()) { Map.Entry<T, ArrayList<Vertex>> element = iterator.next(); System.out.print(element.getKey() + ":"); displayList(element.getValue()); } } /** * 打印链表ArrayList * * @param list */ public void displayList(ArrayList<Vertex> list) { int size = list.size(); for (int i = 0; i < size; i++) { System.out.print(list.get(i).getLable()); if (i < size - 1) { System.out.print("-->"); } } System.out.println(); }

 

测试数据(无向图A)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

package com.pty.graph; public class Test { public static void main(String[] args) { Graph<String> graph = new Graph<String>(false); graph.insertVertex("A"); graph.insertVertex("B"); graph.insertVertex("C"); graph.insertVertex("D"); graph.insertVertex("E"); graph.addEdges("A", "B"); graph.addEdges("A", "E"); graph.addEdges("B", "C"); graph.addEdges("B", "D"); graph.addEdges("B", "E"); graph.addEdges("C", "D"); graph.addEdges("D", "E"); graph.displayGraph(); } }

 

控制台输出结果：
A:B–>E
B:A–>C–>D–>E
C:B–>D
D:B–>C–>E
E:A–>B–>D

图的相关算法

BFS实现

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

public void BFS(T start) { ArrayList<T> list = new ArrayList<T>(); // 存放遍历结点数列 LinkedList<Vertex> tempList = new LinkedList<Vertex>(); // 辅助BFS的队列 initialize(); //初始化所有结点访问属性为false tempList.add(vertexs.get(start)); while (!tempList.isEmpty()) { Vertex node = tempList.poll(); // 弹出队列头 if (!node.isVisited()) { node.setVisited(true); ArrayList<Vertex> neighbor = adjList.get(node.getLable()); // 获取结点node的邻接表 int size = neighbor.size(); for (int i = 0; i < size; i++) { if ((!neighbor.get(i).isVisited()) && (!tempList.contains(neighbor.get(i)))) { tempList.offer(neighbor.get(i)); // 将未被访问且不包含在辅助BFS队列中的结点存入队列 } } list.add(node.getLable()); } } /** * 输出遍历序列 */ System.out.print("广度优先："); int size = list.size(); for (int i = 0; i < size; i++) { System.out.print(list.get(i)); if (i < size - 1) { System.out.print("-->"); } } System.out.println(); }

控制台输出图A的 广度优先：A–>B–>E–>C–>D

DFS实现

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

public void DFS(T start) { ArrayList<T> list = new ArrayList<T>(); // 存放遍历结点数列 Stack<Vertex> stack = new Stack<Vertex>(); // 辅助DFS栈 initialize(); // 初始化所有结点访问属性为false stack.push(vertexs.get(start)); while (!stack.isEmpty()) { Vertex node = stack.pop(); //弹出栈顶元素 if (!node.isVisited()) { node.setVisited(true); ArrayList<Vertex> neighbor = adjList.get(node.getLable()); // 获取结点node的邻接表 int size = neighbor.size(); for (int i = 0; i < size; i++) { if ((!neighbor.get(i).isVisited()) && (!stack.contains(neighbor.get(i)))) // 将未被访问且不包含在辅助DFS栈中的结点压入栈 stack.push(neighbor.get(i)); } list.add(node.getLable()); } } System.out.print("深度优先："); int size = list.size(); for (int i = 0; i < size; i++) { System.out.print(list.get(i)); if (i < size - 1) { System.out.print("-->"); } } System.out.println(); }

控制台输出图A的 深度优先：A–>E–>D–>C–>B

附件

完整代码以及相应示例图见 https://github.com/lemon2013/algorithm

坚持原创技术分享，您的支持将鼓励我继续创作！

赏

• 本文作者： lemon
• 本文链接： https://lemon2013.github.io/2017/05/27/graph-search/
• 版权声明： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 3.0 许可协议。转载请注明出处！

转载于:https://my.oschina.net/u/1580214/blog/1377189