机器学习_2:K-近领算法
实验背景
本次实验基于机器学习经典的k-近邻算法,k-近邻算法的原理和基础的分类实验请参考我的上篇博客机器学习_1:K-近领算法,本次实验我们来解决如何用k近邻算法实现约会网站配对,和调试修改手写体识别的错误率。
1.约会网站配对
1.1实验背景

如图所示,本次实验属于分类实验,将每年获得的飞行常客里程数,玩视频游戏所耗时间百分比,以及每周消费的冰淇淋公升数作为输入变量,判断这个人是(讨厌,一般,喜欢)中的哪一类。
1.2算法解析
#从文本文件中解析数据
def file2matrix(filename):
fr = open(filename)
#获得文件内行数
numberOfLines = len(fr.readlines())
#返回值
returnMat = zeros((numberOfLines,3))
#标签列表
classLabelVector = []
fr = open(filename)
index = 0
for line in fr.readlines():
#截取所有回车字符
line = line.strip()
#使用tab字符将得到的整行数据分割成一个元素列表
listFromLine = line.split('\t')
#选取前三个元素存储到特征矩阵中
returnMat[index,:] = listFromLine[0:3]
#将列表最后一列存储到向量classLabelVector中
classLabelVector.append(int(listFromLine[-1]))
index += 1
return returnMat,classLabelVector
#归一化数据,将数字转化为0~1之间,公式newValue=(oldValue-min)/(max-min)
def autoNorm(dataSet):
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet))
m = dataSet.shape[0]
normDataSet = dataSet - tile(minVals, (m,1))
normDataSet = normDataSet/tile(ranges, (m,1))
return normDataSet, ranges, minVals
#分类器针对约会网站的测试代码,即训练模型
def datingClassTest():
hoRatio = 0.50
#读取文件数据
datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
#归一化数据
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
if (classifierResult != datingLabels[i]): errorCount += 1.0
print("the total error rate is: %f" % (errorCount/float(numTestVecs)))
print(errorCount)
#
def classifyPerson():
#类标签列表
resultlist=["讨厌","一般","喜欢"]
#用户输入不同特征值
precentTats = float(input("玩视频游戏所占时间百分比?"))
ffMiles = float(input("每年获得的飞行常客里程数?"))
iceCream = float(input("每周消费的冰淇淋公升数?"))
#打开文件并处理数据
datingDataMat,datingLabels = KNN.file2matrix('datingTestSet2.txt')
#归一化训练集
normMat, ranges, minVals = autoNorm(datingDataMat)
#创建测试集数组
inArr = np.array([precentTats, ffMiles, iceCream])
#归一化测试集
norm_in_arr = (inArr - minVals) / ranges
# 返回分类结果
classifierResult = classify0(norm_in_arr, normMat, datingLabels, 3)
#输出结果
print("你对这个人的感觉可能是: ", resultList[classifierResult - 1])
1.3算法实现
进入python后
import KNN
KNN.datingClassTest()
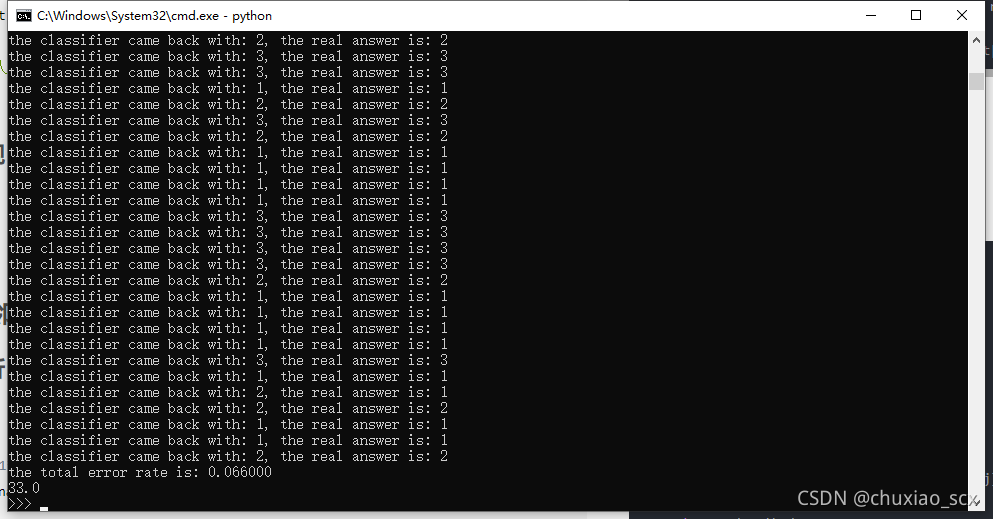
错误6.6%,有点高,让我们修改一下hoRatio的值,由0.5修改为0.1
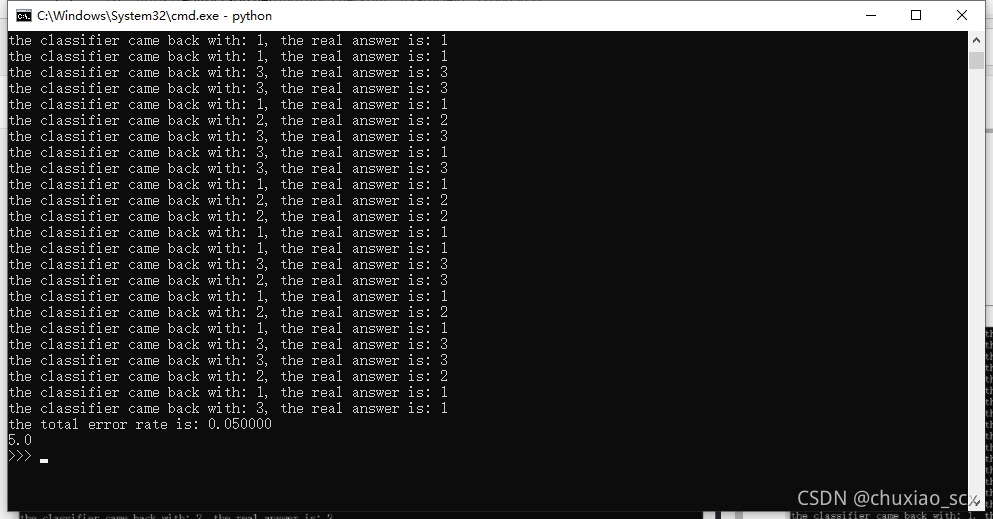
5%,还是有点高,修改下classify0中k的值
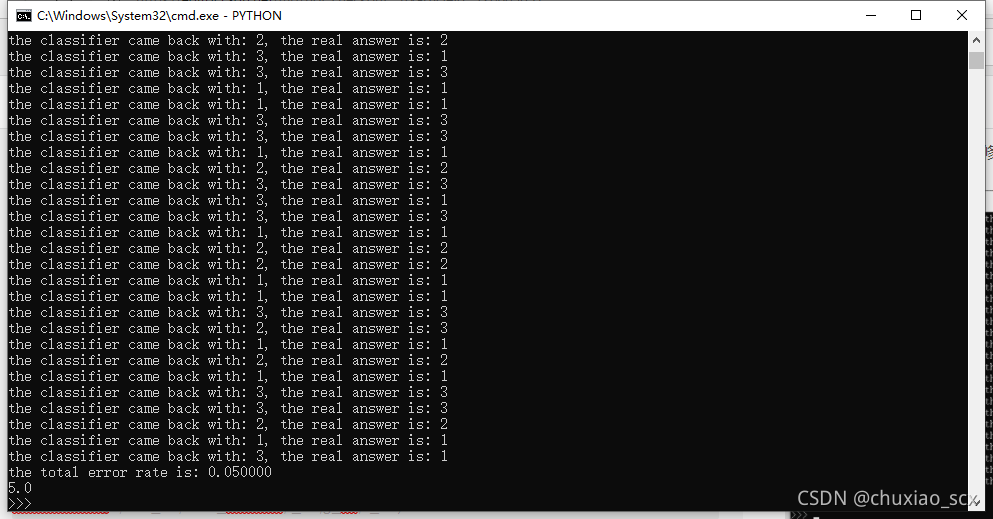
多次调试后发现不影响结果
再输入
KNN.classifyPerson()

输入信息进行判断
2.基于k-近邻算法的手写体识别
2.1参数修改,结果演示
将k值由3变为5
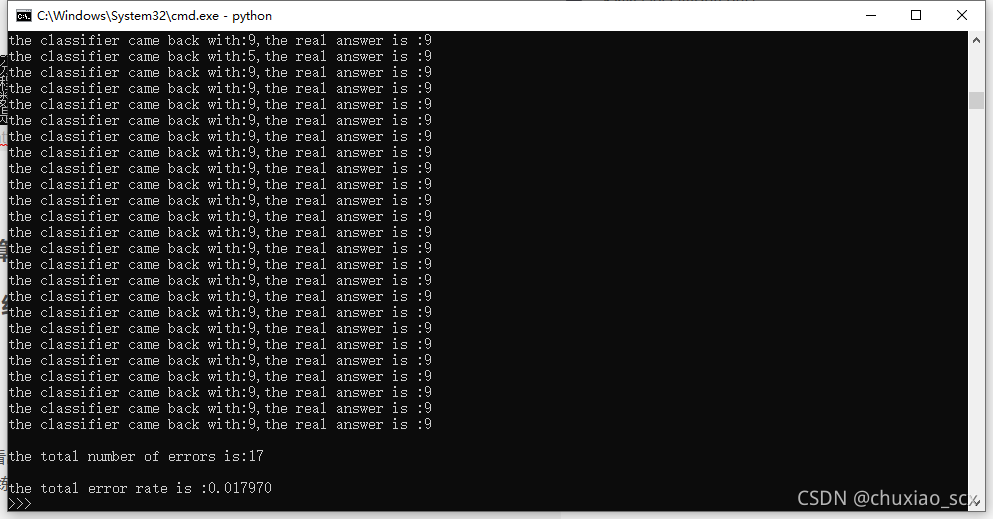
结果变差,错误率上升0.7%
将k变为1时
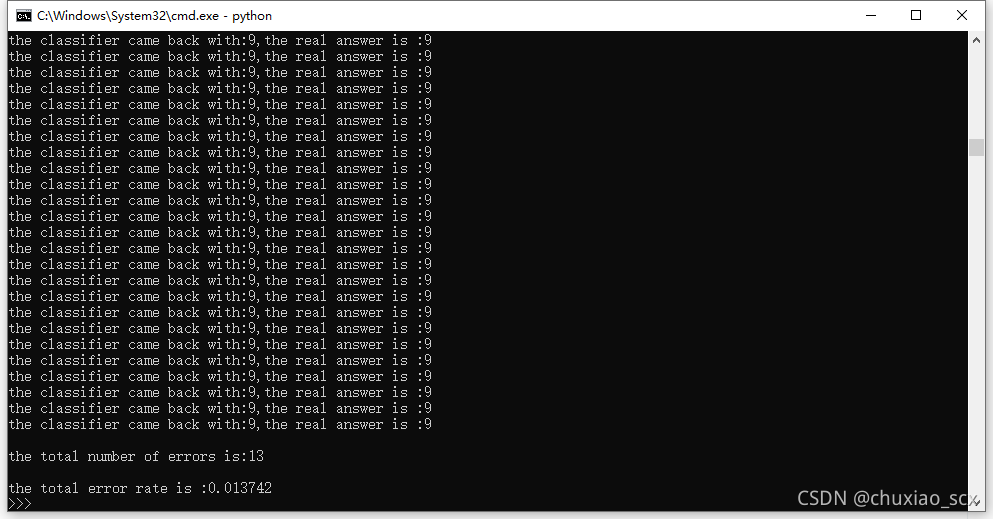
错误率还是比k为3时高
k值变为10时,错误率为2%
3.实验总结
本次实验可以进一步的看出K近邻算法的缺点
1.反复修改k值时重新训练所需时间过长
2.无法确认k值是否为最优
实验代码:github







 本文介绍了K-近邻算法在约会网站配对和手写体识别中的应用。通过实验,作者展示了如何利用算法处理数据,包括数据预处理和分类,并探讨了算法的优缺点。在约会网站匹配中,通过调整超参数,最终得到约6%的错误率。而在手写体识别上,调整k值影响了错误率,指出K近邻算法存在的问题,如参数选择的困难和训练时间较长。
本文介绍了K-近邻算法在约会网站配对和手写体识别中的应用。通过实验,作者展示了如何利用算法处理数据,包括数据预处理和分类,并探讨了算法的优缺点。在约会网站匹配中,通过调整超参数,最终得到约6%的错误率。而在手写体识别上,调整k值影响了错误率,指出K近邻算法存在的问题,如参数选择的困难和训练时间较长。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








