论文学习-一种基于相关性的分层预测方法，用于进化动态多目标优化

论文题目：A Correlation-Guided Layered Prediction Approach for Evolutionary Dynamic Multiobjective Optimization

一种基于相关性的分层预测方法，用于进化动态多目标优化（Kunjie Yu , Member, IEEE, Dezheng Zhang , Jing Liang , Senior Member, IEEE,KeChen , Member, IEEE, Caitong Yue , Member, IEEE, Kangjia Qiao , Member, IEEE, and Ling Wang , Member, IEEE）IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION, VOL. 27, NO. 5, OCTOBER 2023

刚开始学习多目标优化算法，不作商业用途，如果有不正确的地方请指正！

个人总结：

• 首先是针对LPM的出现问题提出一个解决办法,就是基于相关性分析得出每个个体前几方向和种群中心前进方向的相关性排序,把种群按照6:3:1的比例分成3个亚种群(高,中,低)相关性
• 针对高相关性的子群,采取LPM预测POS的运动方向
• 针对中相关性的子群,采取方向和长度矫正模型(DCM,LCM)自适应预测pos的变化
• 针对低相关性的子群,采取用之前保存的优异非支配解替代的策略来保持种群的多样性

摘要

• 现阶段,在利用进化算法求解动态多目标优化问题时,广泛采用pareto前沿的一些特殊点的历史运用方向,如中心点和拐点,来预测pareto最优解集.
• 但是某些特殊点可能会受到个别方向偏差大的个体影响,从而误导对动态pos的跟踪.
• 为了解决这个问题,作者提出基于相关性的分层预测方法，通过考虑个体运动方向的相关性，将多个预测模型融合在一起，求解DMOPs。
• 首先,通过相关性分析,将种群聚类为三个亚种群(高,中,低相关性),针对每个种群进行不同的预测行为.
• 高相关性的子群通过线性预测模型预测运动方向,中相关性的子群通过使用方向和长度矫正模型自适应预测pos的变化,低相关性的子群主要用来增加种群的多样性.

引言

在过去的十几年中,多目标优化算法因其高鲁棒性和广泛的适用性被用于处理各种静态MOPs.但是，DMOP 要求求解器在检测到变化时准确、快速地跟踪变化的帕累托最优解或帕累托最优前沿 。因此，将MOEA与动态响应策略相结合是处理DMOP的有效方法。

其中基于预测的方法显示出具有竞争力的性能，因为动态环境中的变化可能会表现出一些可预测的模式。尤其是,基于预测的方法设计整合了历史种群信息和先进的预测技术来估计后续种群，从而有效地跟踪不断变化的POS或POF.

种群划分的可行性

这一块讲述了种群划分的可行性,介绍了几个比较成功的种群划分算法.

两个关键任务

在动态环境变化中如何重新定位准确的POS位置,和跟踪不断变化的POS流形(manifold)

其中,具有不同移动方向的个体对解决这两个任务有不同的偏好,对于与其他个体移动方向差异较大的个体,可以用来跟踪不断变化的POS流行,而剩下的相同的个体可以再重新定位POS位置有良好的表现.

本文提出的想法

本文提出了一种基于相关性的分层预测（CGLP）DMOEA。通过相关性分析，得到个体与种群中心点之间的方向关联度，从而根据相关性程度的水平将个体形成不同的亚种群,每个亚种群被分配来处理不同的任务。并做出了如下贡献:

1. 通过测量个体的相关性，提出了一种种群划分策略。该策略可以估计重新定位 POS 位置和跟踪个人 POS 流形之间的优化偏好，从而将个体分配到不同的任务中。
2. 通过将更合适的个体分配到其预测过程来增强 LPM 的性能。通过在高关联层采用LPM，可以更准确地预测POS位置。
3. 提出了两种新模型[方向校正模型（DCM）和长度校正模型（LCM）]来跟踪POS流形。两种模型充分利用了个体的信息，大大提高了跟踪POS流形的能力。

背景及相关工作

A.DMOP基础

基础相关介绍,在这块略过.

B.相关分析

所谓相关分析,它是对动态过程发展趋势的定量比较分析,通过对系统各个维度相关统计数据的几何关系进行对比,几何形状的相似度越高，相关性就越高。通过相关性分析，可以计算出因子与系统之间的关联度.作者给出了如下定义:

1)Correlation Coefficient(相关系数):

由于系统中各种因素的含义不同，数据不便于直接比较，或者在比较过程中难以得到正确的结论。因此，相关性分析需要在计算相关系数之前对因子进行无量纲处理(dimensionless treatment)对于一个因子v使用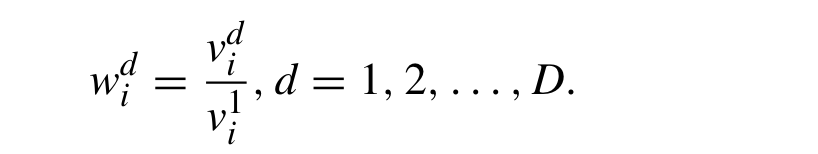计算出它的无量纲处理值w

在维度 d 中，比较因子 vi 与参考因子的相关系数可以通过下式计算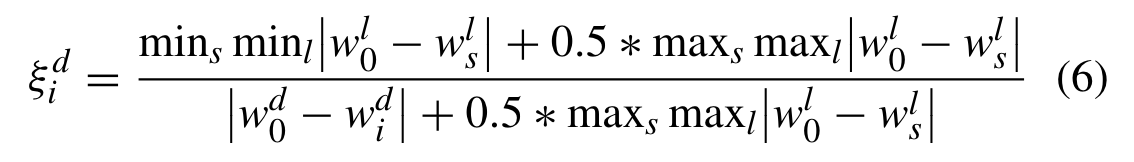其中w0是无量纲参考因子,ws是比较因子之一 ,msxs maxl分别是 W0 和 WS 的每个维度之间的最大和最小绝对差。

2)Correlation Degree(相关度)

相关系数衡量比较因子和参考因子在一个维度上的相关程度,因此各维度相关系数的平均值可作为比较因子与参考因子相关度的定量表达。相关度公式:相关度越大,参考因子和比较因子之间的相关性就越高.

C.线性预测模型

LPM是最常用的预测模型之一,它根据从先前环境中获取的步长和方向将解向量移动到新位置。通常，相邻环境非常相似，因此 LPM 会根据 POS 的最后移动方向转换当前人口。

优点:LPM只需要较少的相邻环境，早期历史信息的数量和质量不影响其预测性能。

假设Xot是种群Pt在t时刻的中心点,计算方式为:

再根据t-1时刻计算得出的X0t-1可以计算出中心点的移动方向V0

t+1时刻的预测就由如下公式产生: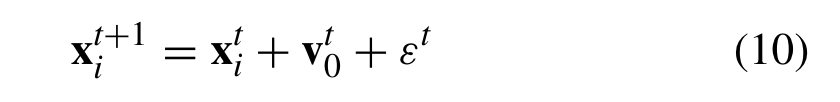

其中εt ∼ N(0, h) ,表示高斯噪声为0,标准差为h

LPM的算法为代码如下:

D.相关工作

这一块介绍了动态多目标优化算法的4种分类,并讲述了各个分类的一些优秀的算法

算法整体

A.动机

POS可以看作是两部分:POS位置,和它的流形. 而现有的预测策略中,LPM最常用来预测POS位置,在LPM中，中心点在最后一个环境中的移动方向将被视为POS的下一个移动方向.

LPM优点:只需要前面两个环境中的历史信息就可以预测下一个环境

LPM缺点:中心点的方向由种群中所有个体组成,如果某些个体的移动方向不同甚至冲突就会误导对POS位置的预测

为此作者认为可以找到具有相似移动方向的个体并结合这些多个方向来估计下一个POS位置,而那些与其他运动方向差异较大的个体更可能用来反映POS流形的变化.

所以采用了相关性分析,来估计个体之间的相关性

B.整体框架

整体的框架图如下:

首先,将进行种群重初始化，并通过静态 MOEA 对种群进行优化。然后，执行环境变化检测。如果发生环境变化，则进行CGLP过程以产生新的种群，否则，静态MOEA继续优化种群。

在 CGLP 中，根据相关性分析将总体分为三个水平，并设计了不同的策略来预测不同的水平.

SubPH由与中心点具有较高相关度的个体组成，SubPM由与中心点具有中等相关度的个体组成。其余具有低相关性的个体形成SubPL

• SubPH使用LPM预测出更准确的POS位置
• SubPM用于跟踪不断变化的POS流形
• 而SubPL中的个体被视为尚未收敛到POS或跟踪POS的效率低下,用之前环境获得的分布良好的非支配解代替它以保持种群的多样性

C.种群的划分

种群划分的伪代码如下:

 对于当前时间步长 xti 的个体，前一个时间步长 xt−1 i 中的相关解被标识为

xti 的移动方向 vti 如图所示： 

对于种群，个体的方向向量是比较因子，中心点的方向向量是参考因子。上面的相关系数和相关度公式用于计算个体与中心点之间的相关度。随后，根据相关程度对个体进行排序，并分为三个不同水平的亚群。

D.方向校正和长度校正模型

对于LPM来说,它总是关注特殊点,而忽略了其他个体能够反映POS流形变化的特征,所以在一些非线性变化的情况下,可能表现出较差的性能.

所以作者提出使用DCM(Direction Correction Model)来纠正每个个体的方向.

而对于向量来说,它由方向和长度组成,但在相关性分析中只考虑了向量的方向而忽略了长度,所以对于个体来说即使他们具有高度相关的方向,但是在长度上也可能有很大差异.

为了解决这个问题作者提出使用LCM(Length Correciton Model)来用于矫正向量的长度

伪代码如下:

DCM例子展示

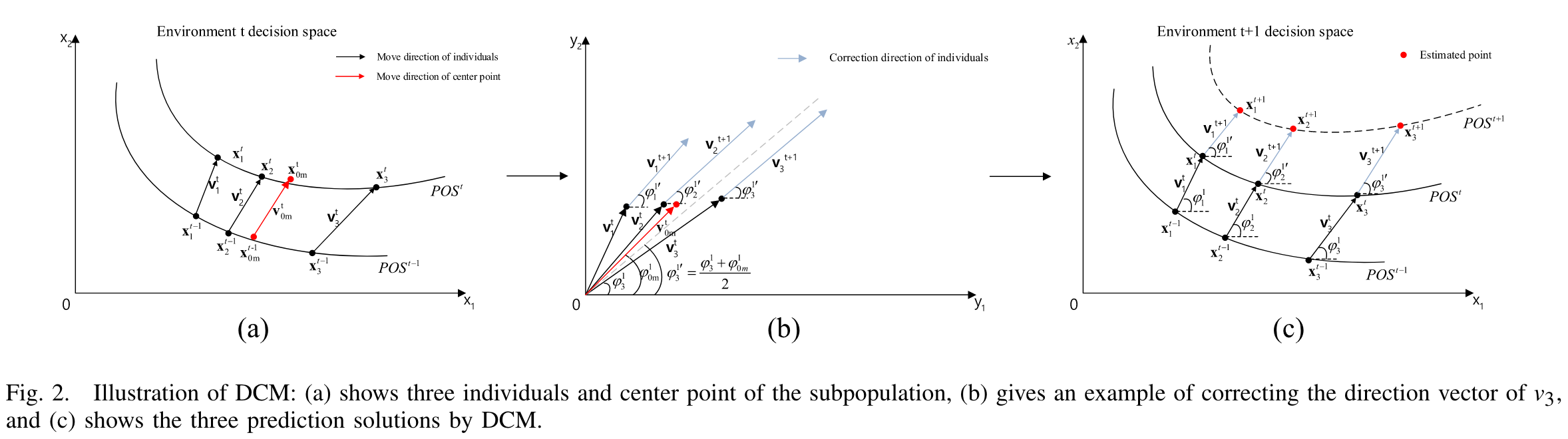
首先,根据前面给的公式,计算出SubPM中个体X1,X2,X3中心点X1和他们的方向向量V1,V2,V3,V0

其次,转换到球面坐标系,把向量vi=(vi1,vi2,-,vid)转换成vi=(ψi1,ψi2,-,ψiD-1,|vi|),其中ψij(1≤j≤D-1)是角坐标,|vi|是向量长度.,在用如下公式把角坐标Vi转换成直角坐标

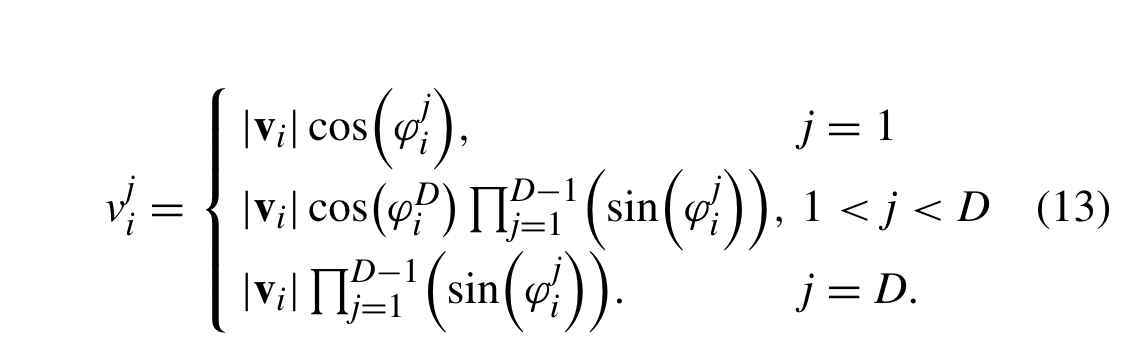
也可通过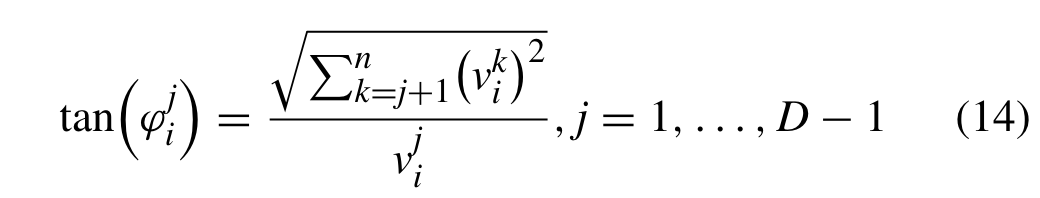把直角坐标转换成角坐标 

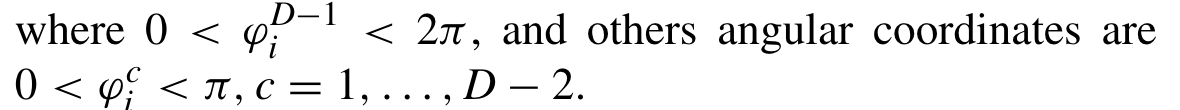第三步通过中心点和个体的移动来混合预测角度。预测角度的公式如下

最后再将预测向量从标准球面坐标系转换为直角坐标系 

LCM

DCM倾向于单一的个体信息，而LPM则侧重于整个人群的信息,然而，单个个体的运动方向并不稳定。因此，受LPM的启发，提出了LCM。与LPM不同，LCM中方向向量的长度被单个个体的长度所取代。 公式如图:

自适应调整策略

DCM和LCM组成预测出SubPt+1 M，但是需要有效的管理使用这两个模型,所以作者提出了一个自适应调整策略.

根据两个模型在前一个环境中的性能动态调整两个模型的选择概率,伪代码如图所示:

 对于一开始的两个环境,概率都设置为0.5.在往后的环境中,把两个模型生成的个体保存在外部存档中,一旦检测到环境变化，就会使用一个指标，即每个预测解与MOEA最近优化解的距离的平均值，来衡量哪个模型更好。指标定义如下：

SetT是时间 t 中大小为 Ns 的预测个体的集合,PtR为MOEA在时间t内优化的种群.

在算法中对两个模型的dis值进行比较.较低的值表示它所属的集合更准确，因此该模型的选择概率更高。

E.变化监测

作者在这块采用随机选择5%的个体作为检测器，检测器的值保存在档案中。在静态MOEA演化之前，再次计算检测器，判断目标值是否发生变化。一旦存储的目标值和重新评估的目标值之间存在差异，则认为发生了新的变化，并采用预测策略CGLP来跟踪下一个POS。 否则，静态MOEA将继续进化种群。 

F.复杂度的计算

实验研究

the proportion of individuals in SubPH, SubPM, and SubPL is 6:3:1

准备复现的时候再看