手撕 AVL 树 C 代码

一、调整不平衡的 AVL 树（左旋 & 右旋）

注意

调整前，首先要学会找到最小失衡子树，参见下例

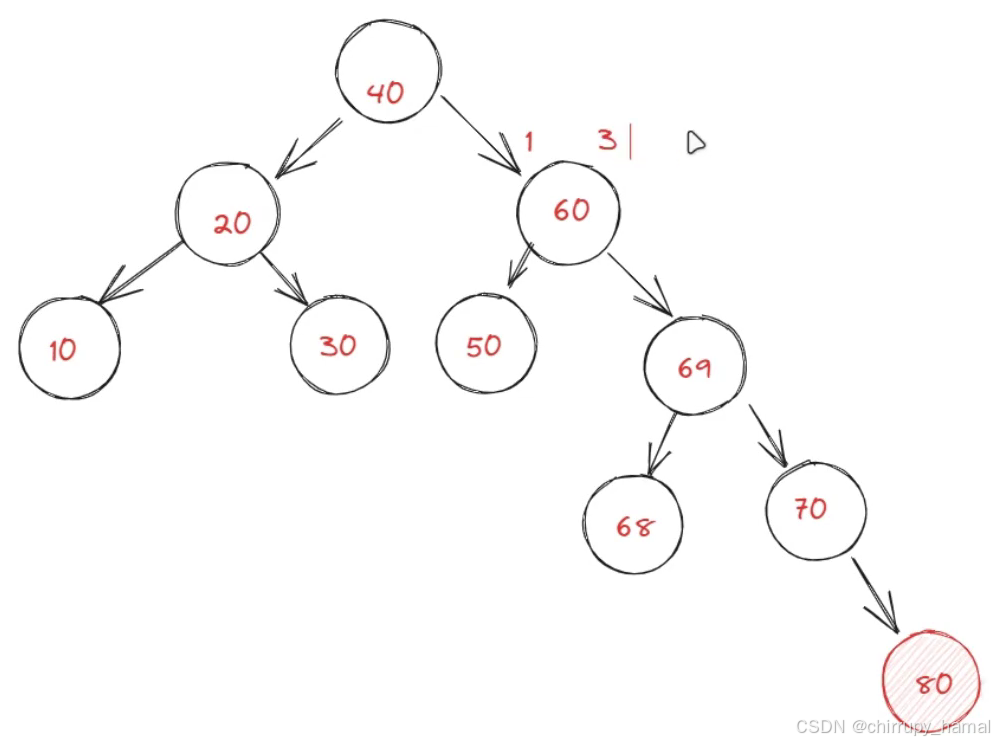
新插入的节点：80

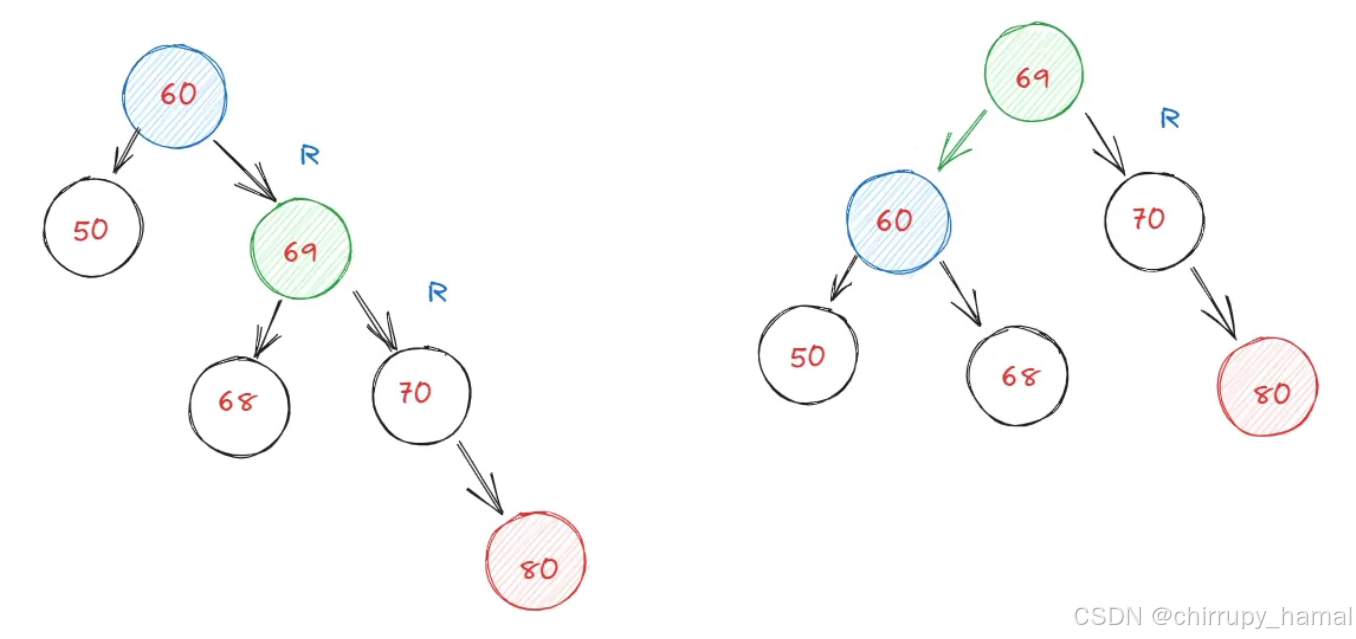
二、失衡情况

1、插入

1.1、LL 型失衡

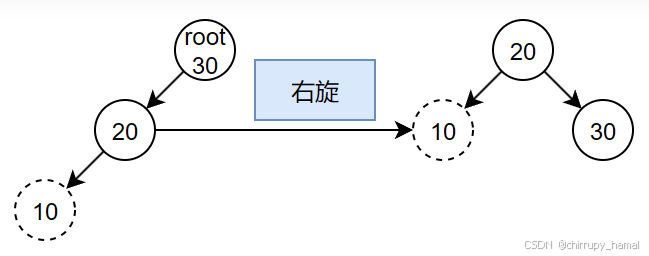
新插入的节点：10
失衡位置：root 左孩子节点的左子树上
平衡方法：右旋

1.2、LR 型失衡

新插入的节点：25
失衡位置： root 左孩子节点的右子树上
平衡方法：

1. 左旋 root 左子树
2. 右旋

1.3、RR 型失衡

失衡位置：root 右孩子节点的右子树上
平衡方法：左旋

1.4、RL 型失衡

失衡位置：root 右孩子节点的左子树上
平衡方法：

1. 右旋 root 右子树
2. 左旋

2、删除（LL、LR、RR & RL）

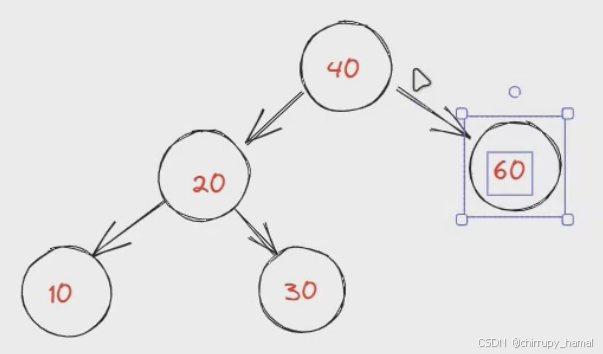
删除节点：60

1. 先找到最小失衡子树
   
2. 平衡方法：右旋（参见章节一中的右旋示例图）

二、代码实现

#include <stdio.h>
#include <stdlib.h>

typedef struct Node
{
  int val;     /* 数据域 */
  int height;  /* 树高 */
  struct Node *left;
  struct Node *right;
} Node;

Node *newNode(int val)
{
    Node *node = (Node *)malloc(sizeof(Node));
    node->val = val;
    node->height = 1;
    node->left = NULL;
    node->right = NULL;

    return node;
}

/* 获取树高 */
int getHeight(Node *node) 
{
  /* 空树 */
  if (!node)
    return 0;
   
  return node->height;
}

int max(int a, int b) 
{
  return (a > b) ? a : b;
}

/*
 * 1、原根节点的右孩子节点作为新树的根节点
 * 2、原根节点会作为新树根节点的左孩子节点
 * 3、如果新根节点原来有左子树，那么就作为旧根节点的右子树
 */
Node *leftRoate(Node *root)
{
  /* 1、原根节点的右孩子节点作为新树的根节点 */
  Node *newroot = root->right;
  /* T2 用来保存新树根原来的左子树 */
  Node *T2 = newroot->left;

  /* 2、原根节点会作为新树根节点的左孩子节点 */
  newroot->left = root;
  /* 3、如果新根节点原来有左子树，那么就作为旧根节点的右子树 */
  root->right = T2;

  /* 更新树高，root newroot */
  root->height = 1 + max(getHeight(root->left), getHeight(root->right));
  newroot->height = 1 + max(getHeight(newroot->left), getHeight(newroot->right));

  return newroot;
}

/* 右旋 */
Node *rightRotate(Node *root)
{
  Node *newroot = root->left;
  Node *T2 = newroot->right;

  newroot->right = root;
  root->left = T2;

  root->height = 1 + max(getHeight(root->left), getHeight(root->right));
  newroot->height = 1 + max(getHeight(newroot->left), getHeight(newroot->right));

  return newroot;
}

/* 获取平衡因子 */
int getBalance(Node *node) 
{
  return getHeight(node->left) - getHeight(node->right);
}

Node *insertNode(Node *node, int key)
{
  if (node == NULL)
    return newNode(key);

  if (key < node->val)
    node->left = insertNode(node->left, key);
  else if (key > node->val)
    node->right = insertNode(node->right, key);
  else
    return node;
    
  /* 更新树高 */
  node->height = 1 + max(getHeight(node->left), getHeight(node->right));

  /* 获取当前节点的平衡因子 */
  int balance = getBalance(node);
  /* LL 型失衡 */
  if (balance > 1 && getBalance(node->left) > 0)
    return rightRotate(node);

  /* LR 型失衡 */
  if (balance > 1 && getBalance(node->left) < 0) 
  {
    node->left = leftRoate(node->left);
    return rightRotate(node);
  }

  /* RR 型失衡 */
  if (balance < -1 && getBalance(node->right) < 0)
    return leftRoate(node);

  /* RL 型失衡 */
  if (balance < -1 && getBalance(node->right) > 0)
  {
    node->right = rightRotate(node->right);
    return leftRoate(node);
  }

  return node;
}

Node *deleteNode(Node *node, int key) 
{
  Node *temp;
  int   balance;
  
  if (node == NULL)
    return node;

  if (key < node->key)
    node->left = deleteNode(node->left, key);
  else if (key > node->key)
    node->right = deleteNode(node->right, key);
  else 
  {
    if (NULL == node->left && NULL == node->right) 
    {
      temp = node;
      node = NULL;
      free(temp);
    }
    else if (NULL == node->left && NULL != node->right)
    {
      temp = node;
      node = node->right;
      free(temp);
    }
    else if (NULL != root->left && NULL == root->right)
    {
      temp = node;
      node = node->left;
      free(temp);
    }
    else
    {
      Node *cur = node->right;
	
      while (cur->left)
        cur = cur->left;

      node->val = cur->val;
      node->right = deleteNode(node->right, cur->val);
    }
  }

  if (node == NULL)
    return node;

  node->height = 1 + max(getHeight(node->left), getHeight(node->right));

  balance = getBalance(node);
  /* LL 型失衡 */ 
  if (balance > 1 && getBalance(node->left) >= 0)
    return rightRotate(node);

  /* RR 型失衡 */
  if (balance < -1 && getBalance(node->right) <= 0)
    return leftRotate(node);

  /*
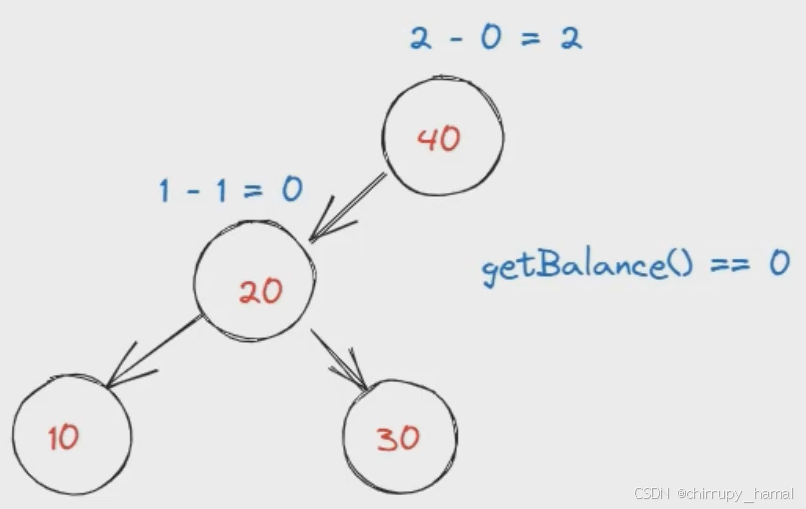
   * LL 和 RR 型失衡相较 insertNode() 的 LL 和 RR 有所不同
   * 会多出 getBalance(node->left) == 0 和 getBalance(node->right) == 0 的情况
   * 以 getBalance(node->left) == 0，也就是右旋为例，具体可参见章节二中 2 小节的示例图
   */

  /* LR 型失衡 */
  if (balance > 1 && getBalance(node->left) < 0) 
  {
    node->left = leftRotate(node->left);
    return rightRotate(node);
  }

  /* RL型失衡 */
  if (balance < -1 && getBalance(node->node) > 0) 
  {
    node->right = rightRotate(node->right);
    return leftRotate(node);
  }

  return node;
}

/* 先序遍历 */
void preOrder(Node *root)
{
  if (!root)
    return;
    
  printf("%d ", root->val);
  preOrder(root->left);
  preOrder(root->right);
}

/* 中序遍历 */
void midOrder(Node *root) 
{
  if (!root)
    return ;
    
   midOrder(root->left);
   printf("%d ", root->val);
   midOrder(root->right);
}

Node *find(Node *root, int key, int *counter)
{
  Node *cur = root;
  while (cur != NULL)
  {
    if (key < cur->val)
    {
      cur = cur->left;
      (*counter)++;
    }
    else if (key > cur->val) 
    {
      cur = cur->right;
      (*counter)++;
    }
    else
      return cur;
  }
    
  return NULL;
}

void test() 
{
  Node *root = NULL;

  root = insertNode(root, 10);
  root = insertNode(root, 20);
  root = insertNode(root, 30);
  root = insertNode(root, 40);
  root = insertNode(root, 50);
  root = insertNode(root, 60);
  root = insertNode(root, 70);

  int counter = 0;
  Node *result = find(root, 70, &counter);
  printf("找了几次: %d\n", counter);
  printf("-------先序遍历结果--------\n");
  preOrder(root);
  printf("\n-------中序遍历结果--------\n");
  midOrder(root);
  printf("\n");

  counter = 0;
  root = deleteNpde(root, 10);
  root = deleteNpde(root, 20);
  root = deleteNpde(root, 30);
  result = find(root, 40, &counter);
  printf("找了几次: %d\n", counter);
  printf("-------先序遍历结果--------\n");
  preOrder(root);
  printf("\n-------中序遍历结果--------\n");
  midOrder(root);
  printf("\n");
}

int main()
{
  test();
  return 0;
}