二叉搜索树详解

一、二叉搜索树概念

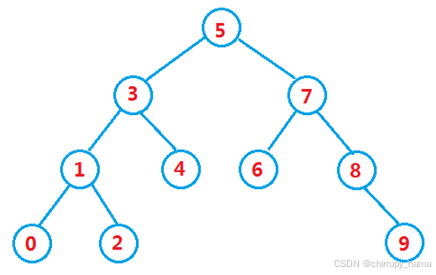
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也是二叉搜索树

二、二叉搜索树操作

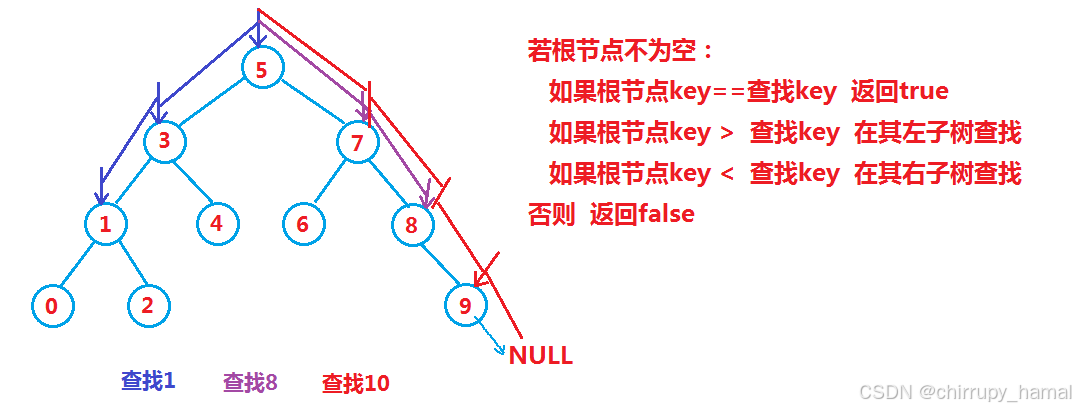
1、查找

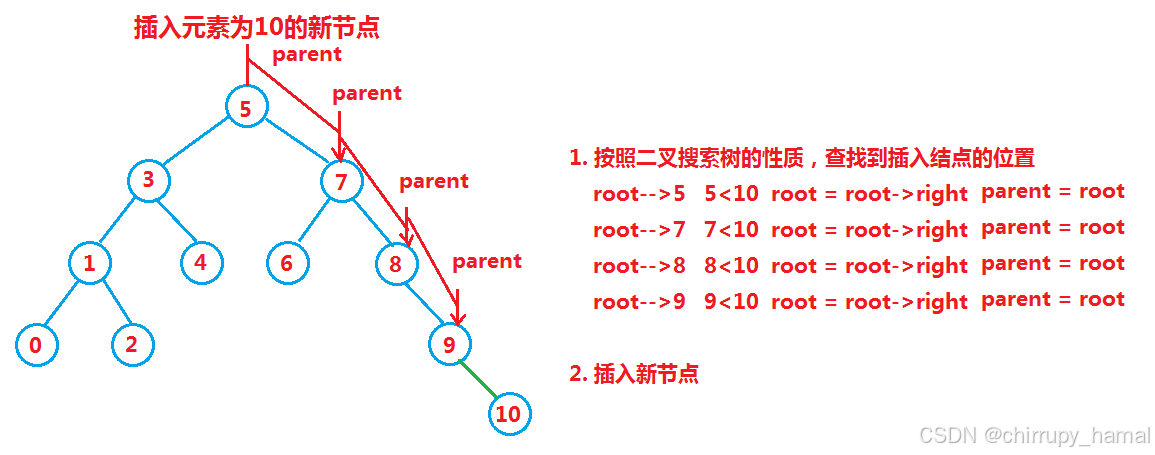
2、插入

先查找，若不存在，则插入

• 空树
  
• 非空树
  

3、删除

先查找，若存在，则删除

• 要删除的节点无孩子节点
  • 直接删除该节点
• 要删除的节点只有左孩子节点
  • 使该节点的父节点指向该节点的左孩子节点，然后删除该节点
• 要删除的节点只有右孩子节点
  • 使该节点的父节点指向该节点的右孩子节点，然后删除该节点
• 要删除的结点有左、右孩子节点
  • 将其右子树中序下的第一个节点值(最小值)填入待删除节点，最后删除 “最小值” 节点
  • 或者将其左子树中序下的最后一个节点值(最大值)填入待删除节点，最后删除 “最大值” 节点

三、二叉搜索树性能

插入或删除前必须先查找，也就是说，查找效率代表了二叉搜索树中各操作性能

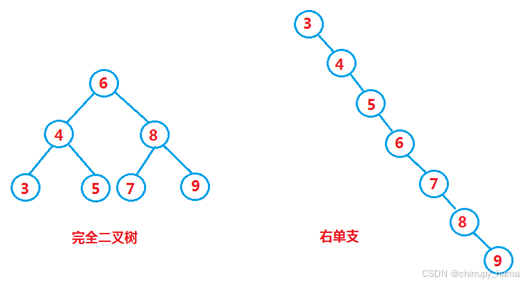
• 最优情况下，时间复杂度为 O(log₂N)
  • 二叉搜索树为完全二叉树，int a[ ] = {6, 4, 8, 3, 5, 7, 9};
• 最差情况下，时间复杂度为 O(N)
  • 二叉搜索树退化成单支树，int a[ ] = {3, 4, 5, 6, 7, 8, 9};

引申问题

如何避免二叉搜索树退化成单支树？
答：平衡二叉搜索树