机器学习算法——lasso

最新推荐文章于 2025-02-27 22:23:10 发布

CVlab-swin

最新推荐文章于 2025-02-27 22:23:10 发布

阅读量1.5k

点赞数

本文介绍了Lasso回归及前向逐步回归两种特征选择方法，并通过Matlab实现了前向逐步回归算法，最后展示了权重参数随迭代次数变化的收敛曲线。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、lasso

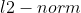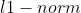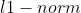前面已经叙述了基本的线性回归，局部加权线性回归，以及岭回归。其中，局部加权线性回归做的工作就是进行了特征的选择，选择的策略是进行局部的约束；岭回归是采用的正则化的方法进行特征的选择，使用的是 $l2-norm$ 。而lasso采用的则是 $l1-norm$ ，即lasso是在平方误差的基础上增加 $l1-norm$ ：

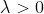
$\sum_{i=1}^{n}\left ( y_i-\sum_{j=0}^{p}w_jx_{ij} \right )^2+\lambda \sum_{j=0}^{p}\left | w_j \right |$ ， $\lambda> 0$

对于这样的一种优化问题，其实是很难求解的，因为这样的优化问题不再是一个凸优化问题。为了求解这样的问题，一些近似的优化算法被采用。或者可以采用一些简单的方法来近似这样的优化过程。

二、前向逐步回归

前向逐步回归算法可以得到与lasso差不多的效果，但是前向逐步回归更加简单。这是一种贪心算法，在每一步尽量减少误差。

(前向逐步回归流程)

三、实验

1、Matlab实现

主程序

[plain]view plaincopy 
    
 clear all;  
 clc;  
 %% 导入数据  
 data = load('abalone.txt');  
 x = data(:,1:8);  
 y = data(:,9);  
 %% 处理数据  
 yMean = mean(y);  
 yDeal = y-yMean;  
 xMean = mean(x);  
 xVar = var(x,1);  
 [m,n] = size(x);  
 xDeal = zeros(m,n);  
 for i = 1:m  
     for j = 1:n  
         xDeal(i,j) = (x(i,j)-xMean(j))/xVar(j);  
     end  
 end  
   
 %% 训练  
 runtime  = 5000;%迭代的步数  
 eps = 0.001;%调整步长  
 wResult = stageWise(xDeal, yDeal, eps, runtime);  
   
 %% 根据wResult画出收敛曲线  
 hold on   
 xAxis = 1:runtime;  
 for i = 1:n  
     plot(xAxis, wResult(:,i));  
 end  

前向逐步回归函数

[plain]view plaincopy 
    
 function [ wResult ] = stageWise( x, y, eps, runtime)  
     [m,n] = size(x);%数据集的大小  
     wResult = zeros(runtime, n);%最终的结果  
     w = zeros(n,1);  
     wMax = zeros(n,1);  
     for i = 1:runtime  
         ws = w'%输出每一次计算出来的权重  
         lowestError = inf;%定义最小值  
         for j = 1:n  
             for sign = -1:2:1  
                 wTest = w;%初始化  
                 wTest(j) = wTest(j)+eps*sign;%只改变一维变量  
                 yTest = x*wTest;  
                 %求误差  
                 rssE = rssError(y, yTest);  
                 if rssE < lowestError%如果好，就替换  
                     lowestError = rssE;  
                     wMax = wTest;  
                 end  
             end  
         end  
         w = wMax;  
         wResult(i,:) = w;  
     end  
 end  

误差函数

[plain]view plaincopy 
    
 %% rssError函数主要是利用均方误差  
 function [ error ] = rssError( y, yTest )  
     yDis = y-yTest;%误差  
     [m,n] = size(yDis);  
     %求平方  
     for i = 1:m  
         yDis(i) = yDis(i)^2;  
     end  
     error = sum(yDis);%求列和  
 end  