为什么浮点数不能直接比较大小

最新推荐文章于 2025-03-08 10:23:15 发布
原创 最新推荐文章于 2025-03-08 10:23:15 发布 · 5.8k 阅读 · 6 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文解析了浮点数在计算机中的表示方式及其对运算的影响，揭示了为什么看似简单的数学等式在计算机中可能不成立的原因，同时探讨了0.1+0.5==0.6为何在计算机中为真的原理。

以JS为例
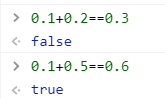
在这里插入图片描述
在这里插入图片描述
简短的解释就是，浮点数在计算机中大部分都是近似
0.1 可以表示为
0.000110011001100110011001100110011001100110011001100110…
其后是一个无限循环的小数，计算机只能截断，很显然截断后的数就已经是0.1的近似值了，但是两个0.1的在计算机的表示是一致的，所以0.1==0.1是成立的
在这里插入图片描述
而经过计算后的浮点数，是两个近似值计算得到值，计算机不能把他识别为是1位小数0.3而是0.3000…4，与真计算值的表示方式很可能是不相同的，所以他们不等。

再来解释为什么0.1+0.5==0.6是true

因为0.5在计算机是可以准确表示为0.1000000000的，那么一个被截断的数和他相加后得到的虽然也是一个近似值，但是0.1小数第一位后面的0和1，在0.1+0.5计算中是没有变过的，他们的表示方式和0.6小数第一位后面的0和1是相同的

所以即使这是一个0.6的近似数，比较结果是true

我还有一个疑问是，计算机如何把0.0001100110011001…输出的时候转换为0.1？

aaaaa2134
关注
浮点数的陷阱：你以为的 0.1 + 0.2其实不是 0.3，BigDecimal你真的用对了吗？
曾经“等你生日那天”都遥远得像未来，如今却可欢愉的挥手说“下个十年见”
05-18 13万+
在金融和交易系统中，哪怕是一分钱的误差都可能造成巨大损失。然而，很多开发者仍在不经意间落入浮点数的陷阱：看似简单的 0.1 + 0.2，为什么在 Java 中不等于 0.3？本篇文章从底层的 IEEE 754 浮点数标准讲起，剖析误差来源，逐层构建 BigDecimal 使用、格式化控制、精度舍入、判等策略等防线，并结合真实案例总结出一套浮点数处理的实战规范，助你规避金额计算中的隐性风险。
浮点数不能进行相等性运算的原因
小红九さんの技術ブログ
09-26 3298
只能尝尝味道，离吃饱差的远
为什么两个不确定值的浮点数无法直接比较是否相等
河 的 第 三 条 岸
06-07 5568
C语言贴吧看到的： 首先，为了让代码清楚一点，把楼主耍小聪明的伎俩去掉： 程序运行的结果是执行了if (a != a) 语句块的内容。 a = a / a 没什么好奇怪的，关于执行的结果我开始是这么认为的： a = a / a 完了之后a 的值是NaN，表示不是任何数（后来我发现，对于大多数环境来说，这个没有定死）。 NaN 的32 位精度储存是这样的：
浮点型数据不能直接比较
G4fun's Blogs
05-12 398
浮点型数据不能直接比较 将float==0的判断条件根据精准度改变,如保留一位小数,改成float>-0.05&&float<0.05 编程题: 计算2个复数的和、差、积、商。 输入格式： 输入在一行中按照a1 b1 a2 b2的格式给出2个复数C1=a1+b1i和C2=a2+b2i的实部和虚部。题目保证C2不为0。 输出格式： 分别在4行中按照(a1+b1i) 运算符 (a2+b2i) = 结果的格式顺序输出2个复数的和、差、积、商，数字精确到小数点后1位。如果结果的实部
浮点数的大小比较
热门推荐
超空间
05-28 1万+
浮点数在转换过程中都会有误差的,所以浮点数不能直接比较其大小,一般在比较两个浮点数的时候是比较他们之间的差值,如果两个数之间的差值处于一个能接受的范围之内的话,那么,我们就认为这两个浮点数是相等的,一般认为A与B的差大于某个很小的数时就认为A>B，比如:if( A-B > 0.001 ){ A>B...   }一般来说这个可以接受的误差值就是计算机的转换误差,C++标准库提供了这个误差,你可以
为什么float类型数据不能直接比大小
mh_dream的博客
10-20 3664
float类型数据不能直接比大小，需要做一些处理才行，这是由计算机采用二进制的方式存储数据导致的。 十进制整数转二进制： 十进制数除2，取余，从最后一个余数到第一个余数得到的数，即为转换后得到的二进制值。 13的二进制为1101 十进制小数转二进制： 小数部分乘以2，取整数部分，从第一个到最后一个整数，得到的数，即为小数部分的二进制值。但是小数部分可能会出现无限循环的情况，所以float...
python中如何正确进行浮点数的大小比较
tzzqn2008的专栏
03-08 1183
请不要轻易直接比较浮点数的大小，因为这可能会出现非预期的结果。
Golang中精确比较浮点数大小的实用方法
07-01
资源下载链接为： ...浮点数在计算机中以二进制存储时，无法精确表示十进制小数（如0.1），导致运算和比较存在固有...避免直接比较浮点数相等性 这种误差是计算机底层表示机制决定的，非编程语言缺陷，需开发者主动规避。
浮点数原码补码反码比较大小
07-01
2.讨论原码、反码、补码在整数上下文，然后解释为什么浮点数不同。 3.如何比较浮点数的大小：在IEEE754中，浮点数的大小比较可以通过比较它们的二进制表示来实现，但由于指数偏置，正数和负数的比较是直接的。 比较...
精选资源
TIA博途-32位浮点数大小端存储-高低字节转换的具体方法示例（4种字节排列顺序）.docx
05-25
在计算机科学中，32位浮点数...总之，理解和掌握浮点数的大小端存储以及高低字节转换在TIA博途中是至关重要的，特别是在进行跨平台或网络通信的程序设计时。通过这个FB块的示例，我们可以更直观地学习并应用这些概念。
关于浮点数不能进行比较的问题
weixin_46217643的博客
03-09 1340
float和double不能直接进行运算 如银行系统等 float a1=0.1 double a2=0.1 系统判断a1和a2不相等 因为浮点数只是大约数，是离散的，有舍入误差，接近但不等于 所以最好完全避免浮点数进行比较 比较用 Bigdecimal数学工具类等进行计算 float a3=10000000000000; float a4=a3+1; 但是结果a3=a4 每一个字符本质还是数字 对应Unicode 65536的表（两个字节2^16=25536） 转义字符 \t 制表
为什么说“浮点数不可以比较大小”？(浅解)
2303_76783429的博客
04-22 378
首先，我们知道计算机都是用二进制来存储数据的，一个十进制的数比如 11 ，在二进制中可以表示为 1011，用科学计数法表示为 1 x 2^3 + 0 x 2^2 + 1 x 2^1 + 1 x 2^0 ，使用的转换方法是将十进制的数不断。，比如0.725 x 2 = 1.25，大于1，于是取1，二进制小数点后一位为1；同理十进制小数0.25 用二进制表示为 0.01 ，科学计数法表示 0 x 2^-1 + 1 x 2^-2，转换方法是将十进制的数不断。输出结果为： no, b = 200。
为什么浮点类型变量不能直接比较？而是用一个范围？
doujianyoutiao的博客
10-24 1478
并不是不可以，而是不推荐，因为容易出错。从下面的例子中能看出（true打印出来是1，false打印出来是0），由于浮点数有精度的问题，数值结果很容易出现偏差。f2 - 81.2不等于0是因为，f2是float类型的，字面量81.2默认是double，所以由于81.2到float类型已经精度不准了，减去精准的81.2得到的结果肯定也不准了。f1/5=f3也是一样的道理，但由于f2和f3都是81.2转过去的，所以这两是相等的，f3跟81.2是不相等。==0也是一样的道理。如果要比较，结合数据类型和自己要求的精度
float为什么不能直接用==作比较
yazhouren的专栏
01-05 4051
origin:https://www.jianshu.com/p/9f5a494d24cf 本文尝试着将以下内容做一个浅显的解释，主要包括浮点数为什么是不精确的，浮点数为什么不能用==和！=直接比较，以及浮点数的比较方法等几个方面。如果那个地方说的不对还请各位看官不吝赐教！欢迎大家评论区讨论。 IEEE 754 --- 二进制浮点数算术标准 浮点格式是一种数据结构，用于指定包含浮点数的字段，这些
两个浮点类型不可以直接判断相等以及解决方案
EricWZY2008的专栏
05-05 2281
在计算机中，浮点数在内存的存储方式和int型不同，浮点数在存储的时候会有舍入误差，所以不能直接在程序中直接比较两个浮点数相等，如果需要判断相等，则需要使用精度这个方式。 上面的代码输出的结果是： 程序并不会输出equation，原因就是a跟b并不相等。这个计算机的舍入误差。如果需要比较两个数相等，则需要使用精度来进行判断。 上面的代码输出结果是： 输出的结果达到了预期。 ...
【C语言】浮点型数据为什么不能直接比较
徐腾腾的博客
10-23 1864
编程细节：浮点型数值的比较 浮点型数值不能直接比较，要先定义一个极小值，如果两个数的差值小于这个极小值，则认为两个数相等 #define MIN 0.0000000001 //定义一个极小值 double temp = 2.5； if（abs（temp - 2.5） < MIN） { return ; } ...
浮点数比较大小（必须考虑精度）
本人很菜轻点骂
10-29 2959
在C++（以及其他很多编程语言）中，浮点数是以IEEE 754标准进行表示的。这种表示方法会导致浮点数运算中出现舍入误差，使得两个看似相等的浮点数在计算机内部的表示可能会有细微的差异。因此，直接比较两个浮点数是否相等是不安全的，可能会得到错误的结果。如需要对浮点数进行比大小，我们需要定义一个很小的正数（通常设置为10的-6次方），并判断两个浮点数之差的绝对值是否小于或等于这个很小的数来判断它们是否相等。浮点数是不能直接比较大小的。的判断浮点数相等的方法。
浮点数的大小比较为什么不能用等号？
weixin_33973609的博客
11-16 352
2019独角兽企业重金招聘Python工程师标准>>> ...
为什么浮点数不能直接与零值比较？谢谢
niepangu的专栏
04-11 2878
这是程序员面试的一道常见题，也是个C++基础问题。若只在大学里看过几本基础的编程入门书，看见这道题可能会觉得奇怪，不就是和0比较吗，直接拿出来比就是了，其实非也。下文引自google搜索结果，出处不详，高手可以无视，菜菜留下，记得做好笔记。  首先给个提示：题目中要求的是零值比较，而非与0进行比较，在C++里“零值”的范围可就大了，可以是0， 0.0 ，FALSE或者“空指针”。  ①
torch中浮点数可以直接比较大小吗
最新发布
08-08
在PyTorch中，可以直接使用比较运算符（如`==`、`!=`、`<`、`>`）对浮点数进行比较操作。这些运算符会逐元素地对张量中的浮点数进行比较，并返回一个布尔类型的张量，表示每个位置的比较结果。例如，若需要判断一个张量中哪些位置的元素等于0，可以使用`torch.eq(t, 0)`或直接使用`t == 0`，其中`t`为一个包含浮点数的张量[^1]。 需要注意的是，浮点数在计算机中的表示存在精度问题，因此在比较两个浮点数是否相等时，直接使用`==`可能会因为精度误差导致结果不准确。为了避免这种情况，可以使用`torch.isclose()`函数，它允许设置一个容差范围（通过`rtol`和` atol`参数），以判断两个浮点数是否“足够接近”，从而更可靠地进行相等性判断。例如： ```python import torch # 创建一个包含浮点数的张量 t = torch.tensor([[0.0, 1.0, 0.0], [2.0, 0.0, 3.0], [0.0, 4.0, 0.0]]) # 使用 == 直接比较 mask1 = t == 0.0 print("Using == 0.0:") print(mask1) # 使用 torch.isclose 比较 mask2 = torch.isclose(t, torch.tensor(0.0)) print("Using torch.isclose:") print(mask2) ``` 输出结果为： ``` Using == 0.0: tensor([[ True, False, True], [False, True, False], [ True, False, True]]) Using torch.isclose: tensor([[ True, False, True], [False, True, False], [ True, False, True]]) ``` 在上述示例中，`t == 0.0`和`torch.isclose(t, 0.0)`的结果是一致的，但在处理涉及浮点运算的结果时，推荐使用`torch.isclose()`以避免因精度问题导致的误判。 ### 总结 - 对于精确匹配，可以直接使用比较运算符如`==`，但在涉及浮点运算时需谨慎。 - 对于更鲁棒的浮点比较，应使用`torch.isclose()`，它允许一定的误差范围，从而避免精度问题带来的影响。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值