sas非线性回归

泰勒公式


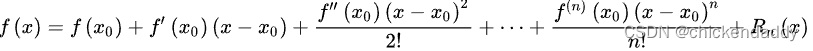
#举个栗子
假设要估计的函数为y=f(x,w)#y，x实则数据点，w为参数；
实际上就是f(x,w)和w间的关系，w成了自变量#实则f(w)，以高斯牛顿方法为栗子，先先预设一个w0，然后在w0这个点上用多元泰勒展开#根据w维数定，展开后取到二阶偏导项作为原来的近似，所以得到一个新的f1(w),然后直接用矩阵最小二乘公式找到一个新的w1，然后再展开循环下去；#每一步记录下残差平方和，找到一个收敛的残差平方和就结束。

*u检验，非参检验方法，检验两组样本是否来自同一数据总体，具体为获取各样本分数的次序#矩阵的秩,然后据此计算统计量u来评价两组平均名次是否具有显著差异。