推荐系统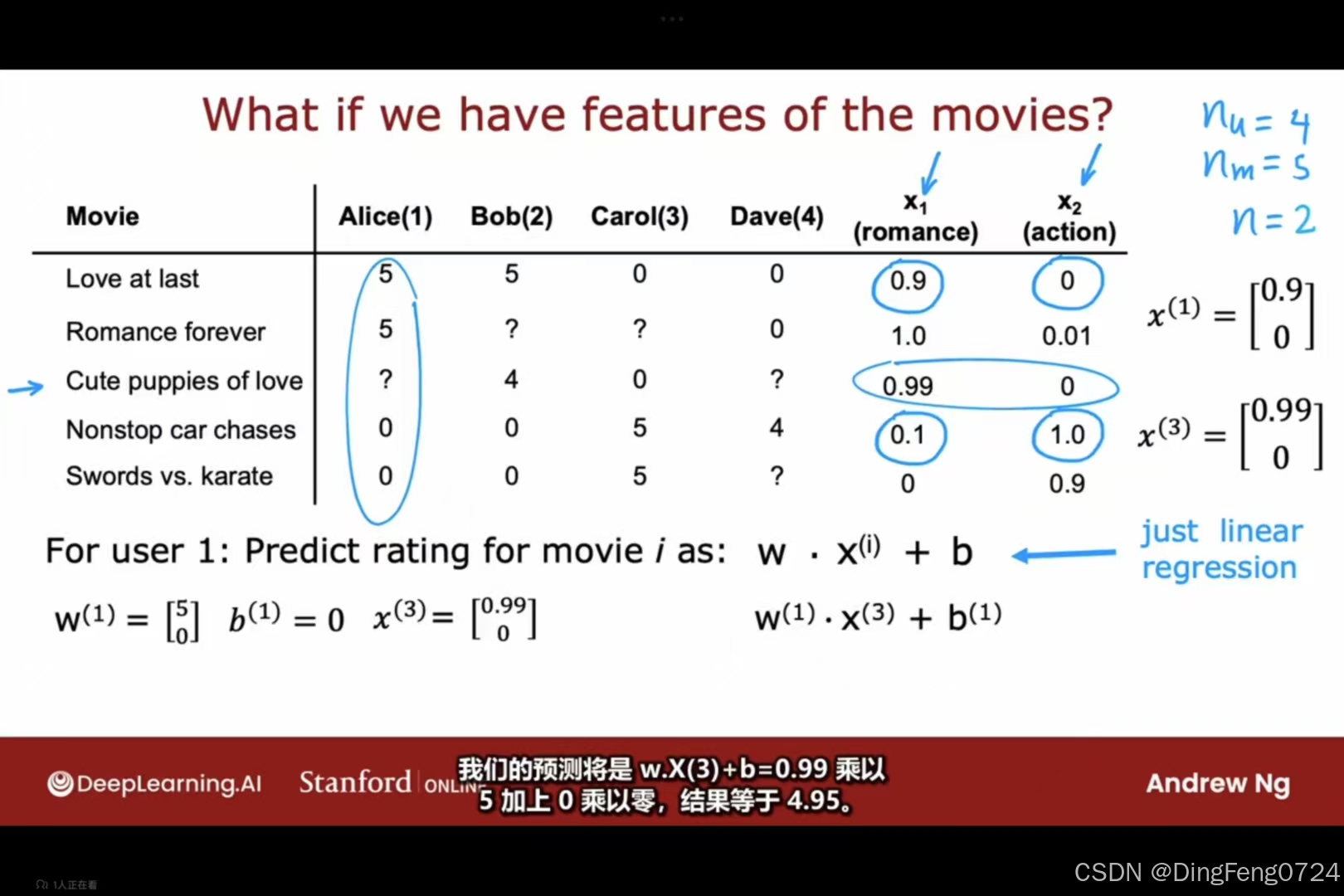
当我们拥有电影的特征值x1,x2时可以预测出用户对于为打分的电影的评分。对于用户j,而不仅仅是用户1,我们可以预测用户j对电影i的评分为w(j).X(i)+b(j)。

r i,j代表i是否对j进行评分,这是一个状态值通常为0或1.yi ,j代表用户i对于电影j所打的评分,而wb则是用户的特征值,mj则代表用户所评分的数量。
同样的我们也可以通过运算得到x1,x2
 协同过滤算法
协同过滤算法

图片描述了协同过滤(Collaborative Filtering)中电影特征 x(i) 的学习过程,与之前讨论的用户参数 w(j),b(j) 共同构成完整的推荐系统模型。
- 目标:通过用户评分数据 y(i,j),同时学习 电影特征 x(i) 和 用户参数 w(j),b(j),使预测评分逼近真实评分。
公式解析
1. 单个电影特征 x(i) 的成本函数

- 第一项:平方误差损失,衡量电影 i 对所有已评分用户 j 的预测误差。
- 第二项:L2正则化项,约束电影特征 x(i) 的大小,防止过拟合。
- 适用场景:仅优化某一部电影的特征 x(i),固定用户参数 w(j),b(j)。
2. 所有电影特征的成本函数(全局优化)

- 扩展逻辑:对所有电影 i=1,2,…,nm 的特征 x(i) 进行联合优化。
- 正则化调整:对每部电影的所有特征维度 k=1,2,…,n 进行约束。
优化方法
-
交替最小化(Alternating Minimization)
- 步骤1:固定电影特征 x(i),优化用户参数 w(j),b(j)(如之前讨论)。
- 步骤2:固定用户参数 w(j),b(j),优化电影特征 x(i)(如本图所示)。
- 交替迭代:重复上述步骤直至收敛。
-
梯度下降(Gradient Descent)
- 参数更新规则:

- 梯度计算:

- 参数更新规则:
协同过滤的完整框架
- 双向学习:
- 用户侧:学习 w(j),b(j),表示用户对电影特征的偏好和评分习惯。
- 电影侧:学习 x(i),表示电影的特征向量(如隐含的“动作片”“浪漫片”等维度)。

优化方法:交替最小化(Alternating Minimization)
由于直接联合优化 w,b,x 复杂度高,通常采用交替优化策略:
- 固定电影特征 x,更新用户参数 w(j) 和 b(j)。
- 使用梯度下降法:

- 使用梯度下降法:
- 固定用户参数 w,b,更新电影特征 x(i)。
- 梯度计算:
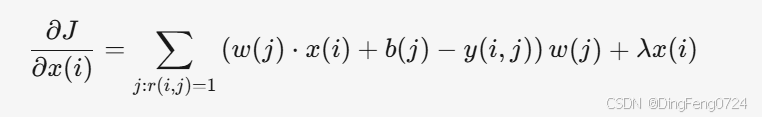
- 梯度计算:
- 交替迭代直至收敛。
二进制标签

对于用户的一些可能表现出喜欢的行为,我们对其打上标签即为0或1
 这个过程类似于将线性回归问题转换为逻辑回归问题,最终输出的数据是用户喜欢这一事件的概率。
这个过程类似于将线性回归问题转换为逻辑回归问题,最终输出的数据是用户喜欢这一事件的概率。
 均值归一化
均值归一化
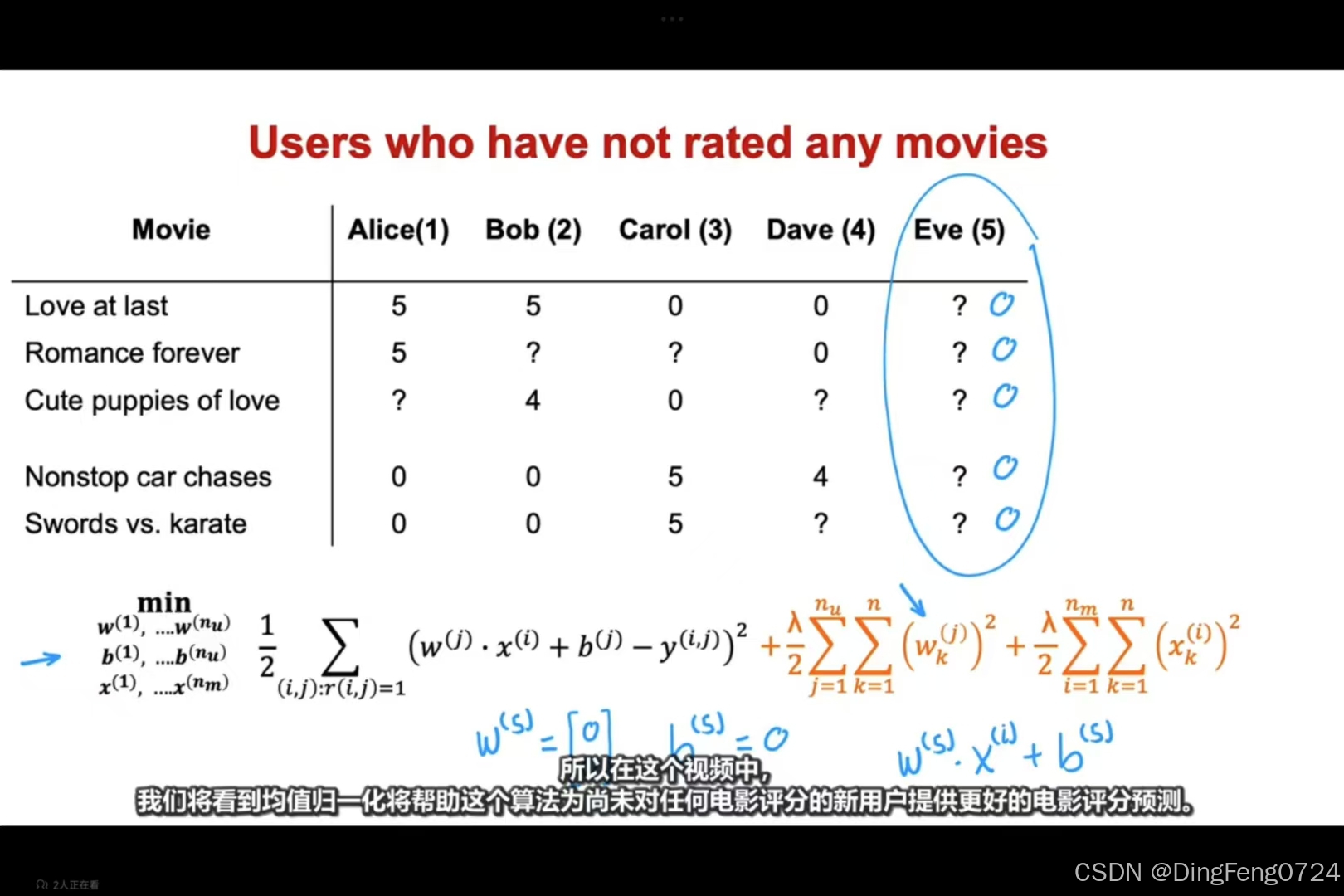 当用户的对于所有电影的评价状态都未知时我们可以通过均值归一化来解决如下问题。
当用户的对于所有电影的评价状态都未知时我们可以通过均值归一化来解决如下问题。
- 稀疏评分矩阵:用户对电影的评分存在大量缺失(如
?或0)。 - 新用户冷启动:用户未对任何电影评分时(如 Eve),如何预测其偏好。
- 算法优化:通过均值归一化提升预测准确性,尤其是针对未评分用户。
 这样在0维上数据之和便为0方便日后的预测、
这样在0维上数据之和便为0方便日后的预测、
若用户未对任何电影评分(如 Eve),模型无法通过常规协同过滤更新其参数 w(j),b(j)。
解决方案:
- 计算每部电影的平均评分:

- 例如,电影 Love at last 的平均评分:μ(1)=45+5+0+0=2.5(假设未评分项视为0)
- 归一化评分矩阵:
 仅对已评分项)
仅对已评分项) - 训练模型:使用 ynorm(i,j) 学习参数 w(j),b(j), x(i)。
- 预测时恢复均值:y^(i,j)=w(j)⋅x(i)+b(j)+μ(i)
优势:
- 新用户(如 Eve)的初始预测值为各电影的平均分 μ(i),避免因无评分导致的参数不更新问题。
- 提升模型对稀疏数据的鲁棒性。
实例演示(以用户 Eve 为例)
假设通过均值归一化后,模型预测 Eve 对电影的评分:
- 电影 Love at last:预测值 y^(1,5)=μ(1)=2.5。
- 电影 Nonstop car chases:假设模型学习到 Eve 的参数 w(5) 偏向动作片,预测值可能为 μ(4)+Δ。
代码实现
图片展示了如何通过自定义训练循环和自动微分,使用梯度下降算法优化参数 w 以最小化损失函数 J=(wx−1)2。以下是详细的解题思路与实现步骤:
1. 问题定义
- 目标:找到参数 w,使损失函数 J=(wx−1)2 最小化。
- 已知条件:
- 输入 x=1.0,目标值 y=1.0,因此 J=(w⋅1.0−1)2=(w−1)2。
- 偏置 b=0(简化问题,仅优化 w)。
- 最优解:当 w=1 时,J=0。
2. 梯度下降算法步骤
(1) 初始化参数与超参数
- 参数初始化:w 初始值通常随机设定(例如 w=0)。
- 学习率(α):α=0.01。
- 迭代次数:30 次(足够接近最优解)。
(2) 计算梯度
损失函数 J=(w−1)2 对 w 的梯度为:
∂w/∂J=2(w−1)
- 自动微分:使用 TensorFlow 的
GradientTape自动计算梯度,无需手动推导。
(3) 参数更新
每次迭代更新 w:
w:=w−α⋅∂w/∂J
伪代码实现
import tensorflow as tf
# 初始化参数
w = tf.Variable(0.0) # 初始值设为0
x = 1.0
y = 1.0
alpha = 0.01
iterations = 30
# 自定义训练循环
for iter in range(iterations):
with tf.GradientTape() as tape:
fwb = w * x # 前向计算:预测值 f(x) = w * x
cost = (fwb - y) ** 2 # 损失函数 J = (wx - 1)^2
# 自动计算梯度
[dJdw] = tape.gradient(cost, [w])
# 更新参数
w.assign_sub(alpha * dJdw)
print(f"Iteration {iter+1}: w = {w.numpy():.4f}, J = {cost.numpy():.4f}")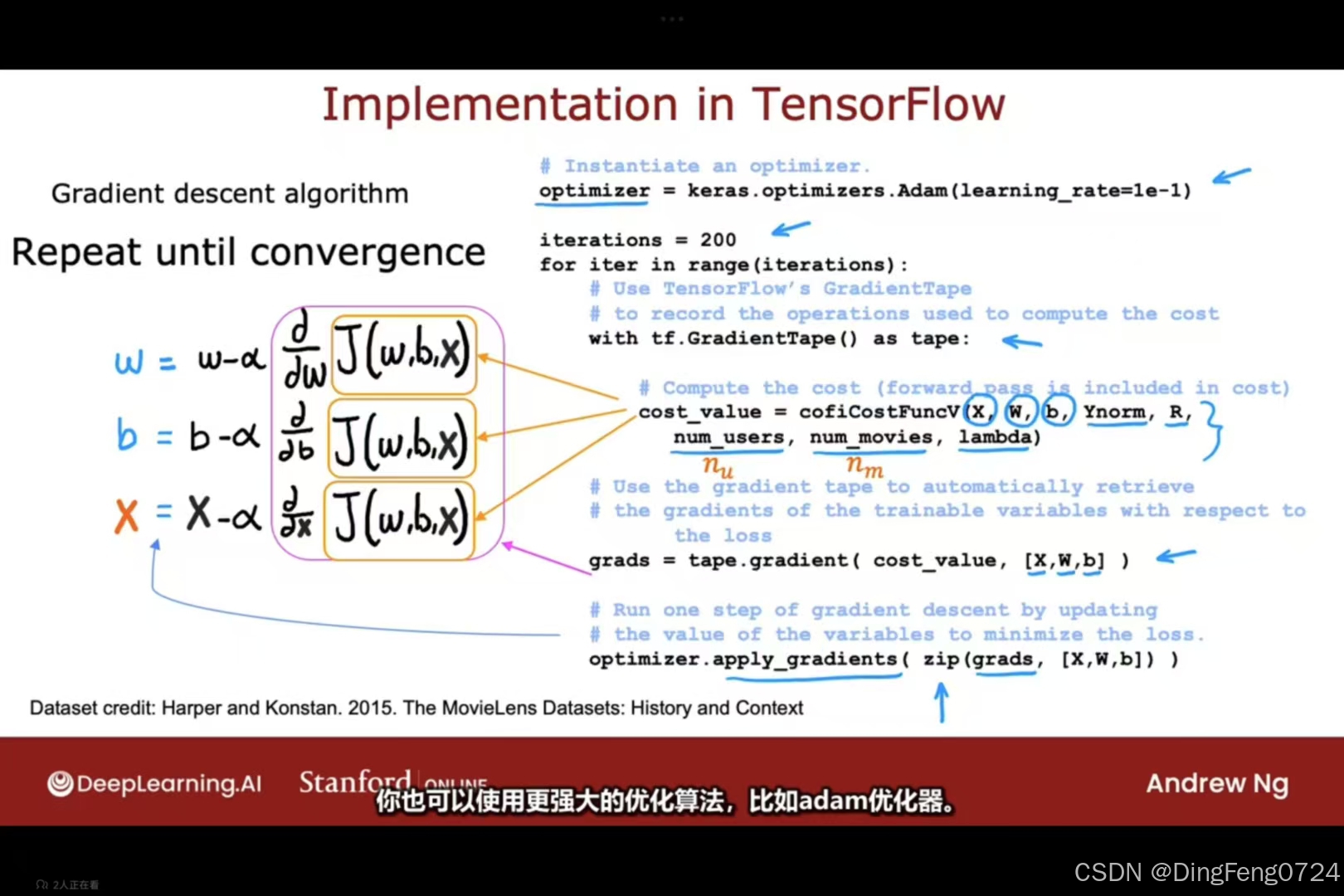 寻找相关特征
寻找相关特征
上文中我们学习了如何通过协同过滤算法来判断一个电影或者用户的特征值。
下面我们将要学习如何通过一个电影来找到一堆和他类似的电影。即寻找相关特征

基于内容的协同过滤
与协同过滤对比
| 维度 | 协同过滤 | 基于内容的过滤 |
|---|---|---|
| 核心逻辑 | "人以群分":通过相似用户群体行为推荐 | "物以类聚":通过用户/物品特征匹配推荐 |
| 数据依赖 | 用户-物品评分矩阵(稀疏性问题突出) | 用户画像、物品特征向量(冷启动更友好) |
| 典型公式 | y^(i,j)=θ(j)Tx(i) | y^(i,j)=θ(j)Tϕ(x(i)) |
| 符号说明 | θ(j):用户j的偏好参数 x(i):物品i的隐向量 | ϕ(x(i)):物品i的特征工程向量 |

 来构建一个用户特征,和电影特征。
来构建一个用户特征,和电影特征。
 那么通过用户i的特征vi和电影j的特征vj可以对他们进行点乘得到一个体现二者相关性的值。
那么通过用户i的特征vi和电影j的特征vj可以对他们进行点乘得到一个体现二者相关性的值。
但是用户的特征值一般都是偏多的,电影的特征值则不如用户特征值一样多i,很显然我们需要将二者转化为可以进行点乘的形式。
当当当当对二者进行构建一个神经网络
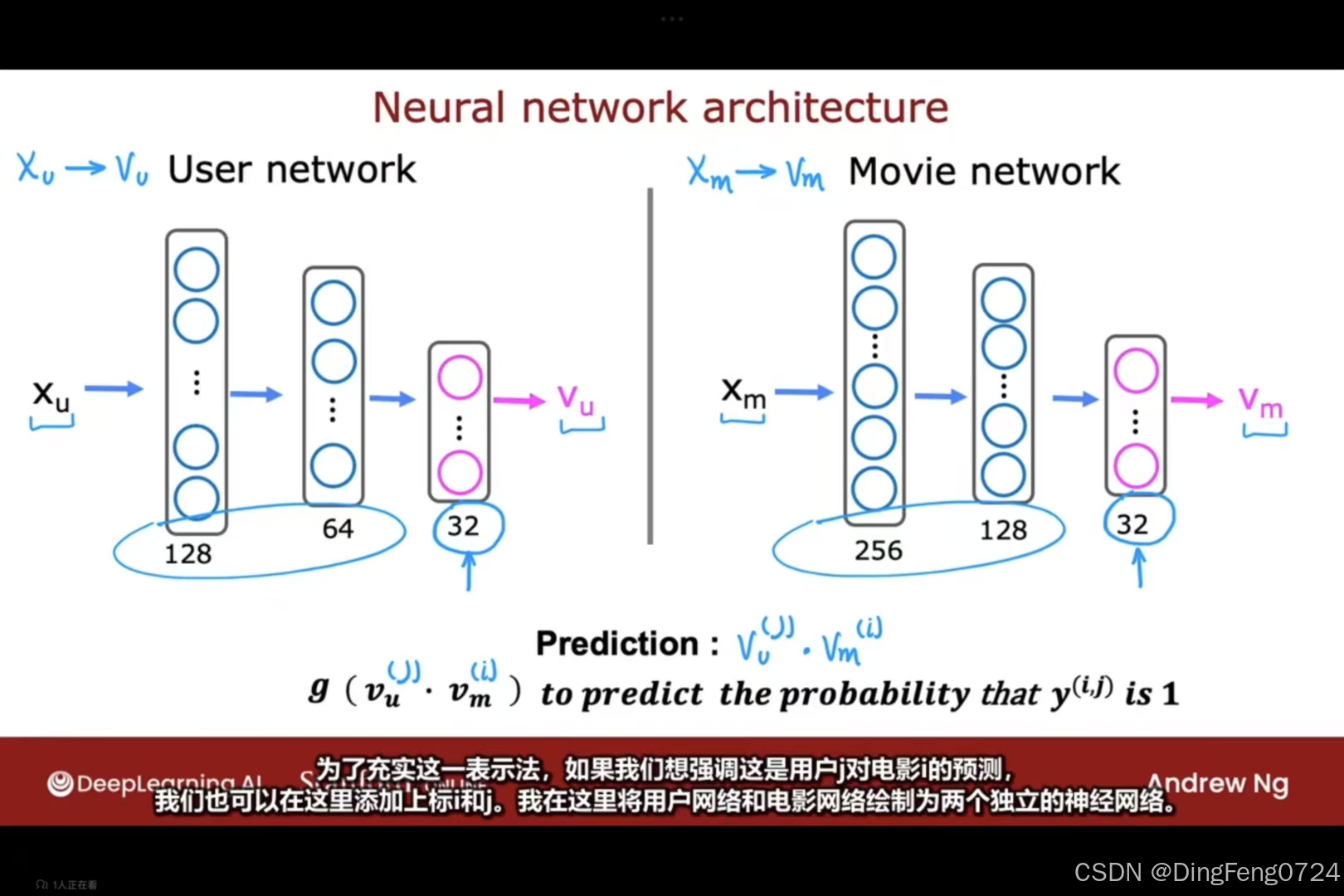
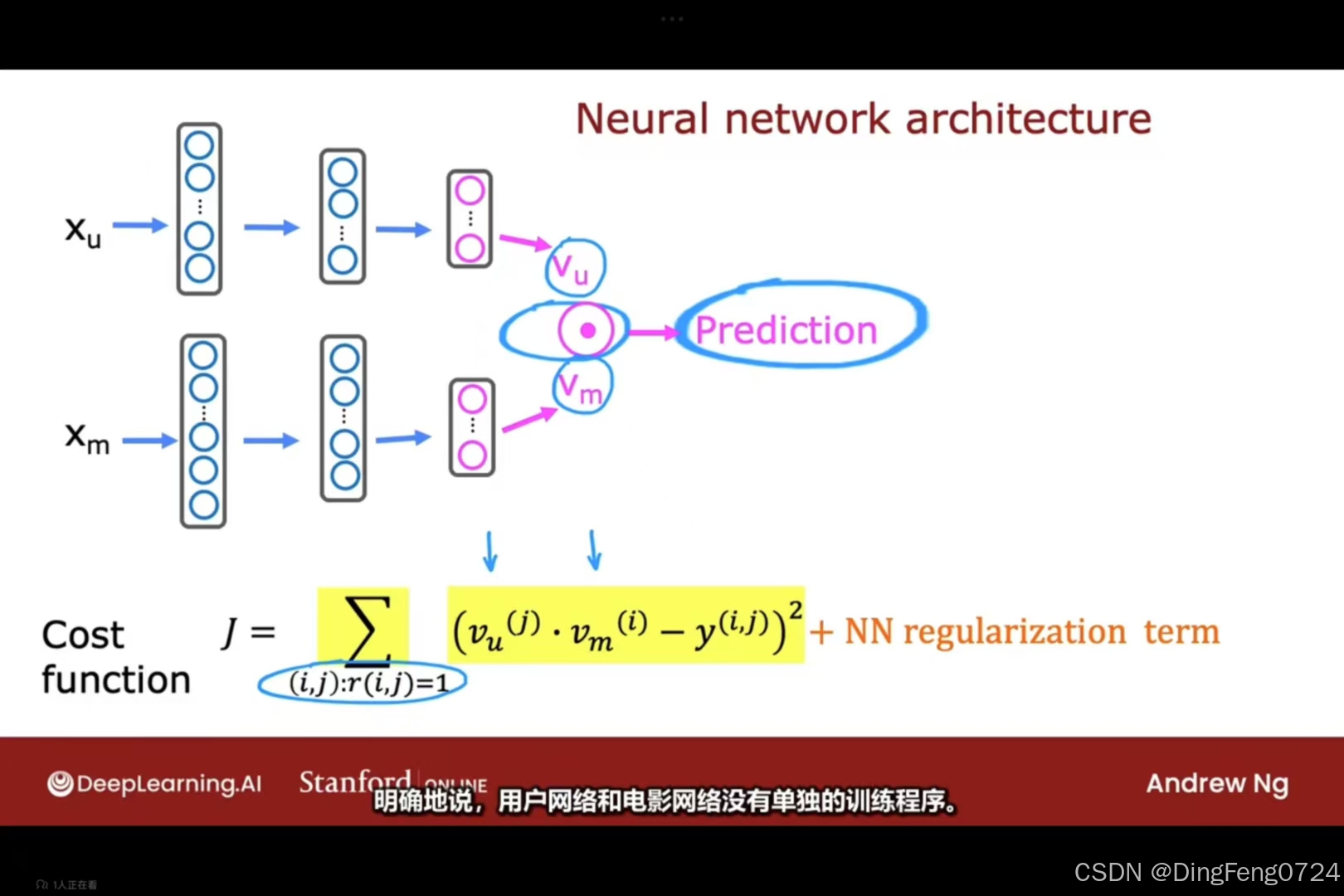 这样就可以进行点乘得到我们想要的那个预测值。
这样就可以进行点乘得到我们想要的那个预测值。
从大型目录中推荐
在上述应用中,我们所描述的算法有一个局限性,那就是如果你有一个包含许多不同电影的大型目录需要推荐,运行起来可能会非常耗费计算资源
 我们可以根据用户的特征值进行预先计算,从用户最近观看的10部电影 → 各找10部相似电影。
我们可以根据用户的特征值进行预先计算,从用户最近观看的10部电影 → 各找10部相似电影。
我们可以分为检索和排序两个步骤。
1. 检索阶段(Retrieval)
- 核心任务:从百万级候选池中快速筛选出千级候选集(图中示例约10秒完成)
- 关键技术:
- 多路召回机制:协同过滤(Xu)、内容匹配(Vm)、热门补足等并行计算
- 预计算优化:用户特征Xu和物品特征Vm离线计算存储,在线服务时直接调用
2. 排序阶段(Ranking)
- 数学模型:
y^=fθ(Xu,Vm)
其中:- Xu:用户特征向量(历史行为/人口属性/实时兴趣)
- Vm:物品嵌入向量(内容特征/协同过滤隐向量)
- fθ:排序模型(如DNN、Wide&Deep)
基于内容过滤的Tensorflow实现

一、模型架构原理
1. 双塔结构设计
- 用户塔(user_NN):
输入层(用户特征)→ Dense(256, ReLU) → Dense(128, ReLU) → Dense(32) → L2归一化 - 物品塔(item_NN):
输入层(物品特征)→ Dense(256, ReLU) → Dense(128, ReLU) → Dense(32) → L2归一化 - 相似度计算:
通过点积运算度量用户向量与物品向量的相关性:
similarity=vu⋅vmT
2. 归一化操作的意义
python
vu = tf.linalg.l2_normalize(vu, axis=1) # 用户向量归一化
vm = tf.linalg.l2_normalize(vm, axis=1) # 物品向量归一化- 数学本质:将向量投影到单位超球面,使点积等价于余弦相似度
- 计算优势:避免向量模长影响相似度计算,提升训练稳定性
二、代码实现精解
1. 网络构建要点
python
# 用户塔(修正代码中的拼写错误)
user_NN = tf.keras.models.Sequential([
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(32) # 最终嵌入维度
])
# 物品塔
item_NN = tf.keras.models.Sequential([
tf.keras.layers.Dense(256, activation='relu'),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dense(32)
])2. 特征交叉层解析
python
output = tf.keras.layers.Dot(axes=1)([vu, vm])- 该操作等价于:∑i=132vui×vmi
- 实际工程中可替换为:
output = tf.reduce_sum(vu * vm, axis=1, keepdims=True)
三、损失函数选择
1. 常用损失类型
| 损失函数 | 适用场景 | 数学表达式 |
|---|---|---|
| 均方误差(MSE) | 显式评分预测(如五星评分) | N1∑(y−y^)2 |
| 二元交叉熵 | 隐式反馈(点击/未点击) | −ylogy^−(1−y)log(1−y^) |
| Triplet Loss | 提升相似度对比区分度 | max(d(a,p)−d(a,n)+margin,0) |
2. 图中代码建议
原始代码片段存在缺失,推荐使用对比损失:
python
# 示例:基于批内负采样的对比损失
loss = tf.reduce_mean(
tf.math.softplus(- pairwise_similarities * labels)
)四、模型训练技巧
1. 特征工程建议
- 用户特征:历史行为序列、人口属性、实时兴趣
- 物品特征:内容标签、统计特征、知识图谱嵌入
- 处理技巧:
python
# 数值特征标准化 tf.keras.layers.Normalization(axis=-1) # 类别特征嵌入 tf.keras.layers.Embedding(input_dim=10000, output_dim=64)
2. 工业级优化方案
- 负采样策略:
每个正样本配比100-500个负样本(随机采样或困难负样本挖掘) - 混合精度训练:
python
tf.keras.mixed_precision.set_global_policy('mixed_float16') - 双塔更新策略:
用户塔高频更新(天级),物品塔低频更新(周级)
五、模型应用场景
1. 推荐系统候选生成
- 用户向量预计算 + ANN检索(如FAISS)实现毫秒级召回
- 排序公式:
\text{score} = \alpha \cdot \text{cosine_sim} + \beta \cdot \text{CTR_pred}
2. 跨域迁移学习
- 冻结用户塔,微调物品塔适配新业务场景
- 可视化案例:
python
# TSNE降维可视化 from sklearn.manifold import TSNE user_emb = TSNE(n_components=2).fit_transform(user_vectors)
减少特征数量-PCA-主成分分析
二维变一维
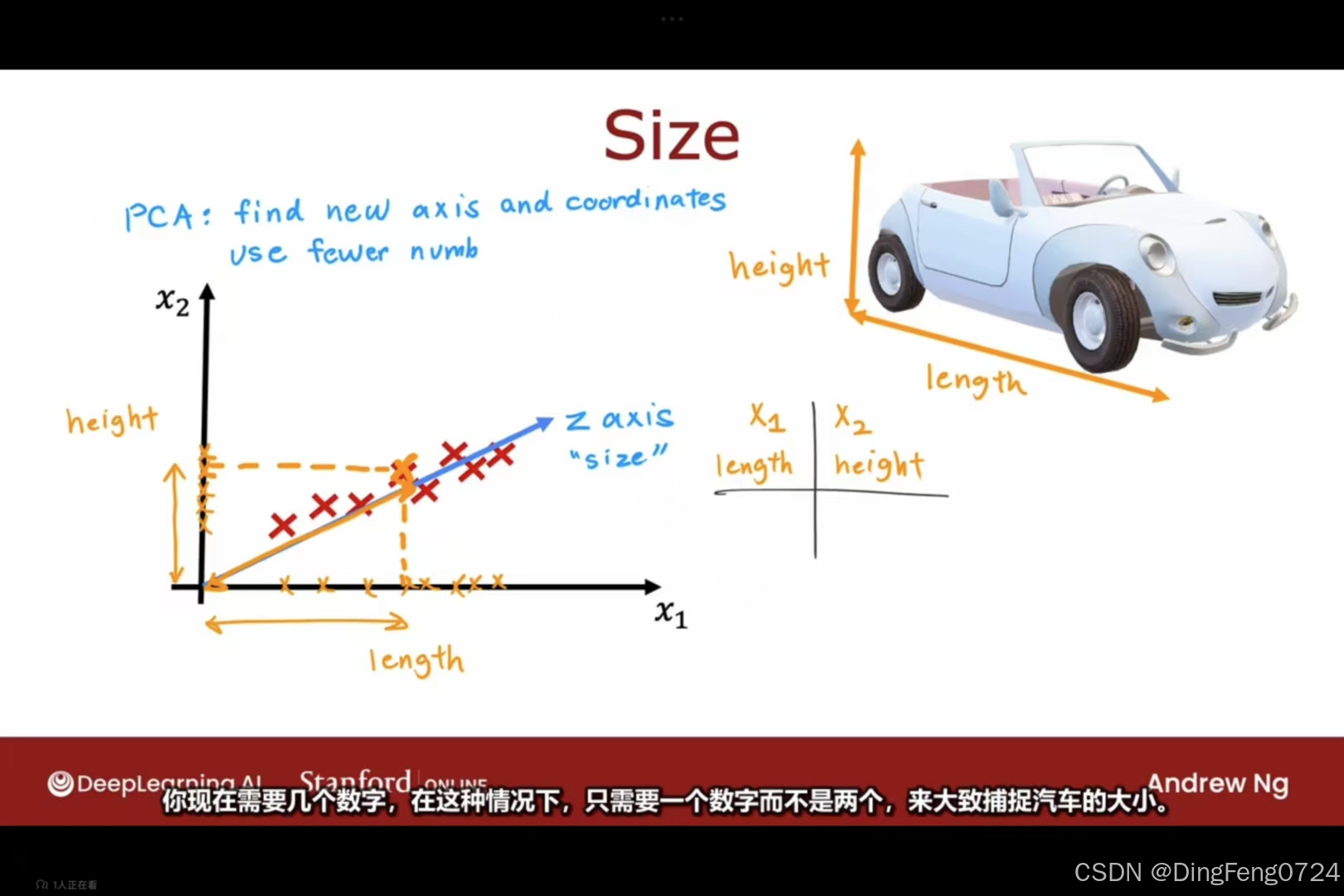 创建一个z轴可以较少损失的保存二维的数据
创建一个z轴可以较少损失的保存二维的数据
 首先进行归一化处理
首先进行归一化处理
 若数据的特征尺度差距很大,则进行特征缩放。
若数据的特征尺度差距很大,则进行特征缩放。
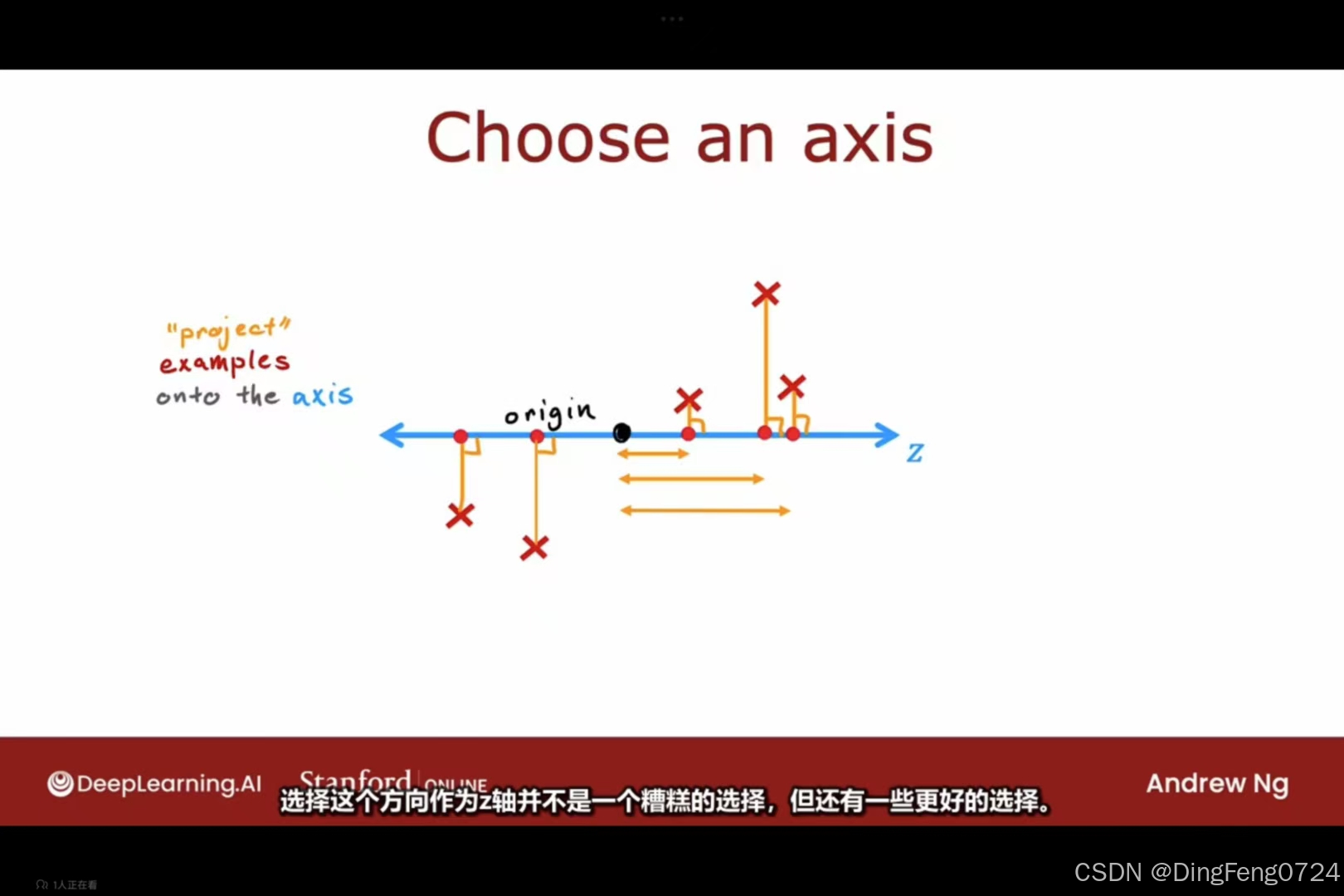
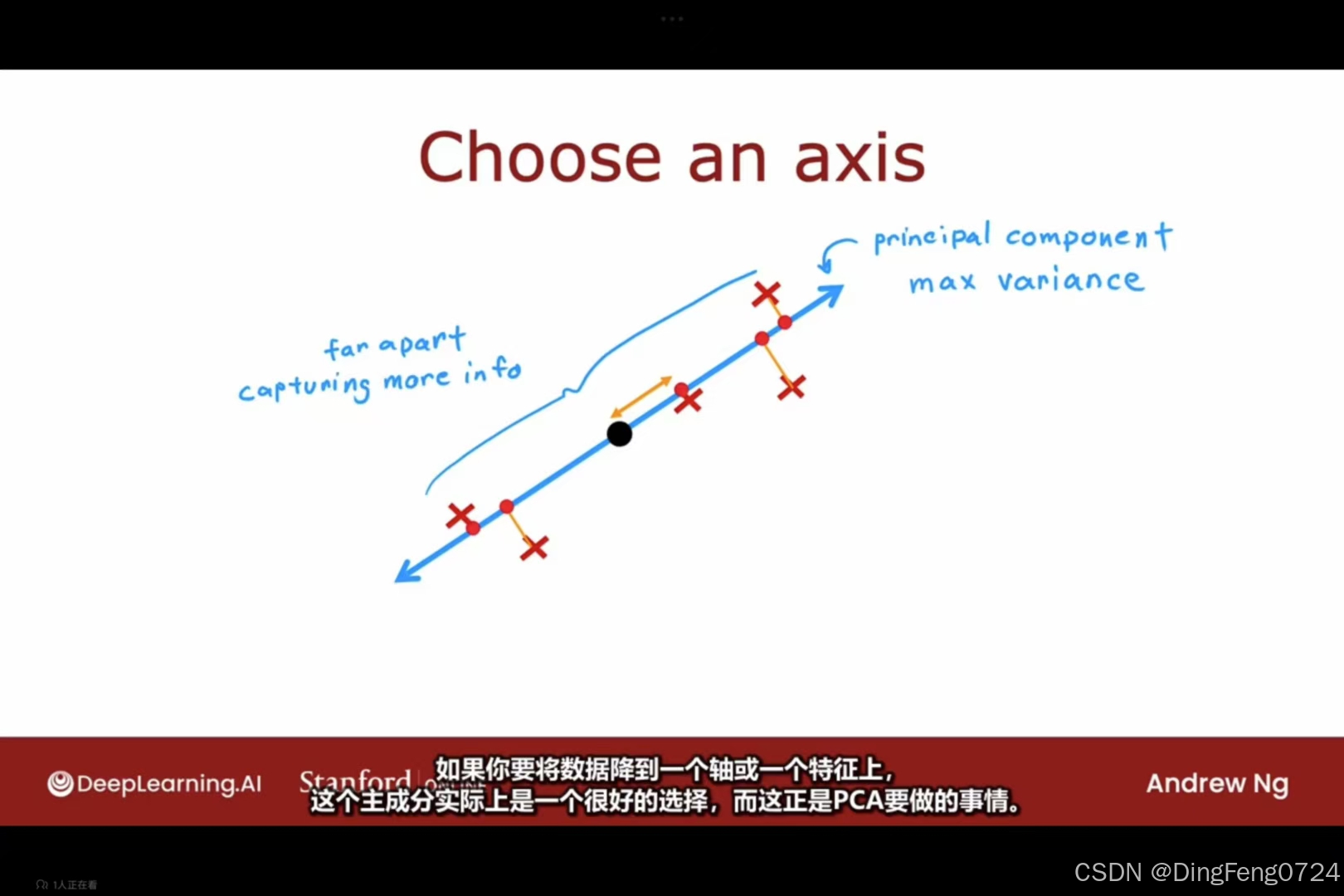 选择一个能使数据特征损失较少的轴
选择一个能使数据特征损失较少的轴
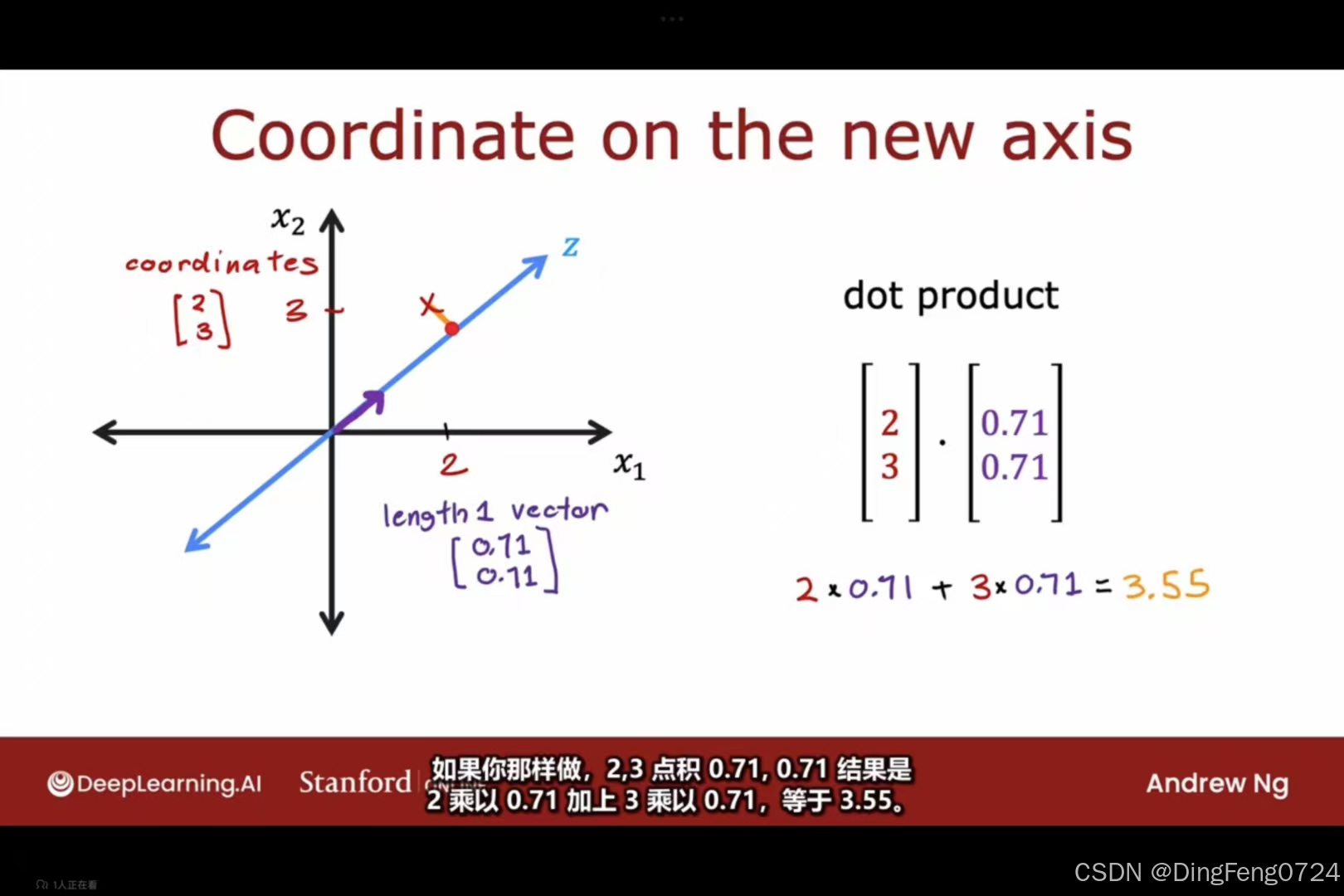 若长度为1的点坐标为二分之根号二,二分之根号二。将我们的原始数据和其点乘得到降维后的数据。
若长度为1的点坐标为二分之根号二,二分之根号二。将我们的原始数据和其点乘得到降维后的数据。
 第二个轴总是与第一个轴垂直。
第二个轴总是与第一个轴垂直。
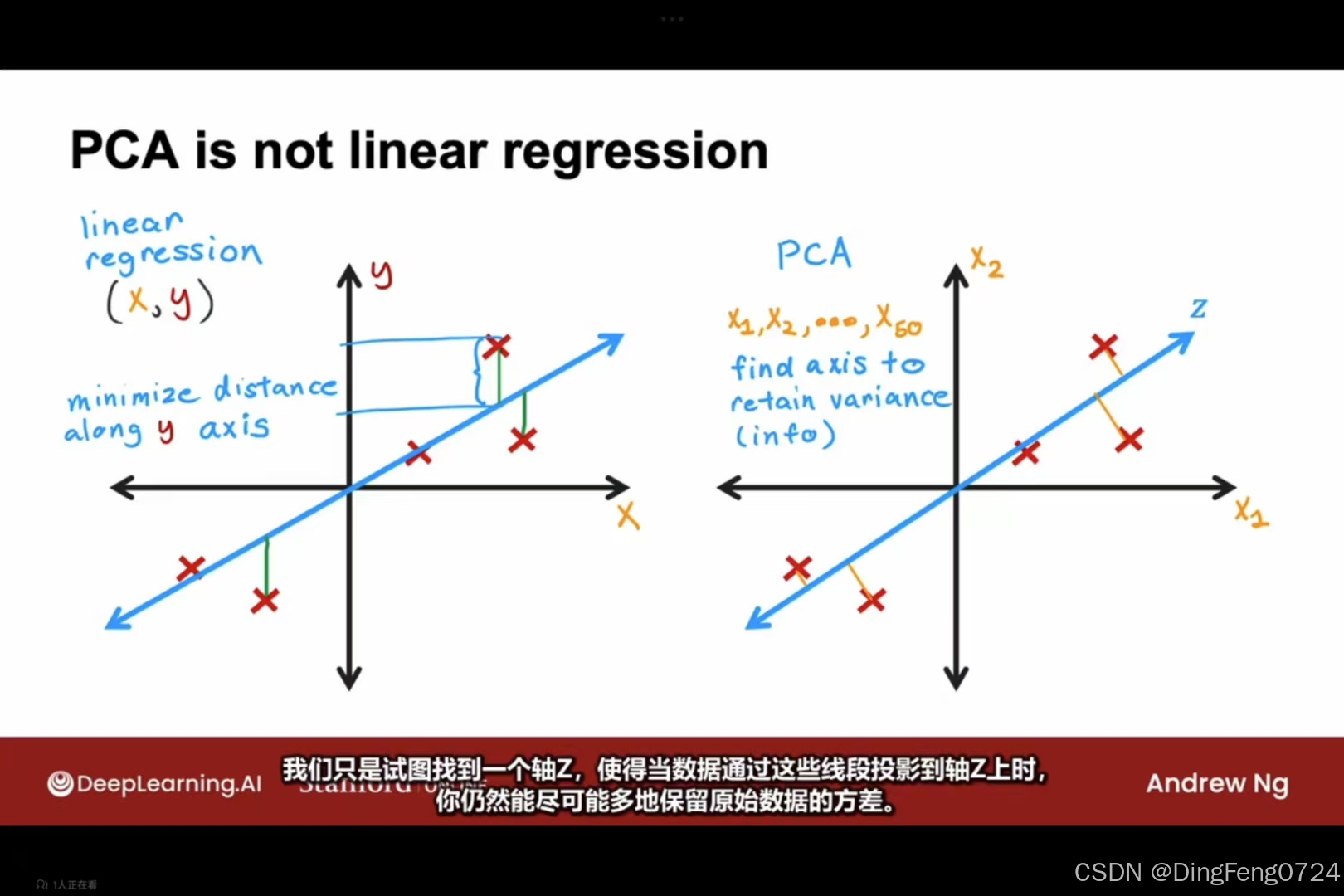
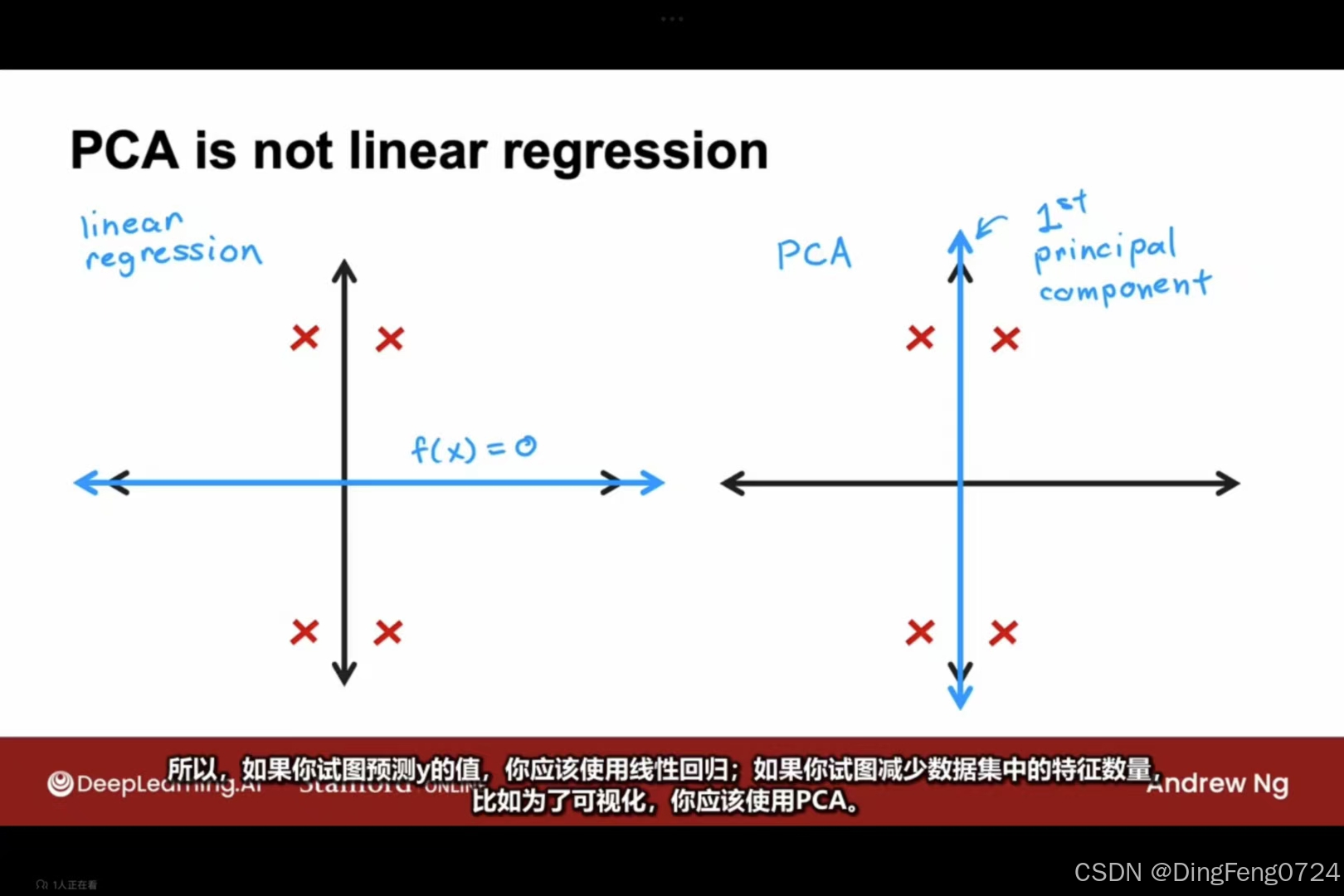
与线性回归之间的区别。
| 维度 | 线性回归 (Linear Regression) | 主成分分析 (PCA) |
|---|---|---|
| 任务类型 | 监督学习(有明确的目标变量y) | 无监督学习(无目标变量,仅分析数据内在结构) |
| 优化目标 | 最小化预测值y^与真实值y的垂直距离(沿y轴方向残差) | 最大化数据投影到低维空间后的方差(保留信息量最大) |
| 数学本质 | 条件均值建模:E(y∥X) | 协方差矩阵特征分解:Σ=n1XTX |
| 变量关系 | 区分自变量(X)与因变量(y) | 所有变量平等对待,无自变量/因变量区分 |
| 几何解释 | 寻找使垂直距离(图中蓝色线段)最小的超平面 | 寻找使正交投影距离(图中红色线段)最小的超平面 |
实现步骤

scikit-learn实现PCA完整流程(含代码模板)
python
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# 1. 数据预处理(特征缩放)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 消除量纲影响
# 2. PCA模型拟合(自动执行均值归一化)
pca = PCA(n_components=2) # 指定保留的主成分数
pca.fit(X_scaled) # 计算主成分方向
# 3. 检查方差解释率
print("各主成分方差解释率:", pca.explained_variance_ratio_)
plt.bar(range(2), pca.explained_variance_ratio_)
plt.title('方差解释率可视化')
plt.show()
# 4. 数据转换(降维投影)
X_pca = pca.transform(X_scaled) # 获得低维表示
# (可选) 逆向转换演示
X_reconstructed = pca.inverse_transform(X_pca)二、核心步骤技术解析
1. 特征缩放必要性
- 数学原理:PCA对协方差矩阵敏感,量纲差异会导致主成分偏移
- 标准化公式:
z=σx−μ - 代码细节:
StandardScaler同时完成均值归零和方差归一化
2. 主成分轴计算方法
- 协方差矩阵分解:
Σ=n1XTX=WΛWT- W:特征向量矩阵(主成分方向)
- Λ:特征值对角矩阵(方差量)
3. 方差解释率计算
- 计算公式:
解释率k=∑i=1pλiλk - 累计方差:
print("累计方差:", np.cumsum(pca.explained_variance_ratio_))
4. 投影的几何意义
- 线性代数本质:
Xpca=Xscaled⋅W[:,:k]- W:前k个特征向量组成的投影矩阵
三、可视化辅助理解
主成分方向可视化(示例代码)
# 绘制原始数据与主成分轴
plt.scatter(X_scaled[:,0], X_scaled[:,1], alpha=0.3)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
plt.arrow(0, 0, v[0], v[1], width=0.1, color='r')
plt.axis('equal')
plt.show()图示说明:红色箭头显示主成分方向,长度与方差量成正比
四、工业级应用技巧
-
主成分数选择:
- 肘部法则:选择累计方差≥85%的最小k值
pca = PCA().fit(X_scaled) plt.plot(np.cumsum(pca.explained_variance_ratio_)) plt.xlabel('主成分数量') plt.ylabel('累计方差解释率') -
稀疏数据优化:
- 使用
PCA(svd_solver='randomized')加速计算
- 使用
-
内存优化:
# 增量学习(处理大数据) pca = PCA(n_components=2) for batch in DataLoader: pca.partial_fit(batch)
五、常见问题解答
Q1:是否必须进行特征缩放?
- 必须执行:若特征量纲不同(如身高cm vs 体重kg),必须标准化
- 可省略:当所有特征已经是同量纲(如像素RGB值)
Q2:主成分的解释性?
- 非语义特征:主成分是数学最优解,需结合业务分析
- 特征贡献度:
pd.DataFrame(pca.components_, columns=feature_names)
Q3:与线性回归的区别?
- 投影方向差异:PCA最小化正交距离,回归最小化y轴距离(详见配图)

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








