信息/信息熵/相对熵/联合熵/条件熵/交叉熵/信息增益/信息增益率/基尼系数

信息

$I(X=x_i)=-{\log }_{2}p(x_i)$
公式中的负号是为了确保信息为0/正；
底数：只需满足大概率事件X对应于高的信息量即可。
I(x)：表示随机变量的信息；
p(x_i)：当x_i发生时的概率。
一个具体事件的信息量应该是随着其发生概率而递减的，且不能为负。

熵

在信息论和概率论中，熵度量随机变量的不确定性。熵又称为自信息(self-information)，可以视为描述一个随机变量的不确定性的数量。信息熵考虑随机变量的所有可能取值，即所有可能发生事件所带来的信息量的期望，计算公式：
$H(X)={\sum }_{i=1}^{n}p(x_i)I(x_i)=-{\sum }_{i=1}^{n}p(x_i){\log }_{b}p(x_i)$
如果n表示X变量取值种类，那么p(x_i)表示X变量取x_i值占总体样本的比例。
熵只依赖X的分布，和X的取值没有关系，熵是用来度量不确定性。熵越大，表明X=x_i的不确定性越大。反之亦然。在机器学习分类中，熵越大表明这个类别的不确定性更大，反之越小。当随机变量的取值为两个时，熵随概率的变化曲线如图：

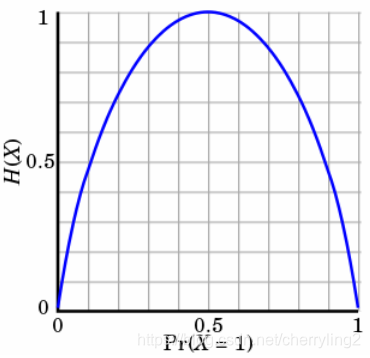
当p=0/1时，H§=0，随机变量完全没有不确定性；
当p=0.5时，H§=1，此时随机变量的不确定性最大。
示例：
X = [1 0 1 1 0] Y = [1 1 1 0 0]
p(X=0)=2/5 p(X=1)=3/5
p(Y=0)=2/5 p(Y=1)=3/5
$H(X)=-2/5\times \log (2/5)-3/5\times \log (3/5)=0.292$
$H(Y)=-2/5\times \log (2/5)-3/5\times \log (3/5)=0.292$

相对熵

相对熵(relative entropy)又称Kullback-Leibler差异(Kullback-Leibler divergence)或简称KL距离，是衡量相同事件空间里两个概率分布相对差距的测度。两个概率分布$p(x)$和$q(x)$的相对熵定义为：
$D(p||q)={\sum }_{x\in X}p(x)\log \frac{p(x)}{q(x)}$
该定义中约定$0\log \frac{0}{q(x)}=0$，$p(x)\log \frac{p(x)}{0}=\infty$。
表示成期望值为：
$D(p||q)=E_p(\log \frac{p(x)}{q(x)})$

交叉熵

如果一个随机变量$Xp(x)$，$q(x)$为用于近似$p(x)$的概率分布，那么随机变量X和模型q之间的交叉熵(cross entropy)定义为：
$H(X,q)=H(X)+D(p||q)=-{\sum }_{x}p(x)\log q(x)=E_p(\log \frac{1}{q(x)})$
由此，可以定义语言$L=(X_i)p(x)$与其模型q的交叉熵为：
$H(L,q)=-{\lim }_{n\to \infty }\frac{1}{n}{\sum }_{x_1^n}p(x_1^n)\log q(x_1^n)$
根据信息论的定理：假定语言L是静态(stationary)遍历的(ergodic)随机过程，L与其模型q的交叉熵计算公式就变为：
$H(L,q)=-{\lim }_{n\to \infty }\frac{1}{n}\log q(x_1^n)$
可以近似地采用如下计算方法：
$H(L,q)\approx -\frac{1}{n}\log q(x_1^n)$
困惑度perplexity：在设计语言模型时，通常用困惑度来代替交叉熵衡量语言模型的好坏。给定语言L的样本$l_l^n=l_1,...,l_n$，L的困惑度${PP}_q$定义为：
${PP}_q=2^{H(L,p)}\approx 2^{-\frac{1}{n}}$