动态规划

动态规划介绍

动态规划是一种功能强大的计算模式，其解决问题的方式是首先定义它的一组子问题，然后按照由小到大，以小问题的解答支持大问题求解的模式，依次解决所有的子问题，并最终得到原问题(最大子问题)的解答。

leetcode 32 

 思路：

设字符串长度为L，最长合法括号子字符串的长度为dp[L-1]。对于某个字符的下标k, dp[k]表示0到k的这个字符串中的最长合法括号子字符串的长度，也就是所谓的子问题。然后状态转移方程如下：

首先我们只需要对')'进行处理，因为额外添加一个'('并不影响最终的结果。然后需要分两种情况：

如果str[i-1]为'('，那么有：

dp[i] = dp[i-2]+2　，　也就是在substr(0,i-2)的基础上增加一对括号

如果str[i-1]为'), 那么有：

dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2 

可以考虑这种情况：()(())　,最终结果为6。str[i]的')'可能在之前存在一个'('与之对应，等式中dp[i-1]表示的是它们中间的那部分的合法括号长度，dp[i-dp[i-1]-2]表示的是它们之前的合法括号的长度，２表示的是添加了这一对括号长度加２。

然后从dp数组中选取出最大的值就是答案。

代码如下(需要注意三目运算符的优先级)：

int longestValidParentheses(string s) {
    if(s == "")
        return 0;
    int length = s.length();
    vector<int> dp(length,0);
    int m = INT_MIN;
    for(int i = 0; i < length; i++) {
        if(s[i] == ')' && i != 0) {
            if(s[i-1] == '(')
                dp[i] = (i-2>=0?dp[i-2]:0)+2;
            else if(s[i-1] == ')' && s[i-dp[i-1]-1] == '(')
                dp[i] = dp[i-1] + (i-dp[i-1]-2>=0?dp[i-dp[i-1]-2]:0) + 2;
        }
        m = max(m, dp[i]);
    }
    return m;
}

leetcode 72

思路：

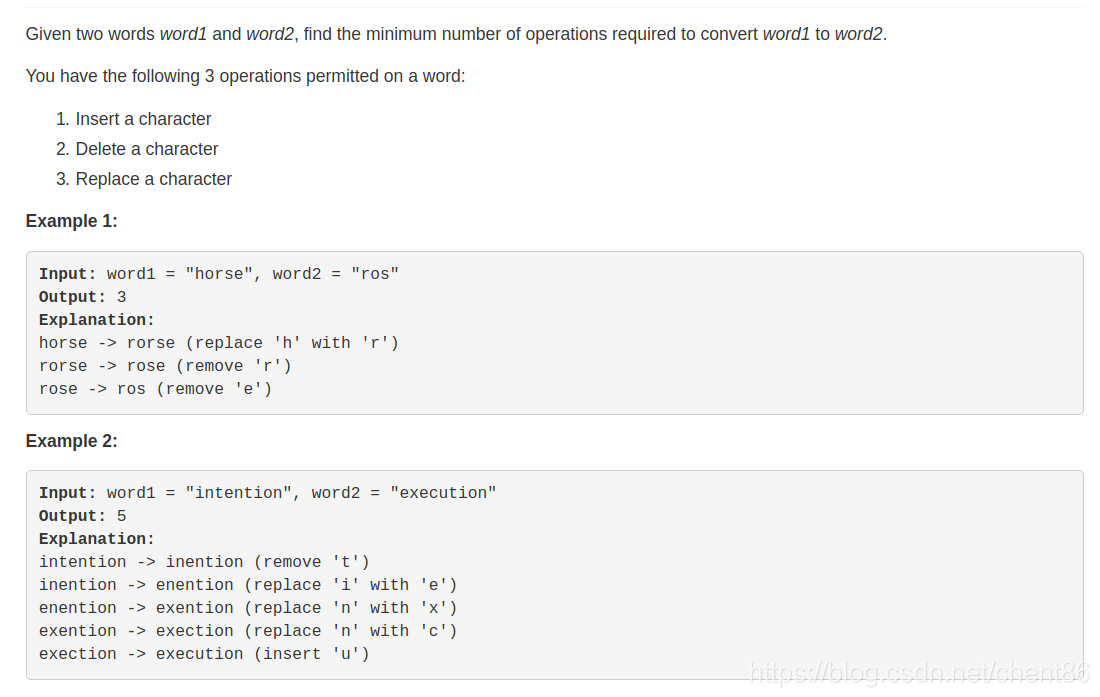
这一题是一道很典型的动态规划题目，然而很多解答并没有讲清楚各个转化方程的意义，以下是我的见解。我们将word1中前i个字符构成的字符串(str1)转变为word2中前j个字符构成的字符串(str2)需要的最小操作次数用dp[i][j]表示，设word1长度为m, word2长度为n, 则dp[m][n]就是最大子问题。

然后考虑子问题之间的转移方程：

如果str1和str2的最后一个字符相同，那么很显然，dp[i][j] = dp[i-1][j-1]

如果str1和str2的最后一个字符不同，根据题意，有三种操作：

删除：

假设我们知道str3(str3为str1删除最后一个字符后得到的字符串)转化为str2的开销(即dp[i-1][j])，那么str1在同样的转换之后，后面也就只多出一个字符，删除即可，开销加１

dp[i][j] = dp[i-1][j] + 1

增添：

假设我们知道str1转化为str3的开销(str3为str2删除最后一个字符得到的字符串)，即dp[i][j-1]，那么str1在这个转换的基础上，再加上str2的最后一个字符，就得到str2了,开销加1。

dp[i][j] = dp[i][j-1] + 1

替换:

假设我们知道str3(str3为str1删除最后一个字符后得到的字符串)转换为str4(str4为str2删除最后一个字符得到的字符串)的开销，那么在这个基础上，我们只要加上str2最后的一个字符即可，实际上就是把str1的最后一个字符替换为str2的最后一个字符，开销加1

dp[i][j] = dp[i-1][j-1] + 1

综上，dp[i][j]可以有三种从子问题的求解的方法，我们当然要选取开销最小的方法，故有：

dp[i][j] = min ( dp[i-1][j] + 1, min( dp[i][j-1] + 1, dp[i-1][j-1] + 1 ) )

可以看到，i的范围为[1, m],  j的范围为[1,n]，我们还需要提供边界的dp值。

很显然，对于dp[i][j], 如果i = 0, 那么dp[0][j] = j (空字符串到word2的子字符串，进行增添操作) ；如果j = 0, 那么dp[i][0] = i (从word1的子字符串到空字符串，进行删除操作)

代码如下：

int minDistance(string word1, string word2) {
    int m = word1.length();
    int n = word2.length();
    if(m == 0 && n == 0)
        return 0;
    vector<vector<int>> dp(m+1, vector<int>(n+1,0));
    for(int i = 0; i <= m; i++)
        dp[i][0] = i;
    for(int i = 0; i <= n; i++)
        dp[0][i] = i;
    for(int i = 1; i <= m; i++)
    for(int j = 1; j <= n; j++) {
        if(word1[i-1] == word2[j-1])
            dp[i][j] = dp[i-1][j-1];
        else
            dp[i][j] = min(dp[i-1][j]+1, min(dp[i][j-1]+1, dp[i-1][j-1]+1)); 
    }
    return dp[m][n];
}

leetcode 87

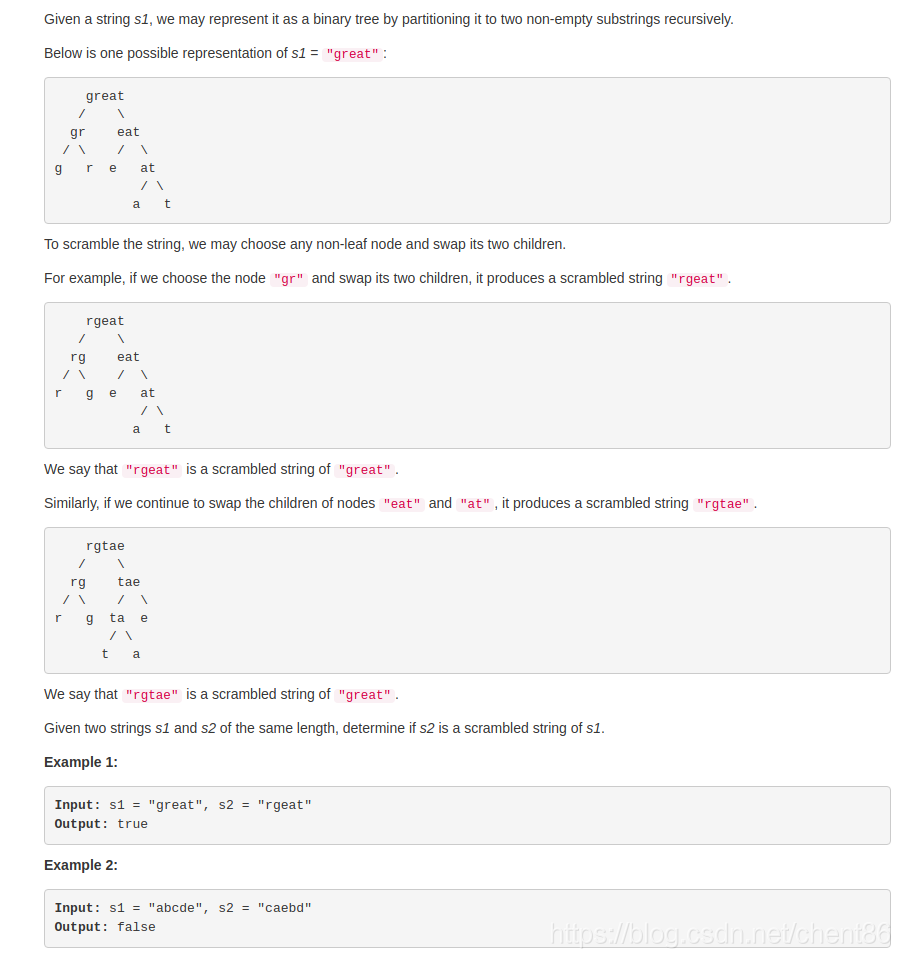
思路：

可以尝试使用递归的思想，对于两个字符串，我们将他们都分为两段，str1分为str1_a+str1_b, str2分为str2_a+str2_b,  如果他们是相互scramble得到的，那么存在两种情况：

一、scramble在这一层已经进行了，那么str1_a和str2_b为相互sramble的结果，str1_b和str2_a也是

二、scramble在这一层还没有进行，那么str1_a和str2_a为相互sramble的结果，str1_b和str2_b也是

所以我们只需要对他们的子字符串进行继续判断，也就将原问题化为更小的子问题了。

代码如下,其中运用好substr函数可以简化代码过程（如果只输入一个参数，代表从这个index到末尾的子字符串，这一点平时可能用得少）

bool isScramble(string s1, string s2) {
    if(s1 == s2)
        return true;
    if(s1.length() != s2.length())
        return false;
    int length = s1.length();
    int count[26] = {0};
    for(int i = 0; i < length; i++) {
        count[s1[i]-'a']++;
        count[s2[i]-'a']--;
    }
    for(int i = 0; i < 26; i++)
        if(count[i] != 0)
            return false;
    for(int i = 1; i < length; i++) {
        if(isScramble(s1.substr(0,i), s2.substr(0,i)) && isScramble(s1.substr(i), s2.substr(i)))
            return true;
        if(isScramble(s1.substr(0,i), s2.substr(length-i)) && isScramble(s1.substr(i), s2.substr(0,length-i)))
            return true;
    }
    return false;
}

然后考虑使用动态规划的方法，使用dp[i][j][k]表示子字符串s1.substr(i,k)与子字符串s2.substr(j,k)是否是相互scramble。那么最大的子问题即dp[0][0][length], length为初始时字符串的长度。然后实际上关键的步骤还是和上面的递归一样，分为两种情况。

总的来说，动态规划很强大，但是如何转化为子问题，如何列出状态转移方程并不容易想到，还需多练。

代码如下(搬运，侵删)：

bool isScramble(string s1, string s2) {
    if(s1.size() != s2.size()) return false;
    if(s1.size() == 0) return true;
    int n = s1.size();
    bool dp[n][n][n+1];
    for(int l = 1 ; l <= n ; l++)
    {
        for(int i = 0 ; i < n-l+1; i++)
        {
            for(int j = 0 ; j < n-l+1 ; j++)
            {
                if(l == 1)
                {
                    if(s1[i] == s2[j]) dp[i][j][l] = true;
                    else dp[i][j][l] = false;
                    continue;
                }
                
                dp[i][j][l] = false;
                for(int k = 1; k <= l-1; k++)
                {
                    if( (dp[i][j][k] && dp[i+k][j+k][l-k]) || (dp[i][j+l-k][k] && dp[i+k][j][l-k])  )
                    {
                        dp[i][j][l] = true;
                        break;
                    }
                }
            }
            
        }
    }
    return dp[0][0][n];
}