c++背包问题讲解

原创已于 2025-08-12 17:12:52 修改 · 1.7k 阅读

31 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #开发语言

于 2025-08-12 16:59:21 首次发布

背包问题讲解(#^ . ^#)

一.引入

假如你现在是个小偷，你去了一个超市去偷东西，但是你现在只有一个容量有限的背包，也就是说，你最多只能偷走有限的东西

所以你手法熟练的你需要：

1.拿去容积小的东西

2.拿去价值大的东西

但是，会出现一些特殊情况，比如你面前有一个价值小但容量也小的物品，还有一个容量大但价值也大的东西，这就让你很难办，所以聪明的你掏出了一个笔记本电脑快速写出背包问题代码，来帮助你选择。所以说，背包问题在生活中很常见，很容易考

二.概述

背包问题是动态规划的经典问题之一。背包问题指在一个有容积或重量限制的背包中放入物品，物品有体积、重量、价值等属性，要求在满足背包限制的情况下放置物品，使背包中物品的价值之和最大。根据物品限制条件的不同，背包问题可分为01背包、完全背包、多重背包、分组背包和混合背包等。

在这里插入图片描述

三.内容讲解

1. 01背包问题空间优化

求解第i行时，只需要第i-1行的结果，前面的结果已经没用了。求解c[i][j]时，只需要上一行j列或上一行j-w[i]列的结果。是否可以进行空间优化？

c[n][W]就是不超过背包容量时可以放入物品的最大价值（最优值）。若还想知道具体放入了哪些物品，怎么办呢？

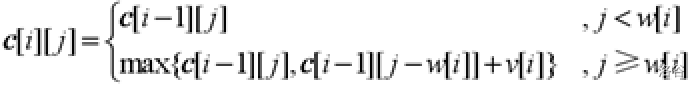
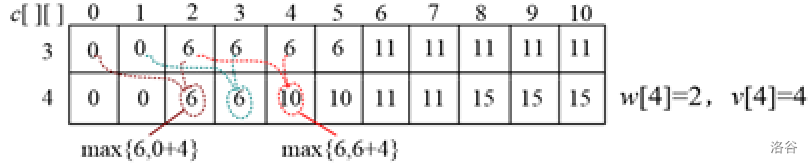
在这里插入图片描述

例如，处理第4种物品（w[4]=2，v[4]=4）时，只需第3种物品的处理结果（上一行）。求第j列时，若j<w[4]，则照抄上一行；若j≥w[4]，则需要将上一行第j列的值与上一行第j-w[4]列的值+v[4]取最大值。

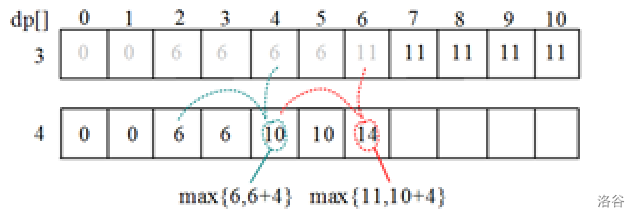
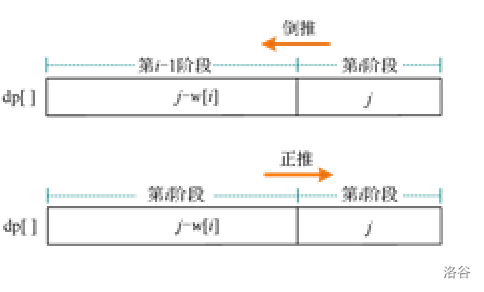
在这里插入图片描述

只需上一行当前列和前面列的值，因此只用一个一维数组倒推即可。

状态表示：dp[j]表示将物品放入容量为j的背包中可以获得的最大价值。

状态转移方程：dp[j]=max{dp[j],dp[j-w[i]]+v[i]}。

为什么不正推？？？

在这里插入图片描述

完全背包

给定n种物品，每种物品都有重量wi和价值vi，其数量没有限制。背包容量为W，求解在不超过背包容量的情况下如何放置物品，使背包中物品的价值之和最大。

状态表示：dp[j]表示将物品放入容量为j的背包中可以得的最大价值。

状态转移方程：dp[j]=max{dp[j],dp[j-w[i]]+v[i]}。

完全背包问题，每种物品有无限个，可以多次放入，采用正推形式求解。

在这里插入图片描述

P1616 疯狂的采药

#include<bits/stdc++.h>
using namespace std;
long long  t,m,w[100005],v[100005],dp[10000005];
int main(){
	cin>>t>>m;
	for(int i=1;i<=m;i++){
		cin>>w[i]>>v[i];//输入时间和价值； 
	}
	for(int i=1;i<=m;i++){
		for(int j=w[i];j<=t;j++){//完全背包用正推; 
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	cout<<dp[t];
	return 0;
	}

多重背包

多重背包:给定n种物品，每种物品都有重量wi和价值vi，第i种物品有ci个。背包容量为w，求解在不超过背包容量的情况下如何放置物品，使背包中物品的价值之和最大。

可以通过暴力拆分或二进制拆分将多重背包问题转化为01背包问题，也可以通过数组优化解决可行性问题。

1.暴力拆分指将第i种物品看作ci种独立的物品，每种物品只有一个，转化为01背包问题。

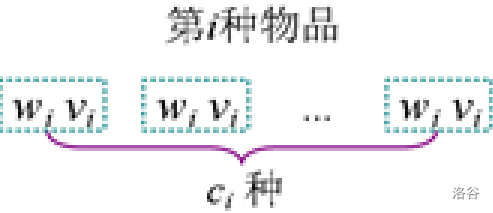
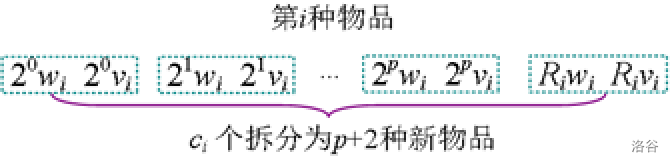
在这里插入图片描述
.
.
.

2.二进制拆分：将 $c [i]$ 个物品拆分成若干种新物品。存在一个最大的整数p，使 $20 + 21 + 22 + \dots + 2 p \leq c [i]$ 。将剩余部分用 $R_i$ 表示， $R_i=c[i]-(20+21+22+…+2p)$ ，将c[i]拆分为 $p + 2$ 个数：20,21,22,…, $2 p$ , $R_i$ 。

在这里插入图片描述

分组背包

给定n组物品，第i组有 $c_i$ 个物品，第 $i$ 组的第 $j$ 个物品有重量 $w [i] [j]$ 和价值 $v [i] [j]$ ，背包容量为 $W$ ，在不超过背包容量的情况下每组最多选择一个物品，求解如何放置物品可使背包中物品的价值之和最大。

状态表示：c[i][j]表示将前i组物品放入容量为j的背包中可以获得的最大价值。对第i组物品的处理状态如下：

不放入第i组物品，转化为“将前i?1组物品放入容量为j的背包中可以获得的最大价值”，最大价值为c[i-1][j]。

放入第i组的第k个物品，则转化为“将前i?1组物品放入容量为j-w[i][k]的背包中可以获得的最大价值”，获得的最大价值是c[i-1][j-w[i][k]]，再加上第i组的第k个物品获得的价值v[i][k]，总价值为c[i-1][j-w[i][k]]+v[i][k]。

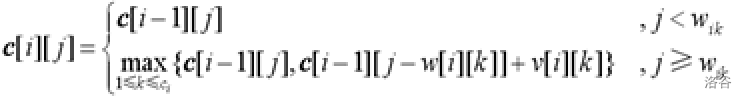
在这里插入图片描述

和01背包一样，将分组背包优化为一维数组，然后倒推，从第i-1阶段向第i阶段转移时每组最多选择一个物品。

状态表示：dp[j]表示放入容量为j的背包时可以获得的最大价值。

状态转移方程：dp[j]=max(dp[j],dp[j-w[i][k]]+v[i][k])。

混合背包

如果在一个问题中有些物品只可以取1次（01背包），有些物品可以取无限次（完全背包），有些物品可以取的次数有一个上限（多重背包），则该种问题属于混合背包问题。

四.代码实现

01背包

for(int i=1;i<=n;i++)//计算c[i][j]
    for(int j=1;j<=W;j++){
        if(j<w[i])//当物品的重量大于背包的容量，则不放此物品
            c[i][j]=c[i-1][j];
        else//否则比较此物品放与不放是否能使得背包内的价值最大
            c[i][j]=max(c[i-1][j],c[i-1][j-w[i]]+v[i]);
void opt2(int n,int W){
    for(int i=1;i<=n;i++)
        for(int j=W;j>=w[i];j--)//逆向循环（倒推）
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

完全背包

void comp_knapsack(int n,int W){
    for(int i=1;i<=n;i++)//完全背包 
        for(int j=w[i];j<=W;j++)//正序循环（正推）
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}

分组背包

void group_knapsack(int n,int W){
    for(int i=1;i<=n;i++)//分组背包 
        for(int j=W;j>=0;j--)// 
            for(int k=1;k<=c[i];k++){//枚举组内各个物品 
                if(j>=w[i][k]){ 
                    dp[j]=max(dp[j],dp[j-w[i][k]]+v[i][k]);
                }
            }
}

多重背包

void multi_knapsack1(int n,int W){//暴力拆分，容易超时！
    for(int i=1;i<=n;i++)
        for(int k=1;k<=c[i];k++)//多一层循环 
            for(int j=W;j>=w[i];j--)
                dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
void multi_knapsack2(int n,int W){//二进制拆分 
    for(int i=1;i<=n;i++){
        if(c[i]*w[i]>=W){//转化完全背包 
            for(int j=w[i];j<=W;j++)
                dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
        }else{
            for(int k=1;c[i]>0;k<<=1){//二进制拆分 
                int mn=min(k,c[i]);
                for(int j=W;j>=w[i]*mn;j--)//转化01背包 
                    dp[j]=max(dp[j],dp[j-w[i]*mn]+v[i]*mn);
                c[i]-=mn;
            }
        }
    }
}