数据结构与算法-树和森林（Tree and Forest）

4 树和二叉树（Tree and Binary Tree）

4.5 树和森林（Tree and Forest）

4.5.1 树的存储结构

1. 双亲表示法

以一组连续的存储单元存储树的结点，每个结点除了数据域 data 外，还附设一个 parent 域用以指示其双亲结点的位置。

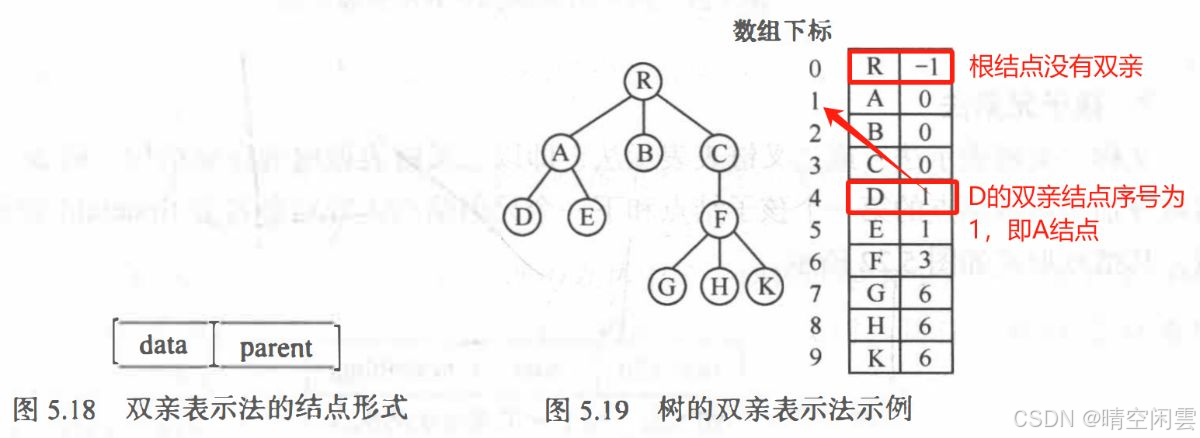
优缺点：

• 优点：查找结点的双亲十分方便，也很容易查找树的根。
• 缺点：查找结点的孩子时需要遍历整个结构。

代码实现：

typedef char TElemType;

// 双亲表示法结点结构
typedef struct PTNode
{
    TElemType data;
    int Parent; // 双亲位置域
} PTNode;

// 双亲表示法树结构
#define MAX_TREE_SIZE 100
typedef struct
{
    PTNode nodes[MAX_TREE_SIZE];
    int r; // 根结点的位置
    int n; // 结点的数量
} PTree;

创建一颗上图示例的树：

	PTree tree;
    tree.n = 10; // 结点数量
    tree.r = 0;  // 根结点位置

    // 按图片初始化
    tree.nodes[0].data = 'R';
    tree.nodes[0].Parent = -1;
    tree.nodes[1].data = 'A';
    tree.nodes[1].Parent = 0;
    tree.nodes[2].data = 'B';
    tree.nodes[2].Parent = 0;
    tree.nodes[3].data = 'C';
    tree.nodes[3].Parent = 0;
    tree.nodes[4].data = 'D';
    tree.nodes[4].Parent = 1;
    tree.nodes[5].data = 'E';
    tree.nodes[5].Parent = 1;
    tree.nodes[6].data = 'F';
    tree.nodes[6].Parent = 3;
    tree.nodes[7].data = 'G';
    tree.nodes[7].Parent = 6;
    tree.nodes[8].data = 'H';
    tree.nodes[8].Parent = 6;
    tree.nodes[9].data = 'K';
    tree.nodes[9].Parent = 6;

打印一下：

    // 打印树结构
    printf("Index Data  Parent\n");
    for (int i = 0; i < tree.n; i++)
    {
        printf("%-5d %-5c %-5d\n", i, tree.nodes[i].data, tree.nodes[i].Parent);
    }

输出结果如下，和上图所示一致。

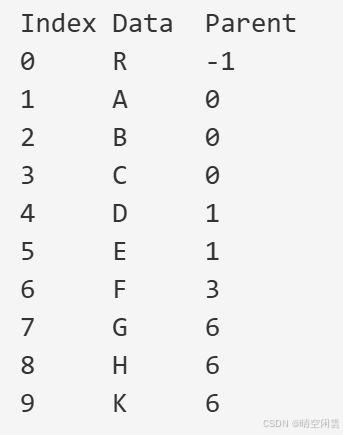
2. 孩子链表

把每个结点的孩子结点排列起来，看成是一个线性表，用单链表存储。

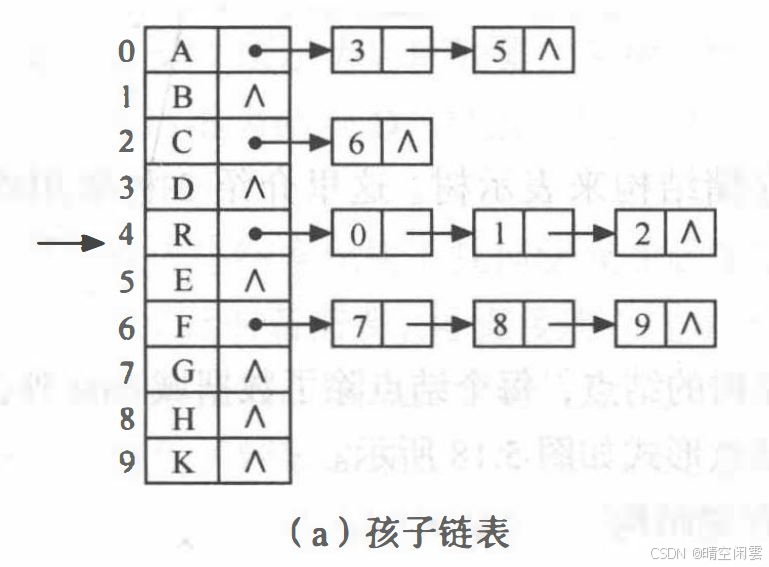
与双亲表示法相反， 孩子表示法便于查找孩子。因此可以把双亲表示法和孩子表示法结合起来，即将双亲表示和孩子链表合在一起。

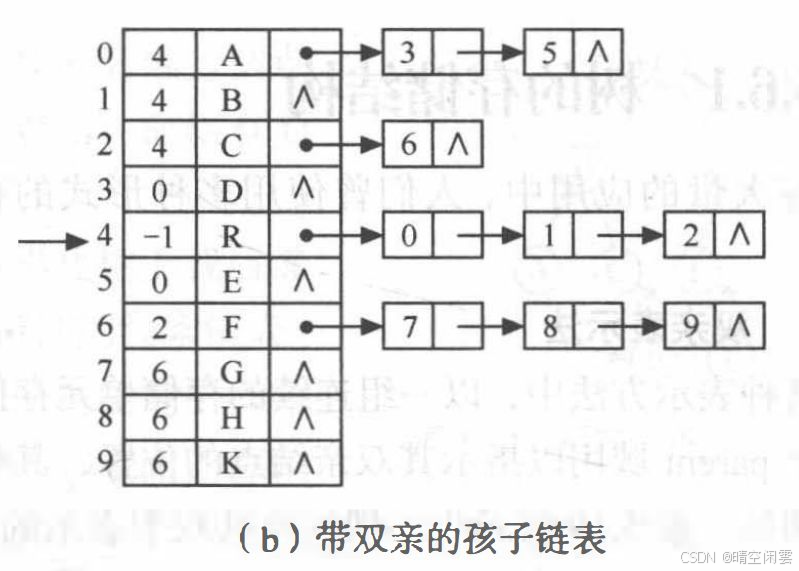
孩子链表结点：

// 孩子链表结点
typedef struct ChildNode
{
    int childIndex;         // 孩子结点的序号
    struct ChildNode *next; // 指向下一个结点
} ChildNode;

双亲+孩子链表结点：

typedef char TElemType;

// 双亲+孩子链表结点
typedef struct CTNode
{
    TElemType data;
    int Parent;
    ChildNode *child; // 孩子链表
} CTNode;

树结构：

// 树结构
#define MAX_TREE_SIZE 100
typedef struct
{
    CTNode nodes[MAX_TREE_SIZE];
    int r; // 根结点位置
    int n; // 结点数量
} CTree;

构造上面图片的树，代码较长，但是逻辑很简单。

	CTree tree;
    tree.n = 10;
    tree.r = 4; // 根结点R的位置

    // 初始化结点数据和双亲
    tree.nodes[0].data = 'A';
    tree.nodes[0].Parent = 4;
    tree.nodes[0].child = NULL;
    tree.nodes[1].data = 'B';
    tree.nodes[1].Parent = 4;
    tree.nodes[1].child = NULL;
    tree.nodes[2].data = 'C';
    tree.nodes[2].Parent = 4;
    tree.nodes[2].child = NULL;
    tree.nodes[3].data = 'D';
    tree.nodes[3].Parent = 0;
    tree.nodes[3].child = NULL;
    tree.nodes[4].data = 'R';
    tree.nodes[4].Parent = -1;
    tree.nodes[4].child = NULL;
    tree.nodes[5].data = 'E';
    tree.nodes[5].Parent = 0;
    tree.nodes[5].child = NULL;
    tree.nodes[6].data = 'F';
    tree.nodes[6].Parent = 2;
    tree.nodes[6].child = NULL;
    tree.nodes[7].data = 'G';
    tree.nodes[7].Parent = 6;
    tree.nodes[7].child = NULL;
    tree.nodes[8].data = 'H';
    tree.nodes[8].Parent = 6;
    tree.nodes[8].child = NULL;
    tree.nodes[9].data = 'K';
    tree.nodes[9].Parent = 6;
    tree.nodes[9].child = NULL;

    // 构建孩子链表
    // R的孩子: 0, 1, 2
    ChildNode *r_c0 = (ChildNode *)malloc(sizeof(ChildNode));
    ChildNode *r_c1 = (ChildNode *)malloc(sizeof(ChildNode));
    ChildNode *r_c2 = (ChildNode *)malloc(sizeof(ChildNode));
    r_c0->childIndex = 0;
    r_c0->next = r_c1;
    r_c1->childIndex = 1;
    r_c1->next = r_c2;
    r_c2->childIndex = 2;
    r_c2->next = NULL;
    tree.nodes[4].child = r_c0;

    // A的孩子: 3, 5
    ChildNode *a_c3 = (ChildNode *)malloc(sizeof(ChildNode));
    ChildNode *a_c5 = (ChildNode *)malloc(sizeof(ChildNode));
    a_c3->childIndex = 3;
    a_c3->next = a_c5;
    a_c5->childIndex = 5;
    a_c5->next = NULL;
    tree.nodes[0].child = a_c3;

    // C的孩子: 6
    ChildNode *c_c6 = (ChildNode *)malloc(sizeof(ChildNode));
    c_c6->childIndex = 6;
    c_c6->next = NULL;
    tree.nodes[2].child = c_c6;

    // F的孩子: 7, 8, 9
    ChildNode *f_c7 = (ChildNode *)malloc(sizeof(ChildNode));
    ChildNode *f_c8 = (ChildNode *)malloc(sizeof(ChildNode));
    ChildNode *f_c9 = (ChildNode *)malloc(sizeof(ChildNode));
    f_c7->childIndex = 7;
    f_c7->next = f_c8;
    f_c8->childIndex = 8;
    f_c8->next = f_c9;
    f_c9->childIndex = 9;
    f_c9->next = NULL;
    tree.nodes[6].child = f_c7;

打印：

// 打印树结构
printf("Index Data Parent Children\n");
for (int i = 0; i < tree.n; i++)
{
	printf("%-5d %-5c %-6d ", i, tree.nodes[i].data, tree.nodes[i].Parent);
	ChildNode *p = tree.nodes[i].child;
	while (p)
	{
		printf("%d ", p->childIndex);
		p = p->next;
	}
	printf("\n");
}

打印数据如下：

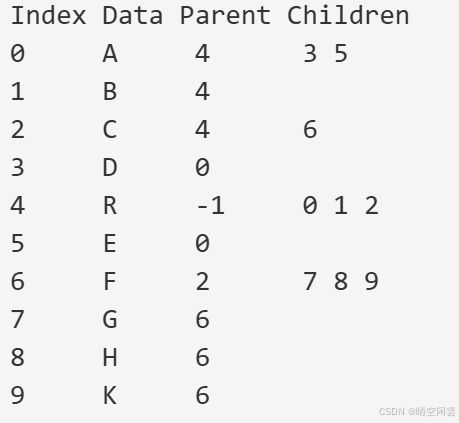
3. 孩子兄弟法（二叉树表示法）

用二又链表作树的存储结构，链表中每个结点的两个指针域分别指向其第一个孩子结点和下一个兄弟结点。

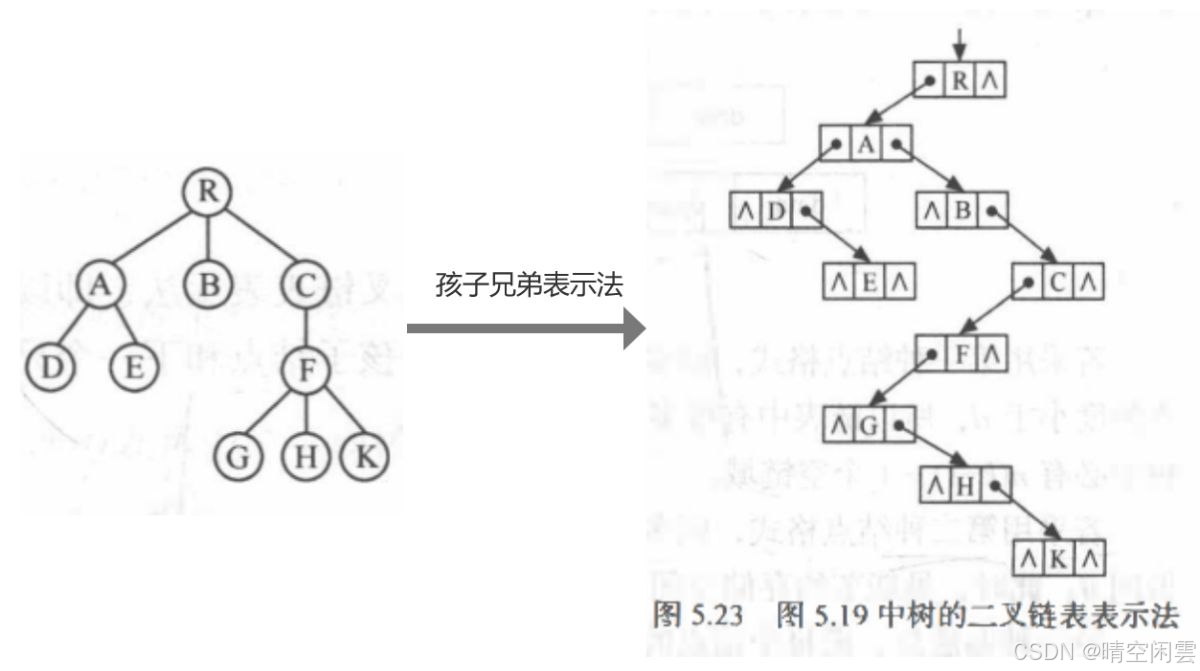
孩子兄弟结点结构：

typedef char TElemType;

// 孩子兄弟结点结构
typedef struct CSNode
{
    TElemType data;
    struct CSNode *firstchild, *nextsibling;
} CSNode, *CSTree;

为了方便构造上面图示的树，封装一个创建结点的方法：

// 创建结点
CSTree CreateNode(TElemType data)
{
    CSTree node = (CSTree)malloc(sizeof(CSNode));
    node->data = data;
    node->firstchild = NULL;
    node->nextsibling = NULL;
    return node;
}

构造出这棵树：

	// 构造树
    CSTree R = CreateNode('R');
    CSTree A = CreateNode('A');
    CSTree B = CreateNode('B');
    CSTree C = CreateNode('C');
    CSTree D = CreateNode('D');
    CSTree E = CreateNode('E');
    CSTree F = CreateNode('F');
    CSTree G = CreateNode('G');
    CSTree H = CreateNode('H');
    CSTree K = CreateNode('K');

    // 构建孩子兄弟关系
    R->firstchild = A;
    A->nextsibling = B;
    B->nextsibling = C;

    A->firstchild = D;
    D->nextsibling = E;

    C->firstchild = F;
    F->firstchild = G;
    G->nextsibling = H;
    H->nextsibling = K;

先序遍历进行打印：

// 简单先序遍历打印
void PreOrder(CSTree T)
{
    if (T)
    {
        printf("%c ", T->data);
        PreOrder(T->firstchild);
        PreOrder(T->nextsibling);
    }
}

调用：

    printf("先序遍历: ");
    PreOrder(R); // 打印：R A D E B C F G H K
    printf("\n");

这种存储结构的优点是它和二叉树的二叉链表表示完全一样， 便于将一般的树结构转换为二叉树进行处理， 利用二叉树的算法来实现对树的操作。因此孩子兄弟表示法是应用较为普遍的 一 种树的存储表示方法。

双亲表示法和孩子表示法是最直观的表示法，但实际上孩子兄弟法确实最常用的方法( ╯□╰ )。

4.5.2 树和二叉树的转换

1. 将树转换成二叉树

1. 加线：在兄弟之间加一连线；
2. 抹线：对每个结点，除了其左孩子外，去除其与其余孩子之间的关系；
3. 旋转：以树的根结点为轴心，将整树顺时针转45度。
   

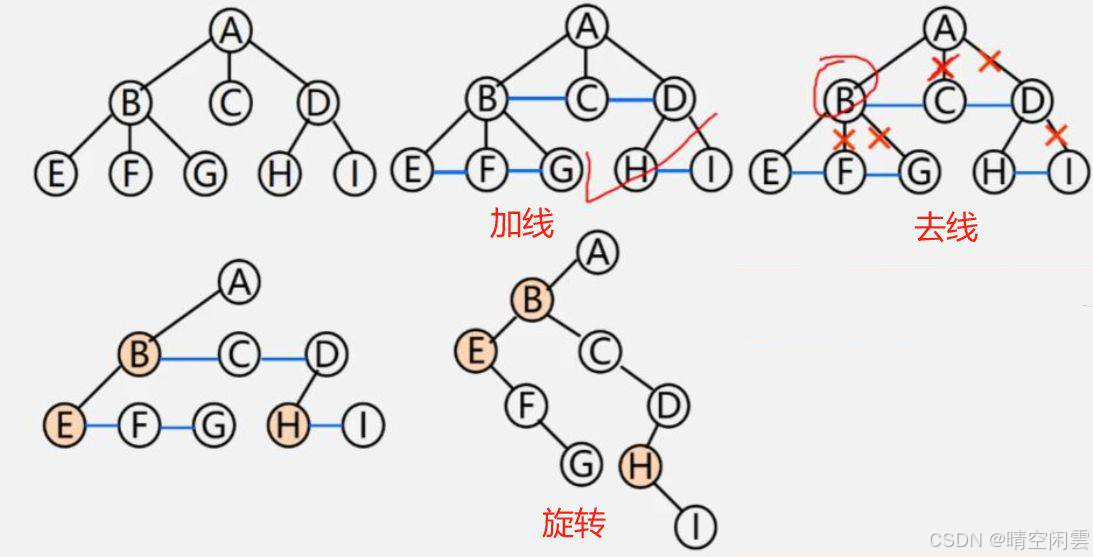
视频教程中提炼出一个口诀，容易记：兄弟相连留长子。至于代码实现，其实上面的孩子兄弟法就是这种二叉树的结构了。

2 将二叉树转换成树

1. 加线：若 p 结点是双亲结点的左孩子，则将 p 的右孩子，右孩子的右孩子……沿分支找到的所有右孩子，都与 p 的双亲用线连起来；
2. 抹线：抹掉原二叉树中双亲与右孩子之间的连线；
3. 调整：将结点按层次排列，形成树结构。

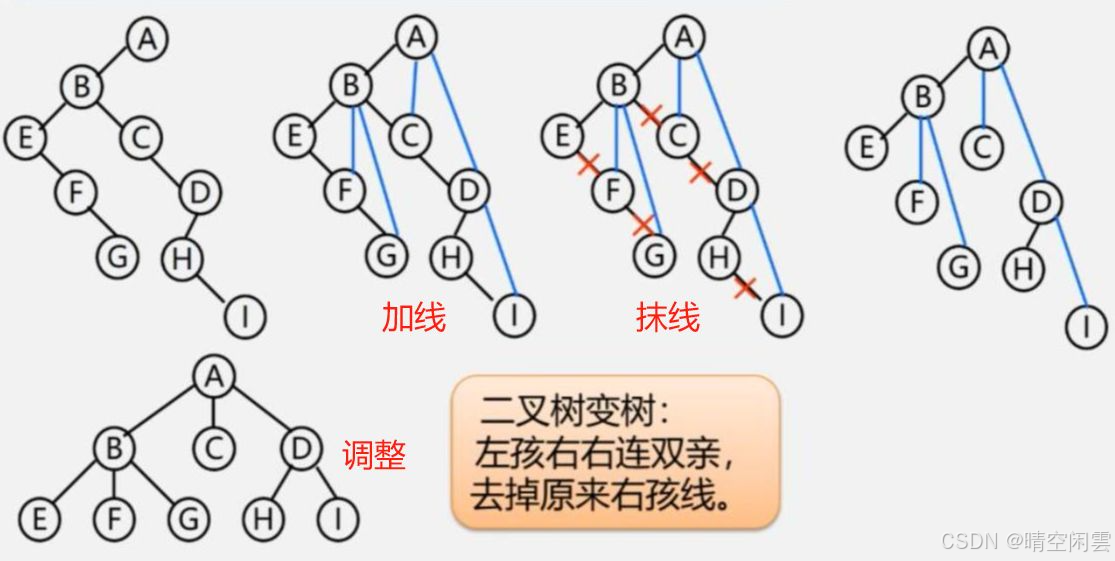
4.5.3 森林与二叉树的转换

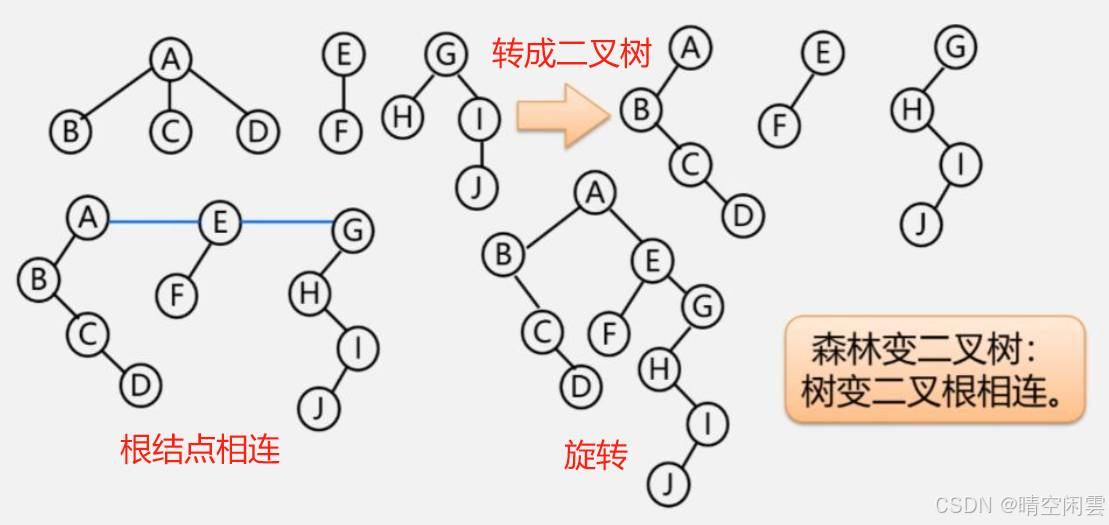
1. 森林转换成二叉树

1. 将各棵树分别转换成二叉树；
2. 将每棵树的根结点用线相连；
3. 以第一棵树根结点为二叉树的根，再以根结点为轴心，顺时针旋转构成二叉树型结构。
   

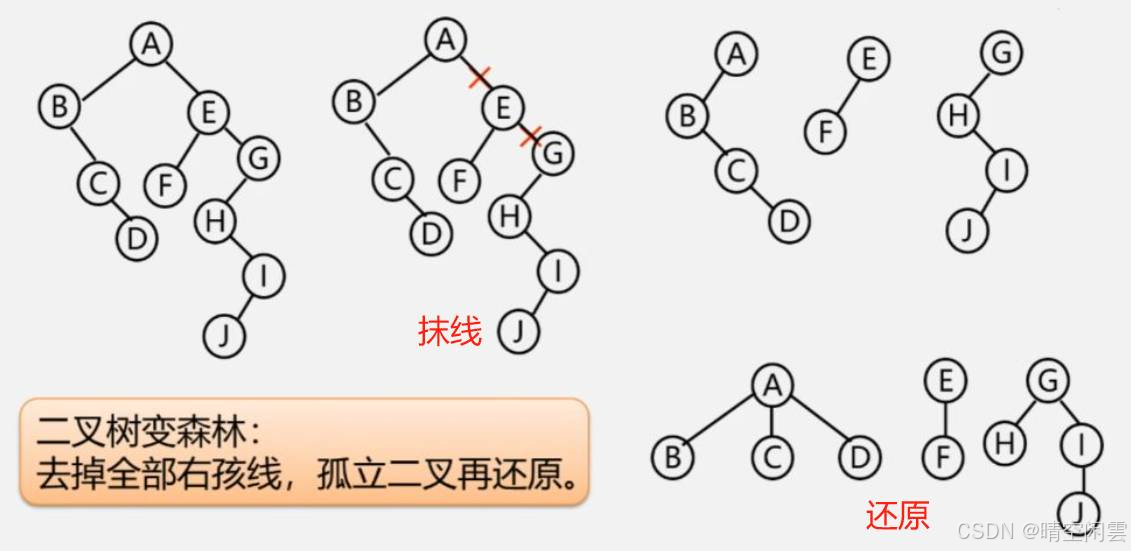
2. 二叉树转换成森林

1. 抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子间连线全部抹掉，使之变成孤立的二叉树；
2. 还原：将孤立的二又树还原成树。

4.5.4 树的遍历

分成3种方式：先序（先根）遍历、中序（后根）遍历和层次遍历。参考下图：

1. 先序（先根）遍历

【算法步骤】

在树的存储结构上，我使用了孩子兄弟法，因此如下步骤依据此结构进行。

若树非空，则从根节点开始：

1. 先访问树的根结点；
2. 递归遍历第一个孩子（即最左孩子）；
3. 递归遍历兄弟节点。

【代码实现】

因为存储结构使用了孩子兄弟法，代码和前面树的存储结构章节类似，不再赘述，遍历的思路和前面二叉树的思路非常类似。

// 树的先序遍历
void PreOrderTree(CSTree T)
{
    if (T)
    {
        printf("%c ", T->data);       // 访问根
        PreOrderTree(T->firstchild);  // 递归遍历孩子
        PreOrderTree(T->nextsibling); // 递归遍历兄弟
    }
}

【算法分析】

每个结点只访问一次，因此时间复杂度为 O(n)。

2. 中序（后根）遍历

【算法步骤】

若树非空，则从根节点开始：

1. 递归遍历第一个孩子（即最左孩子）；
2. 访问树的根结点；
3. 递归遍历兄弟节点。

【代码实现】

// 树的中序遍历
void InOrderTree(CSTree T)
{
    if (T)
    {
        // 先遍历第一个孩子
        InOrderTree(T->firstchild);
        // 访问根
        printf("%c ", T->data);
        // 再遍历兄弟（除第一个孩子外的其他孩子）
        InOrderTree(T->nextsibling);
    }
}

【算法分析】

每个结点只访问一次，因此时间复杂度为 O(n)。

**3. 层次遍历

【算法步骤】

核心思路是使用一个队列，将根结点、第一个孩子结点和第一个孩子的兄弟结点依次入队，从而实现层次遍历。

1. 根结点入队。
2. 队列不为空时，进行循环处理：从队头取出一个结点 p 进行访问。然后判断第一个孩子结点。
   1. 若第一个孩子结点不为空，则入队；
   2. 循环获取孩子的其他兄弟结点，若兄弟结点不为空，则入队；

【代码实现】

// 树的层次遍历
void LevelOrderTree(CSTree T)
{
    if (!T)
        return;
    // 简单队列实现
    CSTree queue[100];
    int front = 0, rear = 0;
    queue[rear++] = T;

    while (front < rear)
    {
        CSTree p = queue[front++];
        printf("%c ", p->data);

        // 依次入队所有孩子
        CSTree child = p->firstchild; // 第1个孩子
        while (child)
        {
            queue[rear++] = child;
            child = child->nextsibling; // 孩子的其他兄弟
        }
    }
}

【算法分析】

每个结点只访问一次，因此时间复杂度为 O(n)。空间复杂度方面，因为需要一个队列临时保存结点，但最多不会超过n，所以空间复杂度也是 O(n)。

4.5.5 森林的遍历

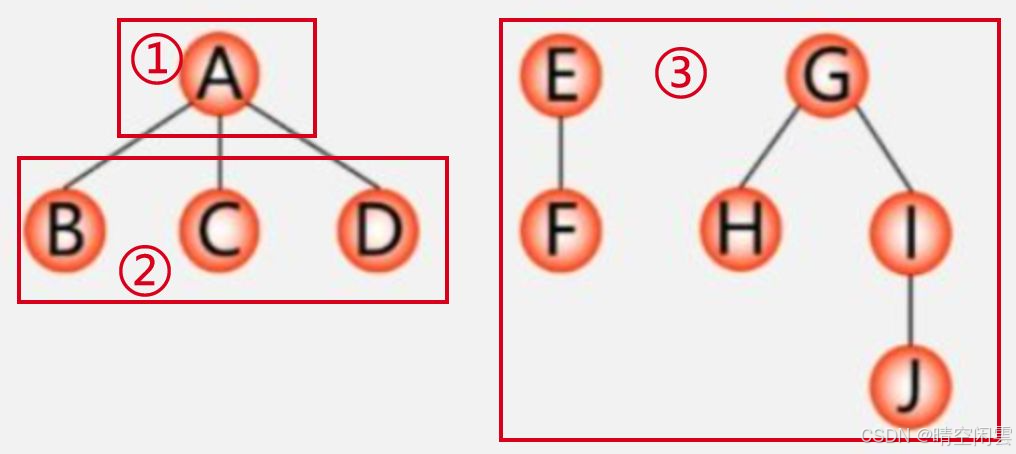
将森林看作由三部分构成：

1. 森林中第一棵树的根结点；
2. 森林中第一棵树的子树森林；
3. 森林中其它树构成的森林。

参考下图：

1. 先序遍历

【算法步骤】

若森林非空，则可按下述规则遍历：

1. 访问森林中第一棵树的根结点；
2. 先序遍历第一棵树的根结点的子树森林；
3. 先序遍历除去第一棵树之后剩余的树构成的森林。

其实本质上就是：依次从左至右对森林中的每一棵树进行先序遍历。

【代码实现】

// 先序遍历森林
void PreOrderForest(CSTree forest)
{
    CSTree p = forest;
    if (p)
    {
        printf("%c ", p->data);
        PreOrderForest(p->firstchild);
        PreOrderForest(p->nextsibling);
    }
}

【算法分析】

每个结点只访问一次，因此时间复杂度为 O(n)。

2. 中序遍历

【算法步骤】

若森林非空，则可按下述规则遍历：

1. 中序遍历第一棵树的根结点的子树森林；
2. 访问森林中第一棵树的根结点；
3. 中序遍历除去第一棵树之后剩余的树构成的森林。

其实本质上就是：依次从左至右对森林中的每一棵树进行中序遍历。

【代码实现】

// 中遍历森林
void InOrderForest(CSTree forest)
{
    CSTree p = forest;
    if (p)
    {
        InOrderForest(p->firstchild);
        printf("%c ", p->data);
        InOrderForest(p->nextsibling);
    }
}

【算法分析】

每个结点只访问一次，因此时间复杂度为 O(n)。