数据结构与算法-栈和队列-顺序栈（Sequence Stack）

2 栈和队列（Stack and Queue）

栈 (stack) 是限定仅在表尾进行插入或删除操作的线性表。栈来说，表尾端有其特殊含义，称为栈顶 (top)，相应地表头端称为栈底 (bottom)。不含元素的空表称为空栈。

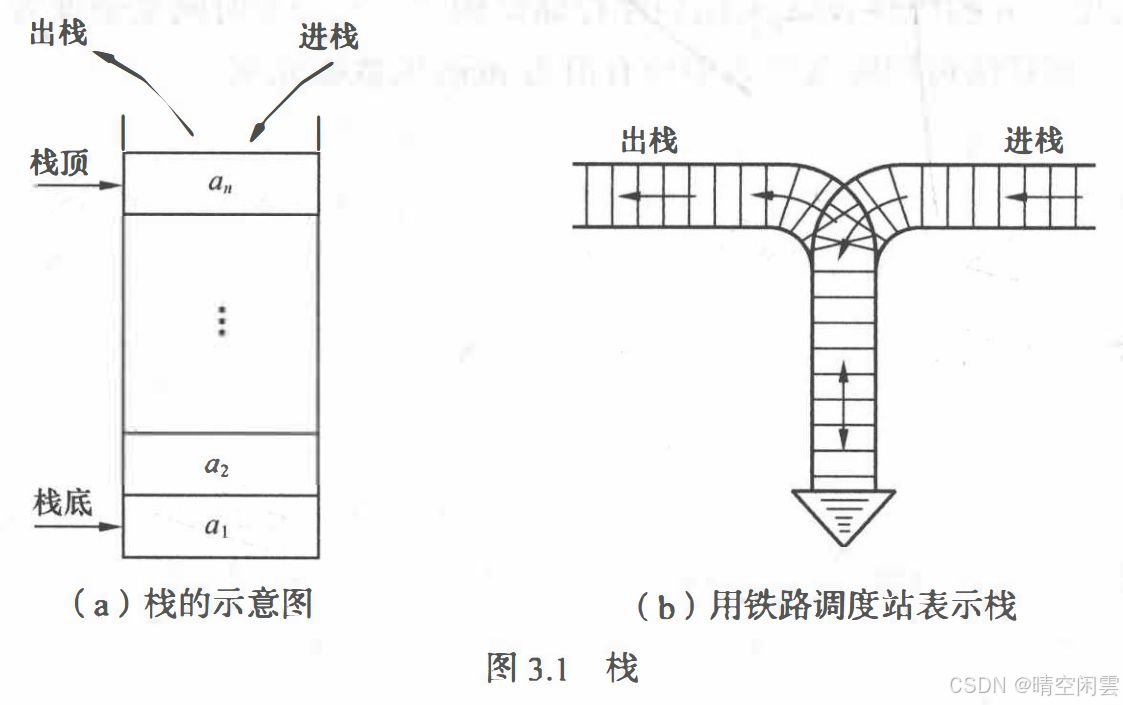
和栈相反，队列(queue)是一种先进先出(First I n First Out, FIFO)的线性表。它只允许在表的一端进行插入，而在另一端删除元素。

和线性表类似，栈也有两种存储表示方法，分别称为顺序栈和链栈。队列也有两种存储表示，顺序表示和链式表示。下面逐一用代码进行实现。

2.1 顺序栈（Sequence Stack）

书中顺序栈的基本操作有4个：初始化、入栈、出栈、获取栈顶元素，视频在此基础上增加了4个：销毁栈、判断栈是否为空、获取栈的大小、清空栈操作。我这里把8个都实现了。

同前面一样，有一些基础代码：

// 声明一些常量
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define TRUE 1
#define FALSE 0

// Status 是函数返回值类型， 其值是函数结果状态代码。
typedef int Status;
// Boolean 定义布尔型，值就是 TRUE 和 FALSE。
typedef int Boolean;

栈元素结构和栈结构：

#define MAXSIZE 100 // 顺序栈存储空间的初始分配量

// 栈元素类型定义
typedef struct
{
    int data; // 栈元素的数据
} SElemType;

// 顺序栈的结构体定义
typedef struct
{
    SElemType *top;
    SElemType *base; // 栈顶指针和栈底指针
    int stackSize;   // 栈的当前大小
} SqStack;

在编写代码过程中，经常需要查看栈内的内容，因此需要一个方法可以遍历栈，并打印其中的内容：

// 遍历栈
void TraverseStack(SqStack S)
{
    SElemType *p = S.base;
    while (p < S.top)
    {
        printf("%d ", p->data);
        p++;
    }
    printf("\n");
}

2.1.1 初始化

顺序栈的初始化操作就是为顺序栈动态分配一个预定义大小的数组空间。

【算法步骤】

1. 为顺序栈动态分配一个最大容量为 MAXSIZE 的数组空间，使 base 指向这段空间的基地址，即栈底。
2. 栈顶指针 top 初始为 base，表示栈为空。
3. stacksize 置为栈的最大容量 MAXSIZE。

【代码实现】

// 初始化栈
Status InitStack(SqStack *S)
{
    S->base = (SElemType *)malloc(MAXSIZE * sizeof(SElemType));
    if (!S->base) // 分配失败
        return OVERFLOW;
    S->top = S->base;       // 栈顶指针指向栈底
    S->stackSize = MAXSIZE; // 初始化栈大小
    return OK;
}

【算法分析】

需要提前分配一个 MAXSIZE 大小的空间。

2.1.2 入栈

入栈操作是指在栈顶插入一个新的元素。

【算法步骤】

1. 判断栈是否满，若满则返回 ERROR。
2. 将新元素压人栈顶，栈顶指针加1。

【代码实现】

// 入栈
Status Push(SqStack *S, SElemType e)
{
    if (S->top - S->base >= S->stackSize) // 栈满
        return ERROR;
    *(S->top) = e; // 将元素压入栈顶
    S->top++;      // 栈顶指针上移
    return OK;
}

2.1.3 出栈

出栈操作是将栈顶元素删除。

【算法步骤】

1. 判断栈是否空， 若空则返回ERROR。
2. 栈顶指针减1, 栈顶元素出栈。

【代码实现】

// 出栈
Status Pop(SqStack *S, SElemType *e)
{
    if (S->top == S->base) // 栈空
        return ERROR;
    S->top--;             // 栈顶指针下移
    *e = *(S->top);       // 将栈顶元素赋值给 e
    return OK;
}

2.1.4 获取栈顶元素

当栈非空时， 此操作返回当前栈顶元素的值， 栈顶指针保待不变。

【算法步骤】

1. 判断栈是否空， 若空则返回ERROR。
2. 栈顶指针减1, 栈顶元素出栈。

【代码实现】

// 获取栈顶元素
Status GetTop(SqStack S, SElemType *e)
{
    if (S.top == S.base) // 栈空
        return ERROR;
    *e = *(S.top - 1); // 获取栈顶元素
    return OK;
}

2.1.5 销毁栈

销毁栈就是将整个栈从内存中移除。清空栈只是移除栈内的元素，但是top和base指针都还在。

【算法步骤】

1. 检测栈是否已经分配了空间（base指针有值）。
2. 释放已分配的空间。
3. 将 base 和 top 指针置为 NULL。

【代码实现】

// 销毁栈
Status DestroyStack(SqStack *S)
{
    if (S->base) // 如果栈底指针不为空
    {
        // 因为栈元素并没有动态分配的内存，
        // 所以这里不需要遍历栈元素进行释放，我们只需要释放栈底指针所指向的内存。
        free(S->base); // 释放栈底指针所指向的内存
        S->base = NULL; // 将栈底指针置为 NULL
        S->top = NULL;  // 将栈顶指针置为 NULL
        S->stackSize = 0; // 栈大小置为 0
    }
    return OK;
}

2.1.6 判断栈是否为空

// 判断栈是否为空
Boolean IsEmpty(SqStack S)
{
    return S.top == S.base; // 如果栈顶指针等于栈底指针，则栈为空
}

2.1.7 获取栈的大小

// 获取栈的大小
int StackSize(SqStack S)
{
    return S.top - S.base; // 栈的大小等于栈顶指针和栈底指针的差值
}

2.1.8 清空栈操作

// 清空栈
Status ClearStack(SqStack *S)
{
    if (S->base) // 如果栈底指针不为空
    {
        S->top = S->base; // 将栈顶指针重置为栈底指针
        return OK;
    }
    return ERROR; // 栈已经为空
}