a的n次方优化

a的n次方优化

求a的n次方一般的最简单的方式就是从头乘到尾,但是这样子时间时间复杂度较高

       // 从头乘到尾 O(N)
        private static long pow0(int a,int n){
            long res = 1;
            for(int i=0;i<n;i++){
                res *= a;
            }
            return res;
        }

那我们应该如何优化呢？

方法一：

首先，我们是否可以使用二分法的思想，a的n次方等于a的n/2此方乘上a的n/2次方

然后，我们可以使用位移操作来加快代码执行速度，先设置一个参数ex，代表n从1到n/2的变化，

，再设置res为单前的结果，我们以自底向上的方式去执行代码，时间复杂度为logn

      //logn
      private static long pow(int a,int n){
            if (n==0) {
                return 1;
            }
            long res = a;//单前结果
            int ex = 1;//当前指数大小
            while((ex<<1)<=n){
                res = res * res;
                ex <<=1; //指数乘以2
            }
            return res*pow(a, n-ex);
        }

方法二：

我们使用了自底向上，那么我们也可以使用自顶向上的方法，我们可以判断n是偶数还是奇数，如果是偶数则等于其 (a,n) = （a,n/2) * (a,n/2) ，如果是奇数，则 (a,n) = (a,n/2) * (a,(a/2)+1), 这样子父问题就分解为子问题，使用递归求解

        private static long pow3(int a, int n){
            if(n==1){
                return a;
            }
            if(n%2==0){
                //偶数
                return pow3(a,n>>1)*pow3(a,n>>1);
            }
            else {
                //奇数
                return pow3(a,n>>1)*pow3(a,(n>>1)+1);

            }
        }

上面是不是可以再优化？

我们是不是可以把一些数据暂时存起开使用

        private static long pow2(int a, int n){
            if(n==1){
                return a;
            }

            if(n%2==0){
                  //偶数
                if(arr[n]!=0){
                    return arr[n];
                }
                arr[n] = pow2(a,n>>1)*pow2(a,n>>1); //将数据暂时存起来
                return arr[n];

            }
            else {
                //奇数
                if(arr[n]!=0){
                    return arr[n];
                }
                arr[n] =  pow2(a,n>>1)*pow2(a,(n>>1)+1); //将数据暂时存起来
                return arr[n];

            }
        }

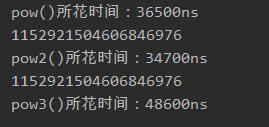
代码执行时间对比如下：