《商务与经济统计》（二）

第七章：抽样和抽样分布

1、如何从有限总体中抽取一个随机样本——方法：概率抽样。包括：简单随机抽样、分层随机抽样、整群抽样和系统抽样；从无限总体中抽样——要保证1)、每个个体来自同一总体2)、每个个体彼此独立。

2、利用收集的样本数据可以对总体参数进行点估计（样本统计量是总体相应量对应的一个点估计）。由于不同样本会给出不同点估计值，所以点估计量，比如“x拔（样本均值）”/“p拔（样本比率）”都是随机变量。他们的概率分布即为抽样分布。

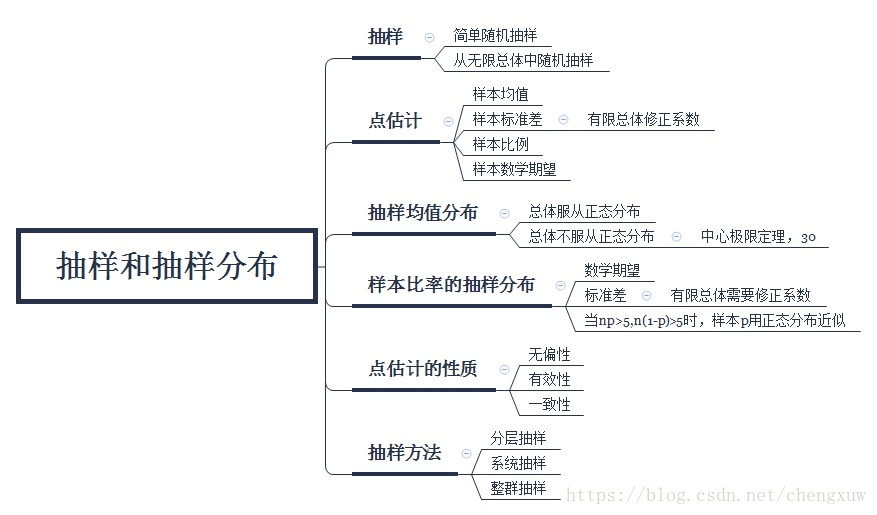
3、样本均值的抽样分布：数学期望=总体均值，标准差与总体是否有限有关（有限总体修正系数）。

但，样本均值的概率分布形式或者形态（确定其抽样分布特征的最后一步）取决于：

      1)、总体服从正态分布——样本均值也是正态分布

      2)、总体不服从正态分布——中心极限定理（样本容量n很大时，近似正态分布）帮助确定样本均值抽样分布的形状。

4、样本比率的抽样分布：数学期望=总体比率，标准差与总体是否有限有关（有限总体修正系数）。

5、点估计的性质：①、无偏性：样本统计量的期望=总体参数值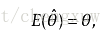②、有效性：标准误差更小的点估计量更有效；③、一致性。

 

第八章：区间估计

1、点估计量可能是也可能不是总体参数的好的估计，利用区间估计（点估计±边际误差）可以对估计的精确程度予以度量。

2、总体均值的区间估计：

①、总体标准差σ已知（利用历史数据or其他信息可以得到总体标准差σ的一个好的估计。极差除以4可作为标准差的估计。），给出置信水平，利用正态分布求边际误差。

                              

 

②、总体标准差σ未知，边际误差和总体均值的区间估计以t分布的概率分布为依据进行。

             

注意：如果总体服从正态分布，则以上置信区间是准确的，适用于任何样本容量；如果总体不服从正态分布，则该区间为近似（近似程度取决于总体的分布和样本容量）。一般的，样本容量≥30即可，若总体分布非正态但大致对称，n为15时即可得到较好的置信区间，若总体分布严重偏斜or包含异常点，需要n≥50。

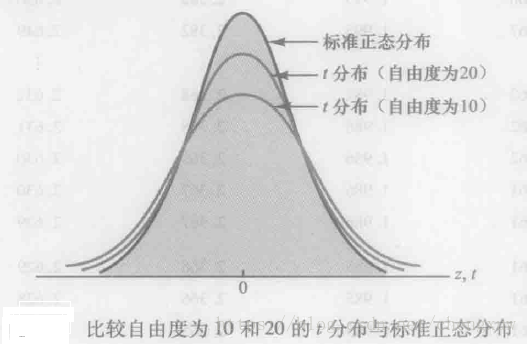
3、t分布：随着自由度的增大，t分布与标准正态分布之间的差别变小；

4、样本容量的确定：在给定置信水平下，利用求边际误差的公式可以求出所需的样本容量。

              

5、总体比率的区间估计与总体均值的区间估计方法类似。

 

第九章：假设检验（对总体均值和总体比率进行假设检验）

1、根据实际情况提出原假设和备择假设。

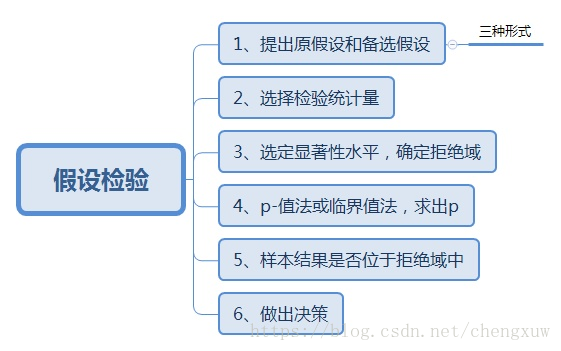
第一类错误：原假设H0为真却拒绝了H0；第二类错误：原假设H0为假时却接受了H0.

显著性水平α：是假设检验中的一个概念，是指当原假设为正确时人们却把它拒绝了的概率或风险（犯第一类错误的概率）。它是公认的小概率事件的概率值，必须在每一次统计检验之前确定，通常取α＝0.05或α＝0.01。这表明，当作出接受原假设的决定时，其正确的可能性（概率）为95％或99％。

单侧检验：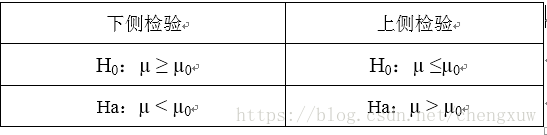

检验统计量：根据样本观测结果计算得到的，并据以对原假设和备择假设做出决策的某个样本统计量。检验统计量是用于假设检验计算的统计量，实际上是对总体参数的点估计量，但点估计量不能直接作为检验的统计量，只有将其标准化后，才能用于度量它与原假设的参数值之间的差异程度。

 

2、总体标准差σ已知，对总体均值进行假设检验（注：