Eigen求解LSCG问题

参考网址  https://blog.youkuaiyun.com/xuezhisdc/article/details/54634080

 

 

       Eigen中的求解Ax=b问题，应该采用什么方法， 才能较快的实现出来呢？ 主要结果是这样的：  

 

Eigen中有一些求解稀疏系数矩阵的线性方程组。由于稀疏矩阵的特殊的表示方式，因此获得较好的性能需要格外注意。查看《Eigen教程3 - 稀疏矩阵操作》，了解更多有关稀疏矩阵的内容。本文列出了Eigen中的稀疏求解器。同时也介绍了所有线性求解器的共同步骤。用户可以根据矩阵的性质，准确度的要求，来调整求解步骤，以提升代码的性能。注意：没有必要深入了解这些步骤后面隐藏的内容。

本文最后一部分列出了一个基准例程，可以用于窥探所有的求解器的性能。

稀疏求解器的列表

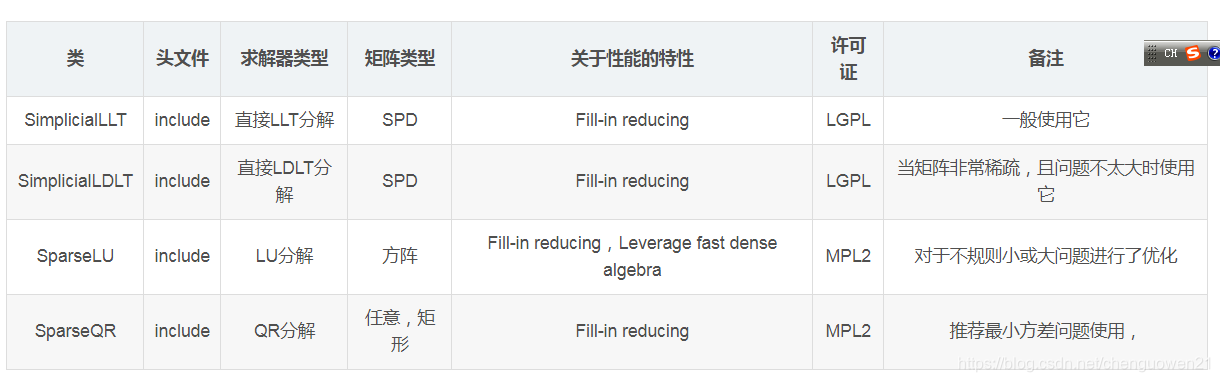
Eigen提供了一系列的内建求解器和封装了一些外部求解器库。

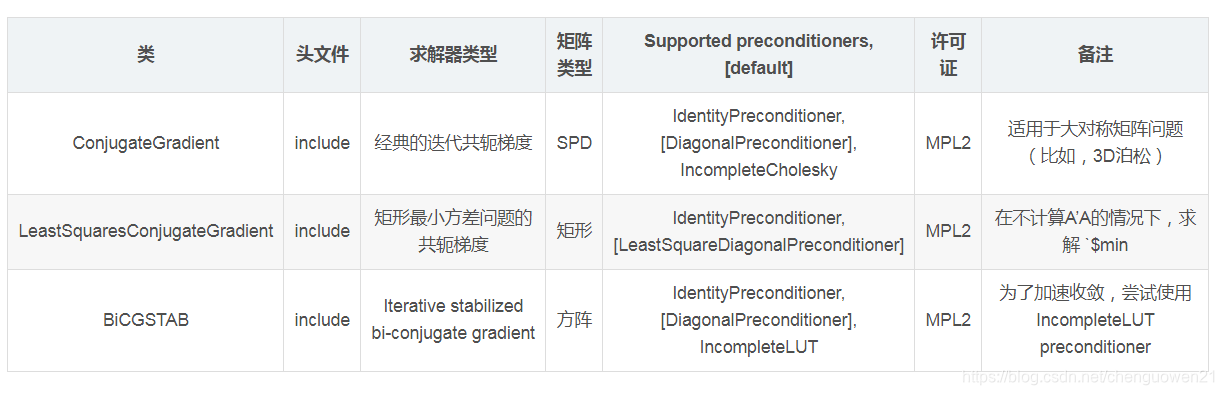
内建的直接求解器
* 说明：此处的SPD (symmetric positive definite) 表示对称正定。

 

 

用Auto最快 将Tolerance设置的大一些 是更好的。 

 

 

#include <Eigen/Sparse> //system solving and Eigen::SparseMatrix
#include <ctime>        //measure time to execute
#include <unsupported/Eigen/SparseExtra> //loadMarket

// Use typedefs instead of using if c++11 is not supported by your compiler
using SpMatrix = Eigen::SparseMatrix<double>;
using Matrix = Eigen::MatrixXd;

int main() {
  // Use multi-threading. If you don't have OpenMP on your system
  // it will simply use 1 thread and it will not crash. So do not worry about
  // that.
  Eigen::initParallel();
  Eigen::setNbThreads(6);

  // Load system matrices
  SpMatrix A, B;
  Eigen::loadMarket(A, "/home/iason/Desktop/Thesis/build/A.mtx");
  Eigen::loadMarket(B, "/home/iason/Desktop/Thesis/build/B.mtx");

  // Initialize the clock which will measure the solvers
  std::clock_t start;


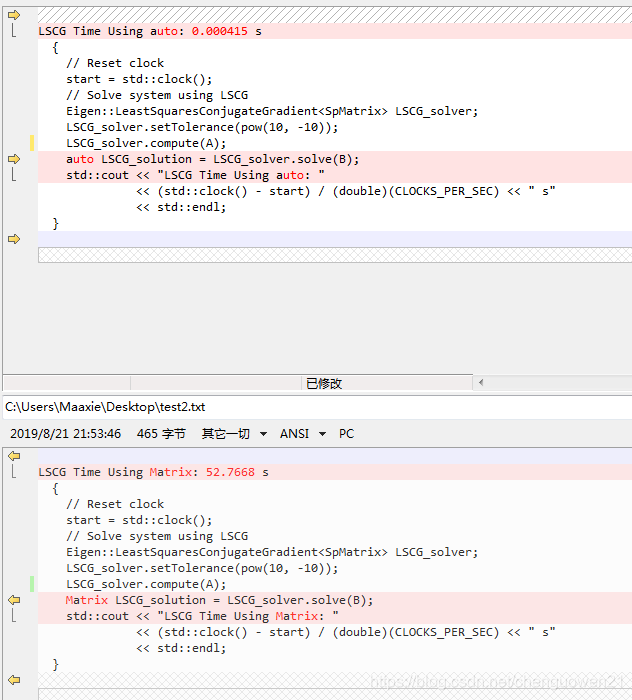
LSCG Time Using auto: 0.000415 s
  {
    // Reset clock
    start = std::clock();
    // Solve system using LSCG
    Eigen::LeastSquaresConjugateGradient<SpMatrix> LSCG_solver;
    LSCG_solver.setTolerance(pow(10, -10));
    LSCG_solver.compute(A);
    // Use auto specifier to hold the return value of solve. Eigen::Solve object
    // is being returned
    auto LSCG_solution = LSCG_solver.solve(B);
    std::cout << "LSCG Time Using auto: "
              << (std::clock() - start) / (double)(CLOCKS_PER_SEC) << " s"
              << std::endl;
  }





LSCG Time Using Matrix: 52.7668 s
  {
    // Reset clock
    start = std::clock();
    // Solve system using LSCG
    Eigen::LeastSquaresConjugateGradient<SpMatrix> LSCG_solver;
    LSCG_solver.setTolerance(pow(10, -10));
    LSCG_solver.compute(A);
    // Use Matrix specifier instead of auto. Implicit conversion taking place(?)
    Matrix LSCG_solution = LSCG_solver.solve(B);
    std::cout << "LSCG Time Using Matrix: "
              << (std::clock() - start) / (double)(CLOCKS_PER_SEC) << " s"
              << std::endl;
  }




SimplicialLDLT Time Using auto: 0.216593 s
  {
    // Reset clock
    start = std::clock();
    // Solve system using SimplicialLDLT
    Eigen::SimplicialLDLT<SpMatrix> SLDLT_solver;
    SLDLT_solver.compute(A.transpose() * A);
    auto SLDLT_solution = SLDLT_solver.solve(A.transpose() * B);

    std::cout << "SimplicialLDLT Time Using auto: "
              << (std::clock() - start) / (double)(CLOCKS_PER_SEC) << " s"
              << std::endl;
  }


SimplicialLDLT Time Using Matrix: 0.239976 s
  {
    // Reset clock
    start = std::clock();
    // Solve system using SimplicialLDLT
    Eigen::SimplicialLDLT<SpMatrix> SLDLT_solver;
    SLDLT_solver.compute(A.transpose() * A);
    // Use Matrix specifier instead of auto. Implicit conversion taking place(?)
    Matrix SLDLT_solution = SLDLT_solver.solve(A.transpose() * B);

    std::cout << "SimplicialLDLT Time Using Matrix: "
              << (std::clock() - start) / (double)(CLOCKS_PER_SEC) << " s"
              << std::endl;
  }
  return 0;

上述代码的运行时间分别为： 

LSCG Time Using auto : 0.000415 s

LSCG Time Using Matrix: 52.7668 s

SimplicialLDLT Time Using auto: 0.216593 s

SimplicialLDLT Time Using Matrix: 0.239976 s

As the results proove when I use Eigen::MatrixXd instead of auto I get the situation ggael described in one of his comments, namely LSCG not achieving a solution without setting a higher tolerance and SimplicialLDLT being much faster.

1. Are the solvers actually solving the system when I use auto?
2. Is the Solver object being implicitly converted to a Matrix Object when I use the Matrix specifier? Since When using LSCG the only change in the first two cases is the use of auto and Matrix respectively,does this implicit conversion to Matrix take 52.7668-0.000415 seconds?
3. Is there a faster way to extract the solution Matrix from the Solve object?

 

由于A'*A是对称正定，用LDLT的求解方法可以更快

Given the sparsity pattern of your matrix A, forming the normal equation explicitly and using a direct solver such as SimplicialLDLT will be much faster. Also better use a dense type for B since it is dense anyway and that internally, all solvers will convert the sparse right-hand-side to dense columns:

Eigen::MatrixXd dB = B; // or directly fill dB
Eigen::SimplicialLDLT<SpMatrix> solver;
solver.compute(A.transpose()*A);
MatrixXd x = solver.solve(A.transpose()*dB);

This takes 0.15s, in contrast to 6s for LSCG after the setting the tolerance of LSCG to 1E-14.