代码随想录训练营第三十六天| 1049. 最后一块石头的重量 II 494. 目标和 474.一和零-优快云博客

1049. 最后一块石头的重量 II

题目链接：

讲解链接：代码随想录

对01背包的巩固题思路要清晰

动规定义动态方程

找递推公式

初始化dp数组

确定一维dp的遍历顺序先顺着遍历物品再倒着遍历确保最大价值的物品被放入容量内不会导致漏值

递推一下公式试试看结果是否正确

这道题模拟了鸡蛋碰石头看最大重量是否大于等于其余重量进行相减得到题目所需

Java代码：

class Solution{
    public int lastStoneWeightII(int[] stones){
        int sum = 0;
        for(int i : stones){
            sum += i;
        }
        //其实只要找到该问题里 最大容量的最大价值 再用总数减去该最大价值
        //再用剩余的价值和他相减  而且因为 target是向下取整的 所以
        //sum - dp[target]一定大于等于 dp[target]
        //他给的题目描述就是一个模拟过程
        int target = sum >> 1;//位运算 除了2  防溢出
        //初始化dp数组
        int[] dp = new int[target + 1];
        for(int i = 0; i < stones.length; i++){
            //先遍历物品 再遍历物品价值 从后往前 依次遍历
            for(int j = target; j >= stones[i]; j--){
                //当前背包容量是否大于当前物品重量
                dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
                //比如说 1 2 2 3 dp[j - stones[i]] + stones[i] 假设背包容量为4
                // dp[j - stones[i]] + stones[i] = dp [4 - 3] + stones[3] = dp[1] + stones[3] = 4 
            } 
        }
        return sum - dp[target] - dp[target];
    }
}

494. 目标和

题目链接：494. 目标和 - 力扣（LeetCode）

讲解链接：代码随想录

有点难已经看不懂了但是顺着代码随想录思路还是能捋清楚不熟悉没见过

贴上代码随想录讲解

动态规划（一维dp数组）

将二维dp数组压缩成一维dp数组，我们在 01背包理论基础（滚动数组） (opens new window)讲过滚动数组，原理是一样的，即重复利用每一行的数值。

既然是重复利用每一行，就是将二维数组压缩成一行。

dp[i][j] 去掉行的维度，即 dp[j]，表示：填满j（包括j）这么大容积的包，有dp[j]种方法。

确定递推公式

二维DP数组递推公式： dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];

去掉维度i 之后，递推公式：dp[j] = dp[j] + dp[j - nums[i]] ，即：dp[j] += dp[j - nums[i]]

这个公式在后面在讲解背包解决排列组合问题的时候还会用到！

dp数组如何初始化

在上面二维dp数组中，我们讲解过 dp[0][0] 初始为1，这里dp[0] 同样初始为1 ,即装满背包为0的方法有一种，放0件物品。

确定遍历顺序

在动态规划：关于01背包问题，你该了解这些！（滚动数组） (opens new window)中，我们系统讲过对于01背包问题一维dp的遍历。

遍历物品放在外循环，遍历背包在内循环，且内循环倒序（为了保证物品只使用一次）。

举例推导dp数组

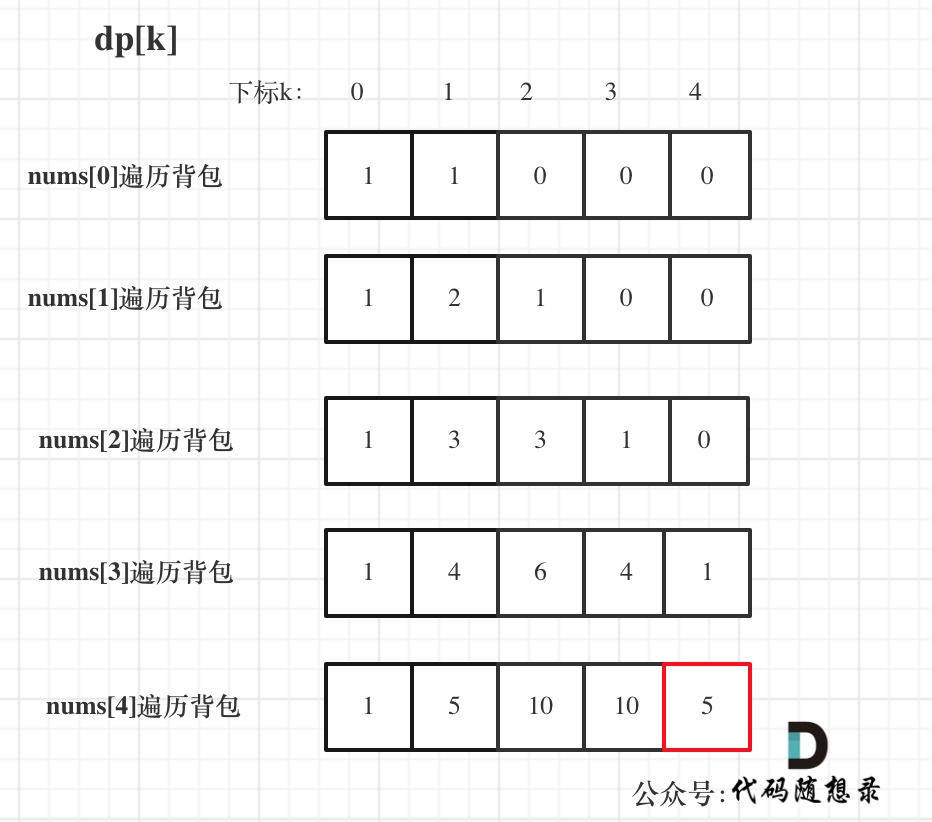
输入：nums: [1, 1, 1, 1, 1], target: 3

bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

Java代码：

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) sum += nums[i];

        //如果target的绝对值大于sum，那么是没有方案的
        if (Math.abs(target) > sum) return 0;
        //如果(target+sum)除以2的余数不为0，也是没有方案的
        if ((target + sum) % 2 == 1) return 0;

        int bagSize = (target + sum) / 2;
        int[] dp = new int[bagSize + 1];
        dp[0] = 1;

        for (int i = 0; i < nums.length; i++) {
            for (int j = bagSize; j >= nums[i]; j--) {
                dp[j] += dp[j - nums[i]];
            }
        }

        return dp[bagSize];
    }
}

474.一和零

题目链接：474. 一和零 - 力扣（LeetCode）

讲解链接：代码随想录

状态好差太困了看不懂了

多维度01背包

Java代码：

//给定背包容量 装满背包最多有多少个物品
class Solution{
    public int findMaxForm(String[] strs, int m, int n){
        //dp[i][j] 表示 i个0 j个1 的最大子集
        int[][] dp = new int[m + 1][n + 1];
        int onenum, zeronum;
        for(String str : strs){
            onenum = 0;
            zeronum = 0;
            for(char ch : str.toCharArray()){
                if(ch == '0'){
                    zeronum++;
                } else {
                    onenum++;
                }
            }
            //倒序遍历
            for(int i = m; i >= zeronum; i--){
                for(int j = n; j >= onenum; j--){
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeronum][j - onenum] + 1);
                }
            }
        }//有几种办法把当前容量为m n的背包装满 不同维度的01背包
        //看不懂了 状态太差 好困
        return dp[m][n];
    }
}

day 35 打卡