回顾transformer中绝对位置编码(absolute position embedding)
在transformer的实现中,所有的input tokens是无序的,是没法像RNN的方法一样学到token之间的位置顺序关系,但是自然语言一定是有语序在里面的,所以原始的transformer的代码实现里就提供了一种非常简单的位置编码,输入的是一个和max_sequence_length一样长的固定index序列,比如在max_sequence_length=64的情况下,输入的位置信息序列就是[0,1,2,3…62,63],然后通过一个embedding层让网络自己去学习位置的编码和表征。因为不管输入的文本是什么,位置编码永远是一个定值的序列(在不同的网络中仅长度会变化),所以这就是一种绝对位置编码方式。我个人对这种位置编码方式是否能提供有用的位置信息是存疑的,因为当网络训练好了以后,所有的input embedding相当于都加上一个定值,然而不同的input里面的位置和语义信息都是不同的,我认为这种加定值的方式并不能学到一些位置带来的语义上的差别,但毕竟增加了一定的参数量,可能聊胜于无吧。
贴一下transformer中绝对位置编码的实现,在modeling_bert.py中,实现也很简单:
class BertEmbeddings(nn.Module):
def __init__(self, config):
super().__init__()
self.word_embeddings = nn.Embedding(config.vocab_size, config.hidden_size, padding_idx=config.pad_token_id)
self.position_embeddings = nn.Embedding(config.max_position_embeddings, config.hidden_size) #初始化定义position_embedding的embedding层,其实底层就是一个fc
self.token_type_embeddings = nn.Embedding(config.type_vocab_size, config.hidden_size)
def forward(self, input_ids=None, token_type_ids=None, position_ids=None, inputs_embeds=None):
if input_ids is not None:
input_shape = input_ids.size()
else:
input_shape = inputs_embeds.size()[:-1]
seq_length = input_shape[1]
if position_ids is None:
position_ids = self.position_ids[:, :seq_length] #生成定值的序列
if position_ids.dtype is not torch.long:
position_ids = position_ids.to(torch.long)
if token_type_ids is None:
token_type_ids = torch.zeros(input_shape, dtype=torch.long, device=self.position_ids.device)
if inputs_embeds is None:
inputs_embeds = self.word_embeddings(input_ids)
embeddings = inputs_embeds
embeddings += token_type_embeddings
if self.position_embedding_type == "absolute":
position_embeddings = self.position_embeddings(position_ids) #输入的固定序列经过一个fc得到位置编码,直接point-wise加回到token embedding上
embeddings += position_embeddings
embeddings = self.LayerNorm(embeddings)
embeddings = self.dropout(embeddings)
return embeddings
相对位置编码方法详解和公式推导
相对位置编码的方法主要是出自于Google的一篇paper《Self-Attention with Relative Position Representations》
先说一下transformer中的self-attention机制:
每一层transformer由h个attention heads组成,其中每个attention head的输入为n个元素组成的token序列
x
=
(
x
1
,
.
.
.
,
x
n
)
x = (x_1,...,x_n)
x=(x1,...,xn), 经过self-attention的处理后,输出为同样长度的序列
z
=
(
z
1
,
.
.
.
z
n
)
z = (z_1,...z_n)
z=(z1,...zn)。 其中,输出序列的每个token
z
i
z_i
zi的计算过程为:
z
i
=
∑
j
=
1
n
α
i
j
(
x
j
W
V
)
z_i = \sum^n_{j=1}\alpha_{ij}(x_jW^V)
zi=j=1∑nαij(xjWV)
其中
W
V
W^V
WV为网络要学习的参数,就是query,key,value中的value所对应的fc层。
其中权重系数
α
i
j
\alpha_{ij}
αij通过softmax函数计算得到:
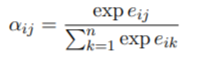
其中
e
i
j
e_{ij}
eij就是通过query和key计算得到的:
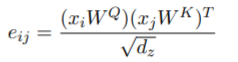
其中
W
Q
W^Q
WQ和
W
K
W^K
WK 是另外两个要学习的参数矩阵,就是query和key对应的fc层。除以
d
z
d_z
dz开根号是为了归一化。最后把h个attention heads各自self-attention之后的结果concat到一起,然后经过fc层combine到一起就经过了一层transformer的处理。通常一个transformer里包含很多这样的层,每一层都在学习不同的
W
Q
W^Q
WQ、
W
K
W^K
WK、
W
V
W^V
WV。
了解了transformer中的self-attention之后,就要在这个过程中加入位置关系的表征,考虑token间这种pairwise的位置关系,也就是变成relation-aware的self-attention。
假如我们用
a
i
j
a_{ij}
aij来表示两个token之间的相对位置关系(注意这里是
a
i
j
a_{ij}
aij不是
α
i
j
\alpha_{ij}
αij啦),只要在上述self-attention的计算过程中把位置关系的表征
a
i
j
a_{ij}
aij加进去就行了,由于Query是查询词,只需要在key和value中引入相对位置关系表征就可以,所以
a
i
j
a_{ij}
aij有两个vector,分别表示为
a
i
j
V
a^V_{ij}
aijV和
a
K
i
j
a^K{ij}
aKij,然后对应self-attention,每一步的公式就变为:
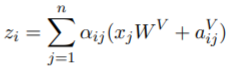
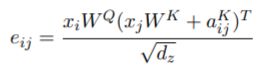
那么相对位置关系表征
a
i
j
a_{ij}
aij是怎么得到的呢?
其实实现很简单,就是算了每个token之间的相对距离,然后通过一个embedding层的学习将相对距离转化为相对位置的embedding。用公示来表示就是:
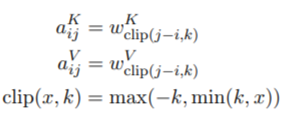
其中限制了相对距离的最大值,也就是当两个token之间的相对距离超过k了以后,就全都置为k,作者认为相对位置信息在一定距离外就没有太大作用了,而且这样可以使模型泛化到训练期间看不到的序列长度。
截了一张论文中的图来表示这个算相对距离的过程:

总结来说,这篇文章的主要方法就是表征了token之间的相对位置关系,并且在每一层transformer的self-attention中都加入这种相对位置信息,可以使得模型在学习的过程中持续考虑位置关系的影响,并且针对不同的输入序列可以泛化出对于其中包含的不同位置信息的捕捉,使得transformer能够更好的建模语句中包含的语义信息。
相对位置编码代码实现
现在hugging face里其实已经整合了相对位置编码方法的code,可以通过更改config来使用。
主要修改在modeling_bert.py的BertSelfAttention()类中:
class BertSelfAttention(nn.Module):
def __init__(self, config):
super().__init__()
self.position_embedding_type = getattr(config, "position_embedding_type", "absolute")
if self.position_embedding_type == "relative_key" or self.position_embedding_type == "relative_key_query":
self.max_position_embeddings = config.max_position_embeddings
self.distance_embedding = nn.Embedding(2 * config.max_position_embeddings - 1, self.attention_head_size) #这里就是公式里的2k-1
def forward(
self,
hidden_states,
attention_mask=None,
head_mask=None,
encoder_hidden_states=None,
encoder_attention_mask=None,
output_attentions=False,
token_type_ids = None
):
mixed_query_layer = self.query(hidden_states)
# If this is instantiated as a cross-attention module, the keys
# and values come from an encoder; the attention mask needs to be
# such that the encoder's padding tokens are not attended to.
if encoder_hidden_states is not None:
mixed_key_layer = self.key(encoder_hidden_states)
mixed_value_layer = self.value(encoder_hidden_states)
attention_mask = encoder_attention_mask
else:
mixed_key_layer = self.key(hidden_states)
mixed_value_layer = self.value(hidden_states)
query_layer = self.transpose_for_scores(mixed_query_layer)
key_layer = self.transpose_for_scores(mixed_key_layer)
value_layer = self.transpose_for_scores(mixed_value_layer)
# Take the dot product between "query" and "key" to get the raw attention scores.
attention_scores = torch.matmul(query_layer, key_layer.transpose(-1, -2))
if self.position_embedding_type == "relative_key" or self.position_embedding_type == "relative_key_query":
seq_length = hidden_states.size()[1]
position_ids_l = torch.arange(seq_length, dtype=torch.long, device=hidden_states.device).view(-1, 1)#生成[0,...,seq_length]的矩阵,生成两个相减就可以得到两两token之间的相对距离矩阵
position_ids_r = torch.arange(seq_length, dtype=torch.long, device=hidden_states.device).view(1, -1)
distance = position_ids_l - position_ids_r
positional_embedding = self.distance_embedding(distance + self.max_position_embeddings - 1) #都变成非负整数
positional_embedding = positional_embedding.to(dtype=query_layer.dtype) # fp16 compatibility
if self.position_embedding_type == "relative_key":
relative_position_scores = torch.einsum("bhld,lrd->bhlr", query_layer, positional_embedding) #[贴一个einsum的详解](https://blog.youkuaiyun.com/a2806005024/article/details/96462827)
attention_scores = attention_scores + relative_position_scores
elif self.position_embedding_type == "relative_key_query":
relative_position_scores_query = torch.einsum("bhld,lrd->bhlr", query_layer, positional_embedding)
relative_position_scores_key = torch.einsum("bhrd,lrd->bhlr", key_layer, positional_embedding)
attention_scores = attention_scores + relative_position_scores_query + relative_position_scores_key
论文中的结果我就不贴了,我有在自己的task上加这个方法,当我的model比较大的时候,通常都需要有initial weights,但是这种方法由于在每层transformer中都引入了新的参数,所以引入后会破坏原来public model的参数,而且加入了relative position embedding的public model我也没有找到,所以对于需要initial weights的大model效果都不是很好,没有提升。但是当我train 小model的时候,比如2~3层的transformer,这种一般没有initial weights也可以train的很好,所以当我的小model随机初始化的时候,加上这种方法效果确实是有提升的。





 本文介绍了Transformer中相对位置编码的概念,相对于绝对位置编码,它考虑了token间的相对距离,通过在self-attention计算中加入相对位置信息的表示,增强了模型对语序的捕获能力。文中详细解释了相对位置编码的公式推导,并提到在实际代码实现中,Hugging Face的库已支持该方法,但在大型模型中可能因引入额外参数而影响预训练权重的使用。
本文介绍了Transformer中相对位置编码的概念,相对于绝对位置编码,它考虑了token间的相对距离,通过在self-attention计算中加入相对位置信息的表示,增强了模型对语序的捕获能力。文中详细解释了相对位置编码的公式推导,并提到在实际代码实现中,Hugging Face的库已支持该方法,但在大型模型中可能因引入额外参数而影响预训练权重的使用。

















 1352
1352

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










