MATLAB-偶次非球面曲线拟合
于 2024-01-25 14:48:15 首次发布
 本文介绍了偶次非球面的特性,重点讲解了如何通过矢高公式获取离散点数据后进行曲线拟合,以求解k、c和偶次非球面系数。给出了非线性拟合的代码示例,展示了使用lsqcurvefit函数进行参数估计的过程和结果图形。
本文介绍了偶次非球面的特性,重点讲解了如何通过矢高公式获取离散点数据后进行曲线拟合,以求解k、c和偶次非球面系数。给出了非线性拟合的代码示例,展示了使用lsqcurvefit函数进行参数估计的过程和结果图形。
该文章已生成可运行项目,
本文章已经生成可运行项目





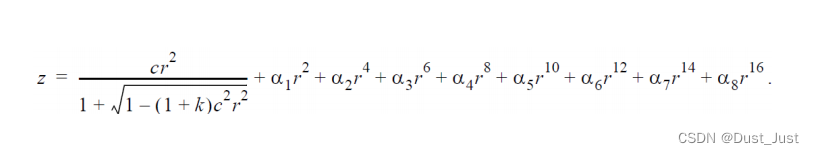 以下为某偶次非球面截面矢高图。
以下为某偶次非球面截面矢高图。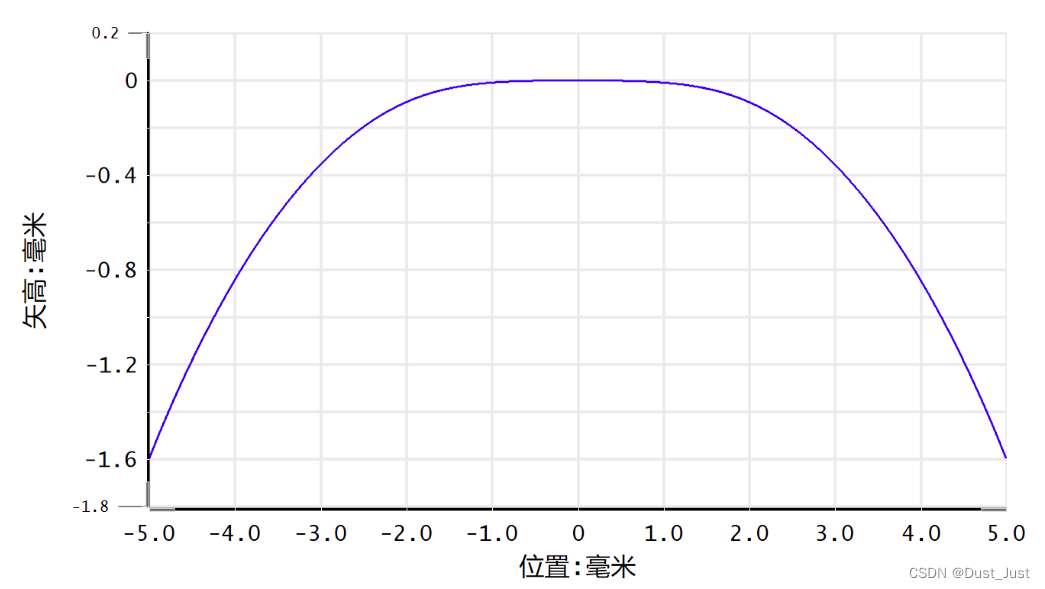 在已知离散点的情况下,我们相当于已知z和r的对应关系,需要得到的是k、c、ai的值。
在已知离散点的情况下,我们相当于已知z和r的对应关系,需要得到的是k、c、ai的值。 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 132
132

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








