从相控阵天线波束指向角到移相器相位:一维与二维相控阵天线控制算法简介
我们前面的文章卫星通信之相控阵天线-极简版中介绍了相控阵天线的基本组成和工作原理。
相控阵天线由数十至数千个天线阵元组成,阵元间距固定,通常为半波长。通过为每个阵元配备一个移相器,我们可以调节各阵元接收或发射信号的相位,使信号在空间特定方向实现同相叠加,从而获得增益放大,并将天线波束对准卫星。
我们在机载相控阵天线控制器设计 一文中已经详细介绍了相控阵天线控制器的逻辑。
天线控制器综合卫星位置、天线平台位置及姿态数据,计算出卫星信号相对于天线平台的入射角,即相控阵天线的波束指向角。随后,天线控制器将计算得到的天线波束指向角,方位角,俯仰角(离轴角)和极化角,输出给相控阵天线。相控阵天线内部的逻辑控制单元则根据这些角度,控制天线阵列形成对准卫星的波束。
相控阵天线控制器的总体逻辑关系如下图所示。
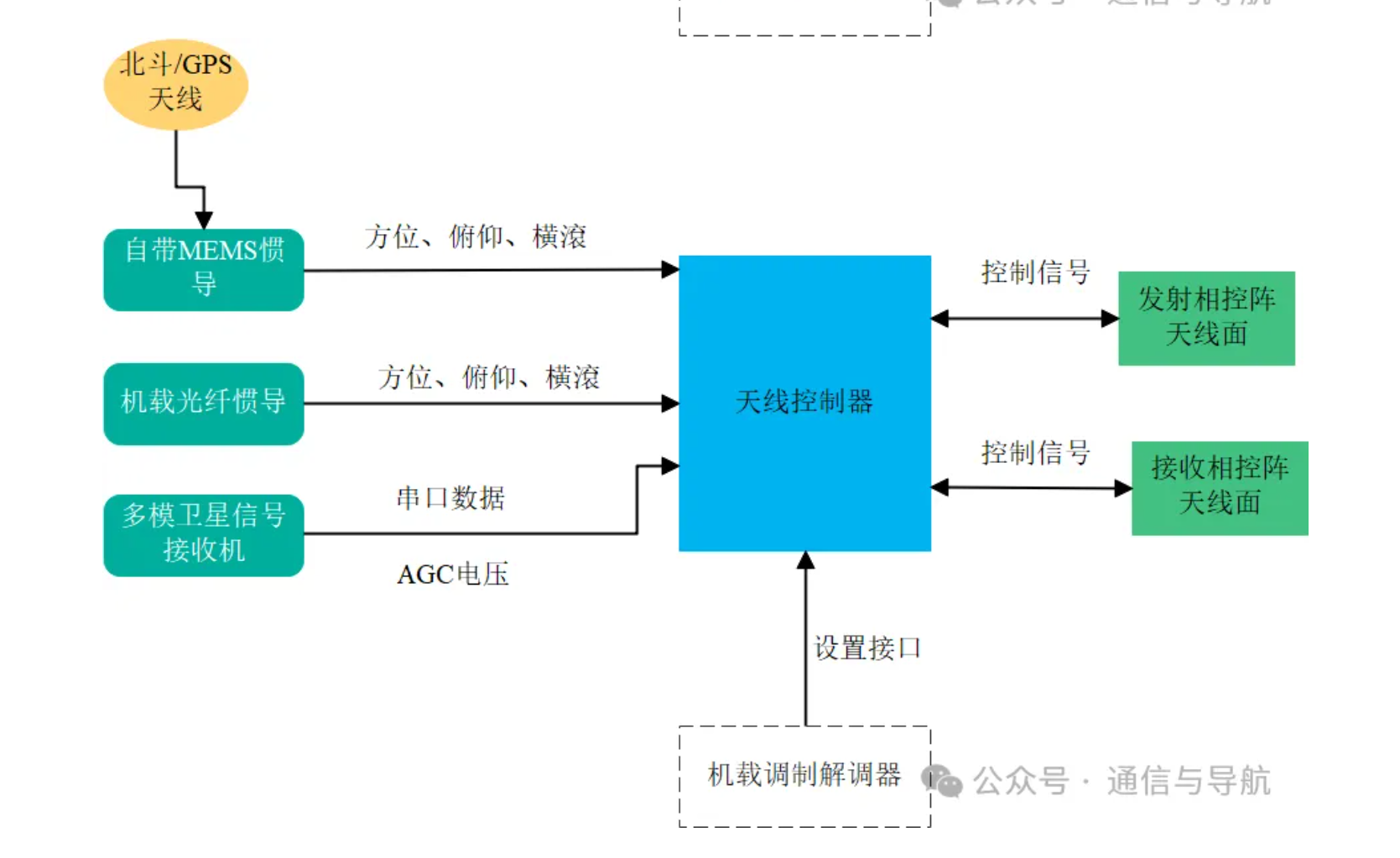
那么,今天我们就提出一个核心问题,**天线控制器算出了波束指向角,相控阵天线内部到底是咋把这个角度变成每一个移相器的具体数值的。**这正是本文要解答的核心问题。
1.相控阵天线的内部组成
1.1 内部组成
在计算移相器的相位之前,我们需要先明确移相器在系统中的位置。一个标准的相控阵天线,尤其是在卫星通信中常用的类型,通常由辐射层,幅相控制层,馈电与分配层,逻辑控制和电源层这四个层次构成。
以一个128阵元的天线为例,
① 辐射层
这是天线的最外层,即最外面的天线阵子。
- 组成,由大量按规则排列,例如 16 × 8 16 \times 8 16×8,的阵元组成。常见形式包括贴片天线,偶极子天线或喇叭天线。我们通常将阵元间距固定在半波长 λ 2 \frac{\lambda}{2} 2λ 左右,以防止产生栅瓣。
- 功能,负责将电信号辐射至空间,或将空间中的电磁波接收转换为电信号。
② 幅相控制层
幅相控制层,这是实现波束赋形的关键。
- 组成,主要由多颗 波束赋形芯片, BFIC, 组成。每颗芯片可能控制4个,8个甚至16个通道。每颗BFIC内部集成了,
- 移相器, Phase Shifter, 用于改变信号相位。
- 可变增益放大器, VGA, 用于调整信号幅度。
- 收发切换开关, T/R Switch, 用于切换发射和接收模式。
③ 馈电与分配网络
- 组成,包括功分器和合路器。
- 功能,在发射时,将一路射频信号等分为128路并送至各BFIC,在接收时,将128路信号汇聚成一路送往后端处理。
④ 逻辑控制与电源层
- 组成,FPGA/MCU,二次电源模块。
- 功能,负责与外部天线控制器通信,接收波束指向指令,通过查表等方式生成128组幅相控制码字,并通过串行总线,如SPI,快速配置各个BFIC。
1.2 信号流向
为直观理解,我们以发射模式为例描述信号连接关系。
- 信号源输入,调制解调器输出端连接上变频器,将信号上变频至Ku/Ka频段,然后输入相控阵天线。
- 一级/多级分配,信号进入馈电网络,通过树状结构的功分器,从1路逐级分配为2路,4路……直到128路。
- 幅相调整,这128路信号分别进入各个BFIC的对应通道。在BFIC内部,信号首先经过VGA调整幅度,再经过移相器调整相位,此相位即根据波束指向角计算得到的理论值。
- 末级放大,调整后的信号经过功率放大器,PA,提升发射能量。
- 辐射输出,最后通过射频走线连接到对应的天线阵元,128个阵元在空间中的辐射信号通过干涉叠加,最终形成具有特定指向的波束。
2.一维相控阵天线的移相器相位计算
为便于理解,我们先以一维线阵为例进行分析。
场景设定
- 工作频率 f f f, 12.5 GHz 12.5\,\text{GHz} 12.5GHz,典型的 Ku 频段下行频率。
- 阵列规模, 1 × 8 1 \times 8 1×8 阵列,8个天线阵元排成一排。
- 阵元间距 d d d, 半个波长。
- 期望波束指向角 θ \theta θ, 40 ∘ 40^\circ 40∘,离轴角。
第一步,计算基本参数
首先计算波长 λ \lambda λ,
λ
=
c
f
=
3
×
10
8
12.5
×
10
9
=
0.024
m
=
24
mm
\begin{aligned} \lambda &= \frac{c}{f} \\[5pt] &= \frac{3 \times 10^8}{12.5 \times 10^9} \\[5pt] &= 0.024\,\text{m} = 24\,\text{mm} \end{aligned}
λ=fc=12.5×1093×108=0.024m=24mm
因此,阵元间距
d
=
λ
2
=
12
mm
d = \frac{\lambda}{2} = 12\,\text{mm}
d=2λ=12mm。
第二步,建立物理模型与理论公式
要让波束偏转 40 ∘ 40^\circ 40∘,其物理本质是,通过调控相邻阵元之间的信号相位差,使得阵元辐射的信号在指定方向实现同相叠加。相邻阵元间的固定相位差 Δ ϕ \Delta \phi Δϕ 计算公式为,
$
\Delta \phi = \frac{2\pi}{\lambda} \cdot d \cdot \sin\theta
$
由于 d = λ 2 d = \frac{\lambda}{2} d=2λ,代入上式可得简化的相位差公式,
$
\Delta \phi = \pi \cdot \sin\theta
$
第三步,代入数值进行计算
计算
sin
40
∘
≈
0.6428
\sin 40^\circ \approx 0.6428
sin40∘≈0.6428。
则相邻阵元的相位差
Δ
ϕ
=
180
∘
×
0.6428
≈
115.7
∘
\Delta \phi = 180^\circ \times 0.6428 \approx 115.7^\circ
Δϕ=180∘×0.6428≈115.7∘。
假设第1个阵元的初始相位为 0 ∘ 0^\circ 0∘,则后续阵元的相位依次累加此相位差。
- 阵元 1, 0 ∘ 0^\circ 0∘
- 阵元 2, 115.7 ∘ 115.7^\circ 115.7∘
- 阵元 3,
231.4
∘
231.4^\circ
231.4∘
… 以此类推。
为便于硬件实现,通常会将相位归一化到 0 ∘ 0^\circ 0∘ 至 360 ∘ 360^\circ 360∘ 范围内。
| 阵元编号 | 理论相位(度) | 归一化相位( 0 ∼ 360 ∘ 0\sim360^\circ 0∼360∘) |
|---|---|---|
| 1 | 0 | 0.0 |
| 2 | 115.7 | 115.7 |
| 3 | 231.4 | 231.4 |
| 4 | 347.1 | 347.1 |
| 5 | 462.8 | 102.8 |
| 6 | 578.5 | 218.5 |
| 7 | 694.2 | 334.2 |
| 8 | 809.9 | 89.9 |
3. 二维相控阵天线移相器相位计算
现实中的相控阵天线通常是二维面阵。这里,我们以一个 8 × 8 8 \times 8 8×8 的二维面阵,共 64 个阵元,为例进行说明。
场景设定
- 工作频率, 12.5 GHz 12.5\,\text{GHz} 12.5GHz。
- 阵元分布, 8 × 8 8 \times 8 8×8,水平和垂直方向的阵元间距均为 λ 2 \frac{\lambda}{2} 2λ。
- 期望指向角, 方位角
α
=
15
∘
\alpha = 15^\circ
α=15∘,俯仰角
E
l
=
60
∘
El = 60^\circ
El=60∘。
- 注意,在相控阵计算中,我们通常使用离轴角 θ \theta θ。离轴角, θ \theta θ,即波束指向与天线法线方向的夹角,可由俯仰角, E l El El,通常指与地平线的夹角,转换得到, θ = 90 ∘ − E l = 30 ∘ \theta = 90^\circ - El = 30^\circ θ=90∘−El=30∘。
计算公式
对于二维阵列中位于第 m m m 行,第 n n n 列的阵元,其相位 Φ m , n \Phi_{m,n} Φm,n 的通用计算公式为,
Φ
m
,
n
=
2
π
λ
⋅
d
⋅
[
(
m
−
1
)
sin
θ
cos
α
+
(
n
−
1
)
sin
θ
sin
α
]
\begin{aligned} \Phi_{m,n} &= \frac{2\pi}{\lambda} \cdot d \cdot \left[ (m-1)\sin\theta\cos\alpha + (n-1)\sin\theta\sin\alpha \right] \end{aligned}
Φm,n=λ2π⋅d⋅[(m−1)sinθcosα+(n−1)sinθsinα]
同样,代入
d
=
λ
2
d = \frac{\lambda}{2}
d=2λ,公式可简化为,
Φ m , n = π ⋅ [ ( m − 1 ) sin θ cos α + ( n − 1 ) sin θ sin α ] \begin{aligned} \Phi_{m,n} &= \pi \cdot \left[ (m-1)\sin\theta\cos\alpha + (n-1)\sin\theta\sin\alpha \right] \end{aligned} Φm,n=π⋅[(m−1)sinθcosα+(n−1)sinθsinα]
带入数值计算
- sin θ = sin 30 ∘ = 0.5 \sin\theta = \sin 30^\circ = 0.5 sinθ=sin30∘=0.5
- cos α = cos 15 ∘ ≈ 0.9659 \cos\alpha = \cos 15^\circ \approx 0.9659 cosα=cos15∘≈0.9659
- sin α = sin 15 ∘ ≈ 0.2588 \sin\alpha = \sin 15^\circ \approx 0.2588 sinα=sin15∘≈0.2588
基于此,我们可以计算出两个方向上的固定相位差。
- 行方向相位差 Δ Φ x \Delta \Phi_x ΔΦx, 180 ∘ × 0.5 × 0.9659 ≈ 86.9 ∘ 180^\circ \times 0.5 \times 0.9659 \approx 86.9^\circ 180∘×0.5×0.9659≈86.9∘
- 列方向相位差 Δ Φ y \Delta \Phi_y ΔΦy, 180 ∘ × 0.5 × 0.2588 ≈ 23.3 ∘ 180^\circ \times 0.5 \times 0.2588 \approx 23.3^\circ 180∘×0.5×0.2588≈23.3∘
假设左上角第一个阵元
(
1
,
1
)
(1,1)
(1,1) 的相位为
0
∘
0^\circ
0∘。
那么,阵元
(
2
,
1
)
(2,1)
(2,1) 的相位即为
Δ
Φ
x
=
86.9
∘
\Delta \Phi_x = 86.9^\circ
ΔΦx=86.9∘。
阵元
(
1
,
2
)
(1,2)
(1,2) 的相位为
Δ
Φ
y
=
23.3
∘
\Delta \Phi_y = 23.3^\circ
ΔΦy=23.3∘。
阵元
(
2
,
2
)
(2,2)
(2,2) 的相位则为
Δ
Φ
x
+
Δ
Φ
y
=
86.9
∘
+
23.3
∘
=
110.2
∘
\Delta \Phi_x + \Delta \Phi_y = 86.9^\circ + 23.3^\circ = 110.2^\circ
ΔΦx+ΔΦy=86.9∘+23.3∘=110.2∘。
由于64个数据较多,此处列出前10个阵元归一化后的相位值以供参考。
| 阵元位置 ( m , n ) (m, n) (m,n) | 理论相位(度,归一化) |
|---|---|
| (1, 1) | 0.0 |
| (1, 2) | 23.3 |
| (1, 3) | 46.6 |
| (1, 4) | 69.9 |
| (2, 1) | 86.9 |
| (2, 2) | 110.2 |
| (2, 3) | 133.5 |
| (2, 4) | 156.8 |
| (3, 1) | 173.8 |
| (3, 2) | 197.1 |
由此可得,通过精确控制这64个阵元的相位,我们就能使天线的波束精确指向预设的方位角与俯仰角。
4.总结
本文系统地解答了如何从波束指向角度计算出每个移相器所需相位的核心问题。关键点总结如下,
- 理论基础,无论是一维线阵还是二维面阵,其核心原理都是通过控制各阵元间的相对相位差,使电磁波在目标方向实现相干叠加。
- 核心公式,相邻阵元的相位差主要由工作波长,阵元间距和期望指向角的正弦值共同决定,其通用表达式为 Δ ϕ = 2 π λ ⋅ d ⋅ sin θ \Delta \phi = \frac{2\pi}{\lambda} \cdot d \cdot \sin\theta Δϕ=λ2π⋅d⋅sinθ。
- 工程实践,在 12.5 GHz 12.5\,\text{GHz} 12.5GHz 的高频下,微小的物理尺寸偏差都会导致显著的相位误差。因此,天线在出厂前的幅相一致性标定是保证其性能至关重要的环节。
然而,上述计算得到的均为理论上的连续相位值。实际的工程实现中,移相器存在位数限制,我们采用数控移相器。这便引出了新的问题,在位数限制下,移相器的实际量化相位值是多少,由此带来的量化误差如何,最终导致的波束指向误差有多大,以及这些误差将如何影响天线的整体发射或接收性能。
我们将在后续文章中详细介绍这些工程实践中的量化影响。
如果你对天线系统性能指标G/T值的估算感兴趣,可以先参阅我之前发布的这篇文章:《卫星通信接收天线G/T值速查表》。文中提供了详细的计算小程序,可帮助您快速进行等效口径反算。
码字不易,大家觉得文章不错,就安排一下一键三连吧:点赞、分享、推荐。
“通信与导航”公众号主页有技术文章的分类合集,感兴趣的朋友可以查询。




















 1245
1245

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








