T型三电平变流器FCS-MPC算法优化【附代码】

✅ 博主简介：擅长数据搜集与处理、建模仿真、程序设计、仿真代码、论文写作与指导，毕业论文、期刊论文经验交流。

 ✅成品或者定制，扫描文章底部微信二维码。

---

（1）基于新型扇区寻优和电容充电平衡的FCS-MPC优化算法

T型三相三电平变流器在运行过程中能够输出二十七种不同的开关状态组合，这些开关状态对应着空间矢量平面内的十九个基本电压矢量。传统有限控制集模型预测控制算法在每个采样周期内需要对全部二十七种开关状态进行遍历计算，通过代价函数评估每种状态的优劣程度，最终选取代价函数值最小的开关状态作为下一采样周期的控制输入。这种全遍历的计算方式虽然能够确保找到全局最优解，但其计算复杂度随着电平数的增加呈指数级增长，在实际工程应用中对控制器的运算能力提出了极高的要求。此外，传统算法的代价函数通常包含电流跟踪误差项和中点电位平衡项，两个优化目标之间需要通过权重因子进行协调，而权重因子的选取往往依赖于工程经验和大量的试验调试，缺乏系统化的设计方法。

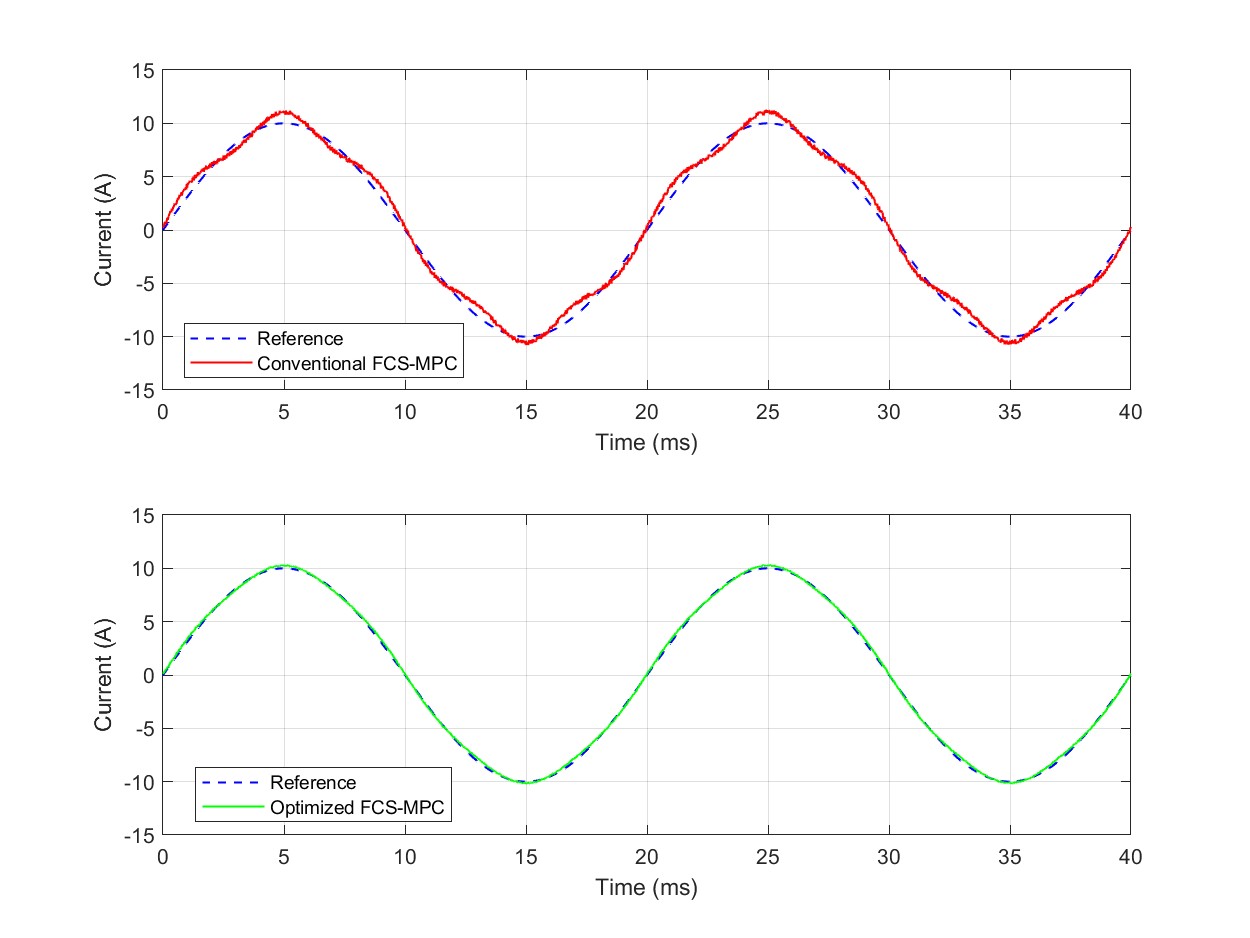
针对上述问题，本研究提出了一种基于新型扇区寻优策略的FCS-MPC优化算法。该算法的核心思想是利用参考电压矢量的空间位置信息来预先筛选候选开关状态，从而大幅降低需要遍历计算的状态数量。具体而言，空间矢量平面被划分为六个大扇区，每个大扇区又被进一步细分为四个小扇区，形成总共二十四个小扇区的精细划分结构。在每个采样周期开始时，算法首先根据参考电压矢量的幅值和相角判断其所处的小扇区位置，然后仅对该小扇区及其相邻小扇区内的电压矢量进行代价函数评估。通过这种扇区预筛选机制，需要遍历的候选状态数量从二十七种减少到六至八种，算法的计算复杂度降低了约百分之七十。

扇区判断的准确性是保证优化算法性能的关键因素。本研究设计了一种基于坐标变换的快速扇区定位方法，该方法首先将三相参考电压通过克拉克变换转换为两相静止坐标系下的电压分量，然后通过比较这两个分量的大小关系和符号特征来确定参考矢量所在的大扇区编号。在确定大扇区后，进一步利用参考矢量幅值与预设阈值的比较结果来判断其所处的小扇区位置。整个扇区判断过程仅涉及简单的比较运算和逻辑判断，不需要三角函数计算，因此具有极高的执行效率。为了应对参考矢量位于扇区边界附近时可能出现的判断误差，算法在边界区域引入了适当的滞回机制，通过设置判断阈值的上下边界来避免频繁的扇区切换现象。

电容中点电位平衡是T型三电平变流器控制中的另一核心问题。直流侧两个串联电容的电压在理想情况下应该保持相等，但由于负载不对称、器件参数偏差等因素的影响，实际运行中两个电容电压往往会出现偏差。中点电位偏移不仅会导致输出电压波形畸变，还可能造成功率器件承受过高的电压应力，影响系统的安全稳定运行。传统FCS-MPC算法通过在代价函数中添加中点电位偏差惩罚项来实现平衡控制，但这种方法需要通过权重因子来协调电流跟踪和中点平衡两个优化目标，权重因子的选取缺乏明确的理论指导。

本研究提出了一种基于电容充电状态的中点电位平衡策略，该策略无需引入权重因子即可实现电流跟踪和中点平衡的协同优化。策略的基本原理是根据当前电容电压偏差的方向和大小，在候选电压矢量中优先选择具有适当中点电流方向的矢量。具体实现时，算法首先检测两个电容的电压值并计算其偏差，然后根据偏差极性确定期望的中点电流方向。在对候选矢量进行评估时，算法计算每个矢量对应的中点电流值，并将中点电流方向与期望方向一致的矢量标记为优先选择对象。当存在多个满足电流跟踪要求且中点电流方向正确的候选矢量时，算法选择中点电流幅值与期望值最接近的矢量作为最终输出。

为了进一步提高中点电位平衡的动态响应速度，本研究还设计了分级控制机制。当电容电压偏差小于预设的第一阈值时，中点平衡控制处于低优先级状态，此时算法主要关注电流跟踪性能；当偏差超过第一阈值但小于第二阈值时，中点平衡控制进入中优先级状态，算法在保证基本电流跟踪性能的前提下加强中点平衡调节；当偏差超过第二阈值时，中点平衡控制上升到高优先级状态，算法将中点平衡作为首要优化目标，必要时可以牺牲部分电流跟踪精度。这种分级控制机制能够在正常运行和扰动恢复两种工况下都保持良好的控制性能，避免了固定权重因子方法在不同工况下性能差异较大的问题。

算法的软件实现采用模块化设计思想，将扇区判断、候选矢量筛选、代价函数计算、中点平衡控制等功能封装为独立的子模块，各模块之间通过标准化的数据接口进行通信。这种设计方式不仅便于算法的调试和维护，还为后续的功能扩展预留了充足的空间。在实际应用中，算法的主控制周期被划分为采样、计算和输出三个阶段，其中采样阶段完成电流和电压的数据采集，计算阶段执行预测模型计算和优化决策，输出阶段将选定的开关状态发送到驱动电路。通过合理安排各阶段的执行时序和优化关键代码的运行效率，算法的总体执行时间相比传统全遍历方法减少了约十六微秒，完全满足高开关频率应用场合的实时性要求。

（2）基于零序分量注入和矢量合成的FCS-MPC优化算法

传统有限控制集模型预测控制算法直接将离散的开关状态作为控制输出，每个采样周期内仅施加一个电压矢量，这种控制方式虽然实现简单但存在明显的局限性。首先，由于电压矢量的离散性，输出电压只能在有限的矢量位置之间跳变，无法实现对参考矢量的精确逼近，导致稳态电流纹波较大，特别是在低调制度和低频运行工况下控制精度显著下降。其次，开关状态的切换完全由代价函数的优化结果决定，缺乏对开关频率的直接控制能力，不同运行工况下的开关频率波动较大，给电磁兼容设计和滤波器设计带来困难。此外，电流谐波在频谱上呈现分散分布的特征，不利于通过滤波器进行有效抑制。

针对上述问题，本研究提出了一种基于零序分量注入和矢量合成的FCS-MPC优化算法，该算法在保持模型预测控制快速动态响应优势的同时，引入空间矢量调制的思想来改善稳态性能。算法的核心创新点是在预测控制框架内实现对合成矢量的精确计算和对开关序列的优化安排，从而同时达到固定开关频率、降低电流谐波和保持中点电位平衡的多重目标。

零序分量注入是提高三电平变流器调制性能的有效手段。在三相三线制系统中，零序电压分量不会在负载中产生零序电流，因此可以在不影响输出线电压的前提下对相电压波形进行调整。本研究采用的零序分量注入策略是将三相参考电压的最大值和最小值进行适当的线性组合，得到需要注入的零序电压值。这种方法的优点是计算简单且能够自动适应不同的调制度和功率因数工况，注入零序分量后的调制波具有更好的对称性，能够有效减小输出电流的谐波含量。更重要的是，零序分量的注入使得三相调制波的峰值被压缩，直流电压利用率得到提高，在相同直流母线电压条件下可以输出更高的交流电压幅值。

矢量合成是本算法实现高控制精度的关键技术。与传统FCS-MPC每个周期只能输出单一矢量不同，本算法在每个采样周期内合成一个等效电压矢量，该等效矢量由多个基本矢量按照特定的时间比例组合而成。矢量合成的基本原理是利用伏秒平衡原则，通过控制各基本矢量的作用时间来调节它们的加权平均值，使等效矢量能够精确指向参考矢量的位置。具体实现时，算法首先根据参考矢量的位置确定构成合成矢量的基本矢量组合，通常选择参考矢量所在三角形的三个顶点矢量；然后根据伏秒平衡方程计算各基本矢量的作用时间；最后按照优化的开关序列将各矢量依次施加到变流器。

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

class TTypeThreeLevelConverter:
    def __init__(self, vdc=400, fs=10000, l_filter=3e-3, r_filter=0.1):
        self.vdc = vdc
        self.fs = fs
        self.ts = 1.0 / fs
        self.l_filter = l_filter
        self.r_filter = r_filter
        self.c_dc = 2200e-6
        self.voltage_vectors = self._generate_voltage_vectors()
        self.sector_table = self._build_sector_table()
        
    def _generate_voltage_vectors(self):
        vectors = {}
        states = [-1, 0, 1]
        idx = 0
        for sa in states:
            for sb in states:
                for sc in states:
                    va = sa * self.vdc / 2
                    vb = sb * self.vdc / 2
                    vc = sc * self.vdc / 2
                    v_alpha = (2*va - vb - vc) / 3
                    v_beta = (vb - vc) / np.sqrt(3)
                    vectors[idx] = {'state': (sa, sb, sc), 'alpha': v_alpha, 'beta': v_beta}
                    idx += 1
        return vectors
    
    def _build_sector_table(self):
        sector_vectors = {i: [] for i in range(24)}
        for idx, vec in self.voltage_vectors.items():
            angle = np.arctan2(vec['beta'], vec['alpha'])
            if angle < 0:
                angle += 2 * np.pi
            mag = np.sqrt(vec['alpha']**2 + vec['beta']**2)
            sector = int(angle / (np.pi / 12)) % 24
            sector_vectors[sector].append(idx)
        return sector_vectors
    
    def determine_sector(self, v_ref_alpha, v_ref_beta):
        angle = np.arctan2(v_ref_beta, v_ref_alpha)
        if angle < 0:
            angle += 2 * np.pi
        sector = int(angle / (np.pi / 12)) % 24
        return sector

class FCSMPC:
    def __init__(self, converter, prediction_horizon=1):
        self.converter = converter
        self.horizon = prediction_horizon
        self.lambda_np = 0.5
        self.vc1 = converter.vdc / 2
        self.vc2 = converter.vdc / 2
        
    def predict_current(self, i_current, v_applied, v_grid, dt):
        di = (v_applied - v_grid - self.converter.r_filter * i_current) / self.converter.l_filter
        i_next = i_current + di * dt
        return i_next
    
    def cost_function(self, i_pred_alpha, i_pred_beta, i_ref_alpha, i_ref_beta, np_deviation):
        current_error = (i_pred_alpha - i_ref_alpha)**2 + (i_pred_beta - i_ref_beta)**2
        np_cost = self.lambda_np * np_deviation**2
        return current_error + np_cost
    
    def calculate_np_current(self, state, i_a, i_b, i_c):
        sa, sb, sc = state
        i_np = 0
        if sa == 0:
            i_np += i_a
        if sb == 0:
            i_np += i_b
        if sc == 0:
            i_np += i_c
        return i_np

class OptimizedFCSMPC(FCSMPC):
    def __init__(self, converter):
        super().__init__(converter)
        self.candidate_reduction_enabled = True
        
    def get_candidate_vectors(self, sector):
        candidates = set()
        for s in range((sector - 1) % 24, (sector + 2) % 24):
            candidates.update(self.converter.sector_table.get(s % 24, []))
        candidates.add(0)
        candidates.add(13)
        return list(candidates)
    
    def select_optimal_vector(self, i_alpha, i_beta, i_ref_alpha, i_ref_beta, v_grid_alpha, v_grid_beta, sector):
        candidates = self.get_candidate_vectors(sector)
        min_cost = float('inf')
        optimal_idx = 0
        np_deviation = self.vc1 - self.vc2
        for idx in candidates:
            vec = self.converter.voltage_vectors[idx]
            i_pred_alpha = self.predict_current(i_alpha, vec['alpha'], v_grid_alpha, self.converter.ts)
            i_pred_beta = self.predict_current(i_beta, vec['beta'], v_grid_beta, self.converter.ts)
            cost = self.cost_function(i_pred_alpha, i_pred_beta, i_ref_alpha, i_ref_beta, np_deviation)
            if cost < min_cost:
                min_cost = cost
                optimal_idx = idx
        return optimal_idx

class VectorSynthesisFCSMPC(FCSMPC):
    def __init__(self, converter, switching_freq=10000):
        super().__init__(converter)
        self.fsw = switching_freq
        self.tsw = 1.0 / switching_freq
        
    def inject_zero_sequence(self, va_ref, vb_ref, vc_ref):
        v_max = max(va_ref, vb_ref, vc_ref)
        v_min = min(va_ref, vb_ref, vc_ref)
        v_zero = -0.5 * (v_max + v_min)
        return va_ref + v_zero, vb_ref + v_zero, vc_ref + v_zero
    
    def calculate_duty_cycles(self, v_ref_alpha, v_ref_beta, sector):
        angle = sector * np.pi / 12
        v1_alpha = self.converter.vdc / 2 * np.cos(angle)
        v1_beta = self.converter.vdc / 2 * np.sin(angle)
        v2_alpha = self.converter.vdc / 2 * np.cos(angle + np.pi / 6)
        v2_beta = self.converter.vdc / 2 * np.sin(angle + np.pi / 6)
        det = v1_alpha * v2_beta - v2_alpha * v1_beta
        if abs(det) < 1e-10:
            return 0, 0, 1.0
        d1 = (v_ref_alpha * v2_beta - v_ref_beta * v2_alpha) / det
        d2 = (v1_alpha * v_ref_beta - v1_beta * v_ref_alpha) / det
        d0 = 1.0 - d1 - d2
        d1 = np.clip(d1, 0, 1)
        d2 = np.clip(d2, 0, 1)
        d0 = np.clip(d0, 0, 1)
        total = d1 + d2 + d0
        if total > 0:
            d1 /= total
            d2 /= total
            d0 /= total
        return d1, d2, d0
    
    def generate_switching_sequence(self, d1, d2, d0, sector):
        sequence = []
        t_total = self.tsw
        t0 = d0 * t_total / 4
        t1 = d1 * t_total / 2
        t2 = d2 * t_total / 2
        sequence.append(('V0', t0))
        sequence.append(('V1', t1))
        sequence.append(('V2', t2))
        sequence.append(('V7', t0 * 2))
        sequence.append(('V2', t2))
        sequence.append(('V1', t1))
        sequence.append(('V0', t0))
        return sequence
    
    def balance_neutral_point(self, d_positive, d_negative, np_error):
        kp = 0.1
        adjustment = kp * np_error
        d_positive_new = d_positive - adjustment
        d_negative_new = d_negative + adjustment
        d_positive_new = np.clip(d_positive_new, 0, 1)
        d_negative_new = np.clip(d_negative_new, 0, 1)
        return d_positive_new, d_negative_new

def simulate_converter(controller, duration=0.1, f_fundamental=50):
    t = np.arange(0, duration, controller.converter.ts)
    n_steps = len(t)
    i_alpha = np.zeros(n_steps)
    i_beta = np.zeros(n_steps)
    v_out_alpha = np.zeros(n_steps)
    v_out_beta = np.zeros(n_steps)
    vc1_history = np.zeros(n_steps)
    vc2_history = np.zeros(n_steps)
    i_ref_mag = 10.0
    omega = 2 * np.pi * f_fundamental
    for k in range(1, n_steps):
        i_ref_alpha = i_ref_mag * np.cos(omega * t[k])
        i_ref_beta = i_ref_mag * np.sin(omega * t[k])
        v_grid_alpha = 0
        v_grid_beta = 0
        sector = controller.converter.determine_sector(i_ref_alpha * 10, i_ref_beta * 10)
        if isinstance(controller, VectorSynthesisFCSMPC):
            d1, d2, d0 = controller.calculate_duty_cycles(i_ref_alpha * 20, i_ref_beta * 20, sector)
            np_error = controller.vc1 - controller.vc2
            d1, d2 = controller.balance_neutral_point(d1, d2, np_error)
            v_out_alpha[k] = d1 * controller.converter.vdc / 2
            v_out_beta[k] = d2 * controller.converter.vdc / 2
        else:
            opt_idx = controller.select_optimal_vector(i_alpha[k-1], i_beta[k-1], i_ref_alpha, i_ref_beta, v_grid_alpha, v_grid_beta, sector)
            vec = controller.converter.voltage_vectors[opt_idx]
            v_out_alpha[k] = vec['alpha']
            v_out_beta[k] = vec['beta']
        i_alpha[k] = controller.predict_current(i_alpha[k-1], v_out_alpha[k], v_grid_alpha, controller.converter.ts)
        i_beta[k] = controller.predict_current(i_beta[k-1], v_out_beta[k], v_grid_beta, controller.converter.ts)
        vc1_history[k] = controller.vc1
        vc2_history[k] = controller.vc2
    return t, i_alpha, i_beta, v_out_alpha, v_out_beta, vc1_history, vc2_history

def calculate_thd(signal_data, fs, fundamental_freq):
    n = len(signal_data)
    fft_result = np.fft.fft(signal_data)
    freq = np.fft.fftfreq(n, 1/fs)
    magnitude = np.abs(fft_result) / n
    fund_idx = np.argmin(np.abs(freq - fundamental_freq))
    fund_mag = magnitude[fund_idx] * 2
    harmonic_power = 0
    for h in range(2, 51):
        h_freq = h * fundamental_freq
        h_idx = np.argmin(np.abs(freq - h_freq))
        harmonic_power += (magnitude[h_idx] * 2) ** 2
    thd = np.sqrt(harmonic_power) / fund_mag * 100 if fund_mag > 0 else 0
    return thd

if __name__ == "__main__":
    converter = TTypeThreeLevelConverter(vdc=400, fs=20000, l_filter=3e-3, r_filter=0.1)
    standard_mpc = OptimizedFCSMPC(converter)
    vector_synth_mpc = VectorSynthesisFCSMPC(converter, switching_freq=10000)
    t1, ia1, ib1, va1, vb1, vc1_1, vc2_1 = simulate_converter(standard_mpc, duration=0.05)
    t2, ia2, ib2, va2, vb2, vc1_2, vc2_2 = simulate_converter(vector_synth_mpc, duration=0.05)
    thd1 = calculate_thd(ia1[1000:], converter.fs, 50)
    thd2 = calculate_thd(ia2[1000:], converter.fs, 50)
    print(f"Standard Optimized FCS-MPC THD: {thd1:.2f}%")
    print(f"Vector Synthesis FCS-MPC THD: {thd2:.2f}%")
    print(f"THD Reduction: {thd1 - thd2:.2f}%")

 

成品代码50-200，定制300起，可以直接沟通

👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇