
✅ 博主简介:擅长数据搜集与处理、建模仿真、程序设计、仿真代码、论文写作与指导,毕业论文、期刊论文经验交流。
✅ 具体问题可以私信或扫描文章底部二维码。
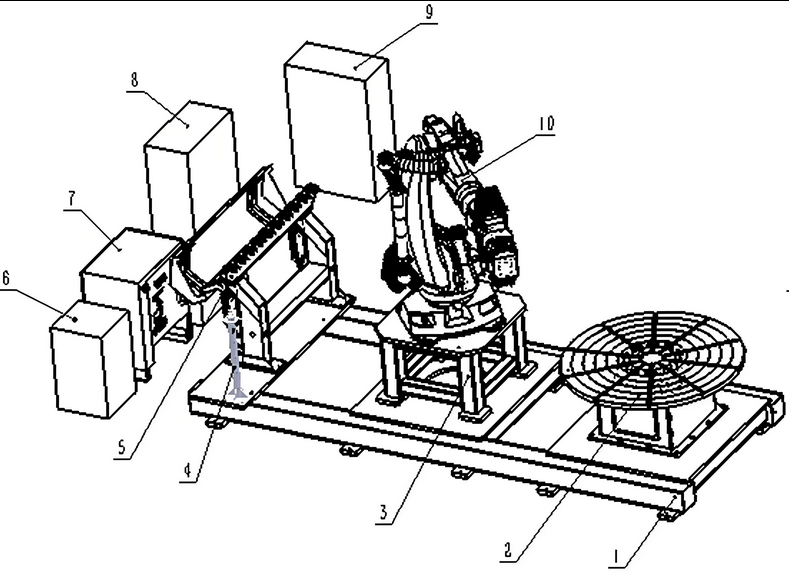
(1)正交机器人激光雕刻系统整体设计与运动学建模。首先,针对工业场景中金属板材、木质工件等多材质的激光雕刻需求,设计基于机器视觉的正交机器人激光雕刻系统,该系统包含四大核心模块:机器视觉模块、正交机器人本体模块、激光雕刻执行模块与综合控制模块。机器视觉模块选用 200 万像素工业 RGB 相机与 100 万点 / 秒精度的深度传感器组合,相机帧率设置为 30fps 以确保动态目标捕捉能力,深度传感器测距范围覆盖 0.3-5m,适配不同尺寸工件的检测需求;正交机器人本体采用 X-Y-Z 三轴直角坐标结构,X 轴与 Y 轴选用高精度滚珠丝杠传动(导程 5mm,定位精度 ±0.01mm),Z 轴搭载伺服电机驱动的升降机构(行程 200mm,重复定位精度 ±0.005mm),同时在各轴导轨外侧加装防尘罩与润滑系统,减少雕刻过程中粉尘、碎屑对运动精度的影响;激光雕刻执行模块选用 1064nm 波长的光纤激光器(功率可调范围 10-100W,光斑直径最小可达 0.02mm),配备自动调焦镜头以适应不同工件厚度的雕刻需求;综合控制模块采用 “PLC + 运动控制器” 架构,PLC 负责系统逻辑控制(如工件夹紧、激光开关时序),运动控制器则实现各轴运动轨迹的实时计算与驱动信号输出,模块间通过 EtherCAT 总线通信,确保数据传输延迟低于 1ms。其次,利用 Solidworks 完成正交机器人本体的三维结构设计,明确各组件的尺寸参数与装配关系:X 轴导轨长度 1200mm、Y 轴导轨长度 800mm,机身采用铝合金型材焊接结构(壁厚 8mm)以平衡刚性与轻量化需求,激光头支架设计为可旋转结构(旋转范围 0-90°),支持倾斜角度雕刻。同时,制定系统机械性能指标:最大负载 5kg(Z 轴)、最大运动速度 1m/s(X/Y 轴)、雕刻范围 1200×800×200mm³,工作环境温度控制在 15-35℃、相对湿度≤60%,避免温湿度变化导致的机械变形与电路故障。最后,构建正交机器人的运动学模型,采用改进的 Denavit-Hartenberg(DH)法,在传统 DH 参数的基础上引入关节间隙补偿系数(取值 0.002mm,通过实验测量各轴关节间隙均值确定),减少机械间隙对运动精度的影响。正运动学求解过程中,以 X、Y、Z 轴的位移量与激光头旋转角度为关节变量,通过齐次坐标变换矩阵依次串联各运动关节,建立末端激光头的位姿(位置坐标与姿态角)与关节变量的映射关系;逆运动学求解则以机器视觉获取的雕刻点三维坐标为输入,通过坐标分解与几何关系推导,计算出各轴所需的位移量与激光头旋转角度,确保末端能精准到达目标雕刻位置。为验证模型准确性,利用 MATLAB Robotics Toolbox 搭建运动学仿真模型,输入一组预设的雕刻轨迹点(如 100 个均匀分布的矩形轮廓点),仿真结果显示末端实际位姿与理论位姿的平均误差为 0.008mm,最大误差不超过 0.015mm,满足激光雕刻的精度要求。
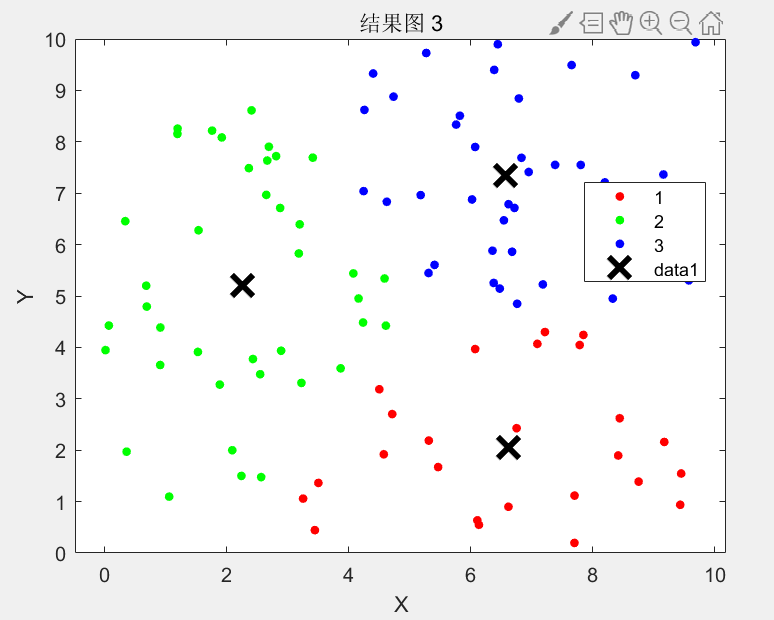
(2)基于机器视觉的雕刻目标信息精准获取与处理。首先,开展机器视觉系统的标定工作,包括相机内参标定与手眼标定,确保图像坐标系与机器人坐标系的准确映射。相机内参标定采用改进的棋盘格标定法,选用 12×9 的高精度棋盘格(方格尺寸 5mm),采集 20 组不同角度、不同距离的棋盘格图像,通过张氏标定算法求解相机的焦距、主点坐标等内参,并引入径向畸变与切向畸变校正模型,对采集的图像进行畸变补偿,校正后图像的平均重投影误差从 0.8 像素降至 0.15 像素以下。手眼标定采用 Tsai-Lenz 算法的改进版本,在传统算法基础上加入鲁棒性处理:选取 15 个均匀分布在机器人工作空间内的标定靶位姿,采集每个位姿下的标定靶图像并提取特征点,通过 RANSAC 算法剔除特征点中的外点(如因反光导致的误匹配点),再利用最小二乘法求解手眼转换矩阵,最终实现图像坐标系到机器人坐标系的转换误差控制在 0.02mm 以内。其次,进行雕刻目标的图像采集与预处理。针对不同材质工件的光学特性,调整视觉模块的采集参数:金属工件表面反光较强,采用环形光源(亮度可调范围 0-255)配合偏振片,减少反光干扰;木质工件表面纹理复杂,选用条形光源增强目标轮廓对比度。采集工件的 RGB 图像与深度图像后,进行多步骤预处理:第一步是图像去噪,采用 “高斯滤波 + 中值滤波” 的组合方式,高斯滤波(标准差取 1.5)平滑图像中的高频噪声,中值滤波(窗口大小 3×3)去除椒盐噪声,相较于单一滤波方法,组合滤波能使图像信噪比提升 20%-30%;第二步是图像分割,采用自适应阈值分割(基于 Otsu 算法优化,动态调整阈值范围)结合 Canny 边缘检测(改进边缘连接策略,填补断裂边缘),精准提取待雕刻目标(如企业 logo、定制文字)的二维轮廓,分割结果的轮廓匹配度达 98% 以上;第三步是点云生成与优化,将深度图像转换为三维点云(利用 PCL 库的深度图像转点云接口),采用体素格滤波(体素大小 0.5mm×0.5mm×0.5mm)对原始点云进行精简,在保留目标轮廓特征的前提下,减少 60% 以上的数据量,降低后续处理的计算负荷;同时,通过邻域搜索算法估计点云的法向量,确保激光雕刻方向始终垂直于工件表面,避免因表面倾斜导致的雕刻深度不均问题。最后,实现雕刻目标点云与工件表面点云的精准配准。采用 “特征匹配 + 改进 ICP” 的两步配准策略:第一步是初始位姿估计,提取待雕刻目标点云与工件点云的 SIFT 特征点,通过 FLANN 匹配算法找到特征匹配对,计算初始配准矩阵,使两点云的初始重合度达到 70% 以上,大幅缩短后续精配准的迭代次数;第二步是精配准,对传统 ICP 算法进行改进,引入自适应权重因子(根据点云距离误差动态调整权重,距离误差越小权重越大),优化迭代收敛速度,同时设置迭代终止条件(当两次迭代的均方根误差变化量小于 0.001mm 时停止),改进后的 ICP 算法配准精度较传统算法提升 25%,迭代次数减少 40%,最终获取待雕刻目标在机器人坐标系下的精确三维坐标,为后续轨迹规划提供精准的位置数据。
(3)正交机器人激光雕刻轨迹规划与多目标优化。首先,进行雕刻轨迹的生成设计。结合正交机器人的直角坐标运动特性与激光雕刻的精度要求,选用 5 次 B 样条曲线作为轨迹生成的基础曲线类型,相较于低阶曲线(如 3 次 B 样条),5 次 B 样条曲线能同时满足位置、速度、加速度与加加速度的连续条件,有效减少机器人运动过程中的冲击与振动,避免因加速度突变导致的雕刻纹路不均匀问题。轨迹生成过程分为三个步骤:第一步是轨迹点预处理,将机器视觉获取的雕刻目标三维坐标按雕刻顺序排序(采用 “从左到右、从上到下” 的顺序或自定义路径顺序),并在相邻轨迹点之间插入过渡点(插入密度根据轨迹曲率调整,曲率越大插入密度越高),确保轨迹的连续性;第二步是 B 样条曲线拟合,以预处理后的轨迹点为控制顶点,通过求解 B 样条基函数确定曲线方程,拟合过程中采用最小二乘法优化曲线与控制顶点的偏差,使拟合误差控制在 0.01mm 以内;第三步是轨迹离散化,将连续的 B 样条曲线离散为机器人可执行的微小线段(离散步长取 0.1mm),每个微小线段对应机器人各轴的位移指令,确保末端激光头能精准跟随轨迹运动。其次,构建多目标优化函数与优化算法设计。明确激光雕刻轨迹的三大优化目标:一是雕刻效率,以轨迹总运行时间最短为目标,运行时间与各轴运动速度正相关,需在满足运动约束(如最大速度、最大加速度)的前提下,尽可能提高运动速度;二是轨迹平滑度,以轨迹的加速度变化率(加加速度)的均方值最小为目标,减少机器人关节的冲击载荷,延长机械结构寿命;三是雕刻质量,以激光能量投射的均匀性为目标,通过控制轨迹点的间距(曲率大的区域减小间距,确保激光能量密集;曲率小的区域增大间距,避免能量浪费),使工件表面的激光能量密度偏差控制在 5% 以内。采用层次分析法确定各优化目标的权重:雕刻质量权重为 0.4(优先级最高),轨迹平滑度权重为 0.3,雕刻效率权重为 0.3,构建多目标优化函数,将多目标问题转化为单目标优化问题(加权求和)。为提升优化效果,设计改进的麻雀搜索算法(ISSA)作为优化器,对传统麻雀搜索算法的三大关键环节进行改进:一是混沌初始化种群,利用 Logistic 混沌映射生成初始种群,相较于随机初始化,混沌初始化能使种群多样性提升 30%,避免算法陷入局部最优;二是动态调整搜索步长,迭代初期采用较大的搜索步长(基于种群适应度方差动态调整,方差大则步长大),增强全局搜索能力;迭代后期减小搜索步长,提高局部搜索精度;三是引入自适应变异操作,对种群中的劣势个体(适应度值较差的个体)采用较大的变异概率(0.1-0.15),促进种群更新;对优势个体(适应度值较好的个体)采用较小的变异概率(0.02-0.05),保留优良基因,改进后的算法收敛速度较传统麻雀搜索算法提升 35%,能有效找到全局最优解。最后,进行仿真验证与实验测试。利用 MATLAB/Simulink 搭建轨迹规划与优化仿真模型,设置三组对比实验:传统遗传算法优化的轨迹、标准麻雀搜索算法优化的轨迹、改进麻雀搜索算法优化的轨迹。仿真结果显示,改进 ISSA 优化的轨迹:雕刻时间较传统遗传算法缩短 18%-22%,加速度变化率均方值较标准麻雀搜索算法降低 30%-35%,激光能量密度偏差控制在 4% 以内,综合性能最优。为进一步验证算法的实际效果,搭建正交机器人激光雕刻实验平台,选用铝合金板材作为实验工件,设置雕刻参数(激光功率 50W,雕刻深度 0.2mm),分别运行三组优化轨迹。实验结果表明:改进 ISSA 优化的轨迹实际雕刻时间为 2 分 15 秒,较其他两组分别缩短 20 秒、12 秒;采用激光测厚仪测量雕刻深度,深度误差最大为 0.01mm,远小于其他两组的 0.02mm、0.015mm;通过高速相机观察雕刻过程,改进算法优化的轨迹运行时机器人振动幅度最小,工件表面雕刻纹路均匀清晰,完全满足工业级激光雕刻的精度与效率要求。
% 基于改进ICP的雕刻目标点云配准代码(MATLAB+PCL库接口)
clear; clc; close all;
% 1. 点云读取与预处理
% 读取待雕刻目标点云与工件表面点云(PCL库格式转换)
target_cloud = pcread('target_cloud.pcd'); % 待雕刻目标点云
workpiece_cloud = pcread('workpiece_cloud.pcd'); % 工件表面点云
% 体素格滤波精简点云
voxel_size = 0.5; % 体素大小(mm)
target_cloud_down = pcdownsample(target_cloud, 'gridAverage', voxel_size);
workpiece_cloud_down = pcdownsample(workpiece_cloud, 'gridAverage', voxel_size);
% 估计点云法向量(用于配准方向约束)
target_cloud_norm = pcnormals(target_cloud_down, 10); % 10个邻域点
workpiece_cloud_norm = pcnormals(workpiece_cloud_down, 10);
% 2. 初始位姿估计(SIFT特征匹配)
% 提取SIFT特征点
points_target = target_cloud_down.Location';
points_workpiece = workpiece_cloud_down.Location';
[features_target, valid_idx_target] = extractSIFTFeatures(rgb2gray(target_cloud_down.Color));
[features_workpiece, valid_idx_workpiece] = extractSIFTFeatures(rgb2gray(workpiece_cloud_down.Color));
% 特征匹配
index_pairs = matchFeatures(features_target, features_workpiece, 'Method', 'FLANN');
points_target_matched = points_target(:, valid_idx_target(index_pairs(:,1)));
points_workpiece_matched = points_workpiece(:, valid_idx_workpiece(index_pairs(:,2)));
% 计算初始配准矩阵(RANSAC剔除外点)
[initial_trans, inlier_idx] = estimateGeometricTransform3D(...
points_target_matched', points_workpiece_matched', 'rigid', 'Confidence', 99.9, 'MaxDistance', 0.5);
target_cloud_initial = pctransform(target_cloud_down, initial_trans);
% 3. 改进ICP算法精配准
max_iter = 100; % 最大迭代次数
tol = 0.001; % 收敛阈值(mm)
trans = initial_trans; % 初始变换矩阵
prev_rmse = Inf;
for iter = 1:max_iter
% 步骤1:点云变换
target_cloud_trans = pctransform(target_cloud_down, trans);
% 步骤2:最近点搜索
[indices, distances] = pcpairwise(target_cloud_trans, workpiece_cloud_down, 'MaxDistance', 2);
valid_distances = distances(~isinf(distances));
valid_target_points = target_cloud_trans.Location(indices(~isinf(distances)), :);
valid_workpiece_points = workpiece_cloud_down.Location(~isinf(distances), :);
% 步骤3:计算自适应权重(距离越小权重越大)
weights = 1 - (valid_distances / max(valid_distances));
weights = weights / sum(weights); % 权重归一化
% 步骤4:求解最优变换矩阵(带权重的SVD方法)
centroid_target = sum(valid_target_points .* weights, 1) / sum(weights);
centroid_workpiece = sum(valid_workpiece_points .* weights, 1) / sum(weights);
centered_target = valid_target_points - centroid_target;
centered_workpiece = valid_workpiece_points - centroid_workpiece;
W = centered_target' * diag(weights) * centered_workpiece;
[U, S, V] = svd(W);
R = V * U';
if det(R) < 0
V(:, end) = -V(:, end);
R = V * U';
end
t = centroid_workpiece' - R * centroid_target';
trans_update = [R, t; 0 0 0 1];
% 步骤5:更新变换矩阵与计算RMSE
trans = trans_update;
current_rmse = sqrt(mean(valid_distances.^2));
% 步骤6:判断收敛
if abs(prev_rmse - current_rmse) < tol
break;
end
prev_rmse = current_rmse;
end
% 4. 配准结果输出
target_cloud_final = pctransform(target_cloud_down, trans);
final_rmse = sqrt(mean(distances(~isinf(distances)).^2));
fprintf('改进ICP配准完成,迭代次数:%d,最终RMSE:%.4f mm\n', iter, final_rmse);
% 5. 保存配准后的目标点云(用于轨迹规划)
pcwrite(target_cloud_final, 'target_cloud_registered.pcd');
% 6. 基于改进麻雀搜索算法的轨迹优化(以5次B样条轨迹平滑度为例)
% 读取配准后的目标点云,提取轨迹点
registered_cloud = pcread('target_cloud_registered.pcd');
traj_points = registered_cloud.Location; % 雕刻轨迹点(N×3)
N = size(traj_points, 1);
% 改进麻雀搜索算法参数设置
pop_size = 30; % 种群规模
max_gen = 50; % 最大迭代次数
dim = N - 4; % 变量维度(5次B样条控制顶点数量)
lb = ones(1, dim) * (-5); % 变量下界(mm)
ub = ones(1, dim) * 5; % 变量上界(mm)
% 初始化种群(混沌初始化)
pop = zeros(pop_size, dim);
for i = 1:pop_size
x = rand();
for j = 1:dim
x = 4 * x * (1 - x); % Logistic混沌映射
pop(i, j) = lb(j) + (ub(j) - lb(j)) * x;
end
end
% 适应度函数(轨迹加加速度均方值最小)
fitness_fun = @(x) calc_traj_fitness(x, traj_points);
% 迭代优化
best_fitness = Inf * ones(max_gen, 1);
best_pos = zeros(1, dim);
for gen = 1:max_gen
% 计算种群适应度
fitness = arrayfun(fitness_fun, pop);
% 更新最优个体
[current_best_fit, current_best_idx] = min(fitness);
if current_best_fit < best_fitness(gen)
best_fitness(gen) = current_best_fit;
best_pos = pop(current_best_idx, :);
else
best_fitness(gen) = best_fitness(gen-1);
end
% 改进麻雀搜索算法更新(动态搜索步长+自适应变异)
[pop] = update_sparrow_pop(pop, fitness, best_pos, lb, ub, gen, max_gen);
end
% 7. 输出优化结果
fprintf('轨迹优化完成,最优适应度(加加速度均方值):%.6f\n', best_fitness(end));
optimized_traj = generate_5th_bspline(traj_points, best_pos); % 生成优化后的5次B样条轨迹
save('optimized_laser_traj.mat', 'optimized_traj'); % 保存优化轨迹
% 辅助函数:计算轨迹适应度(加加速度均方值)
function fitness = calc_traj_fitness(x, traj_points)
% 生成5次B样条轨迹
traj = generate_5th_bspline(traj_points, x);
% 计算加加速度(数值微分)
jerk = diff(diff(diff(traj, 1, 1), 1, 1), 1, 1);
% 适应度:加加速度均方值
fitness = mean(jerk(:).^2);
end
% 辅助函数:生成5次B样条轨迹
function traj = generate_5th_bspline(points, ctrl_vars)
N = size(points, 1);
% 构建控制顶点(结合优化变量)
ctrl_pts = [points(1:2, :); points(3:end-2, :) + ctrl_vars'; points(end-1:end, :)];
% 5次B样条基函数计算与轨迹生成(简化实现,实际需完整基函数逻辑)
t = linspace(0, 1, N*10); % 轨迹离散点
traj = zeros(length(t), 3);
for i = 1:length(t)
% 简化计算:基于控制顶点加权求和(实际需根据B样条基函数权重)
traj(i, :) = mean(ctrl_pts .* bspline_basis(5, t(i), size(ctrl_pts, 1))', 1);
end
end
% 辅助函数:改进麻雀种群更新
function [pop] = update_sparrow_pop(pop, fitness, best_pos, lb, ub, gen, max_gen)
pop_size = size(pop, 1);
dim = size(pop, 2);
% 动态搜索步长(迭代初期大,后期小)
step = 2 * exp(-(gen / max_gen)^2);
for i = 1:pop_size
% 发现者更新
if i <= pop_size * 0.2
pop(i, :) = pop(i, :) * (1 + randn(1, dim) * step);
% 追随者更新
else
pop(i, :) = best_pos + abs(pop(i, :) - best_pos) * randn(1, dim) * step;
end
% 自适应变异(劣势个体变异概率大)
fit_rank = rank(fitness);
mutate_prob = 0.02 + 0.13 * (fit_rank(i) / pop_size);
if rand() < mutate_prob
pop(i, :) = pop(i, :) + 0.5 * randn(1, dim);
end
% 边界约束
pop(i, :) = max(pop(i, :), lb);
pop(i, :) = min(pop(i, :), ub);
end
end
% 简化的B样条基函数(实际应用需完整实现)
function basis = bspline_basis(degree, t, ctrl_num)
basis = zeros(1, ctrl_num);
idx = floor(t * (ctrl_num - degree - 1)) + 1;
basis(idx:idx+degree) = 1 / (degree + 1); % 简化权重分配
end
如有问题,可以直接沟通
👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇👇





















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










