3D数基础：图形与游戏开发一书重要知识点概要

最近在看《3D数基础：图形与游戏开发》，这篇博文只是大致记录一下书中的重点知识点，后面会对每一个重点都写一篇专门的博文来详细介绍。本文还在持续更新中......

第二章：

左右手坐标系，unity使用左手坐标系，3D MAX使用右手坐标系

第三章：坐标系

惯性坐标系

在物体坐标系与世界坐标系中，引入了一个惯性坐标系，惯性坐标系的原点与物体坐标系的原点重合，惯性坐标系的轴平行于世界坐标系的轴，所以物体坐标系到世界坐标系的转换可以通过：1.先旋转到惯性坐标系；2.再平移到世界坐标系；来实现。

定位物体在世界中的位置

定位物体的某一个点，只需要知道物体原点（由美工决定）到某一点相对位置，再看世界坐标系到物体原点的相对位置，即可计算出某一点在世界坐标系中的位置（同一方向坐标系可通过旋转得到）如果某一物体没有出现在视野中，就不用把每一个点的位置算出，只需要追踪到原点的位置即可。

嵌套坐标系

在世界坐标系中追踪某个复杂物体每一个部分的位置变动是非常困难的，因此，我们使用嵌套坐标系，举个例子，人在走动的时候，人的手在人体坐标系中只是绕某一个轴摆动的，人的双腿也是如此，人的头发也只是在Y轴或者Z轴上做改变，而如果把这些坐标的计算全部放到世界坐标系中，那计算量就太大了。（人坐标系相对于人头坐标系，就相当于世界坐标系相对于人坐标系）

嵌套坐标系也能在虚拟世界的坐标系中动态的更新，比如，头发从人头上落下来，头发的坐标系就从人头坐标系变成了世界坐标系。

总之，嵌套坐标系只是为了以最方便的方式描述物体。

第四章：向量

第五章：向量运算

零向量、负向量、向量大小（长度或者模）；

向量不能乘另一个向量、向量的标准化（向量除以他的模，零向量不能被标准化）；

向量的加法满足交换律，向量的减法不满足交换律；

距离公式；

点乘（内积，cos）的几何意义、用途（比如可以变换点乘公式来求投影的长度、求两向量的方向、夹角，另外，零向量和其他所有向量的点乘结果都为0，对此的几何解释是，0向量和其他所有向量都垂直）；

叉乘（外积，||axb||=||a||x||b||sin(a,b)），叉乘和点乘在一起的时候，叉乘优先运算，因为点乘的结果是一个标量，而标量和向量不能叉乘，叉积可以用来求面积和法向量；

叉积的方向：在一个垂直于你目光的平面上，可以通过把两个向量首尾相接（axb，则把a的头和b的尾相接），看是顺时针还是逆时针，在左手坐标系中，如果是顺时针，则指向你，如果是逆时针，则远离你；

运算a·(bxc)称作三重积，特殊的性质在第九章记录；

线性代数公式可以复习一下；

计算平行于某一向量的分量和垂直于某一向量的分量；

第六章：3D向量类

3D向量类的C++实现；

只实现用到最多的方法，只重载必要的运算符；

不要为2%的性能提升100%的代码复杂度；

第七章：矩阵

方阵、单位阵、转置、对角矩阵（所有非对角线元素为0），矩阵乘法（不满足交换律、满足结合律）

线性变换

本书基本使用行向量，少数必要的地方用列向量（如用向量来和矩阵连接）

行向量的话可以直接左乘：vABC，列向量则要右乘：CBAv；

第八章：矩阵和线性变换

变换物体与变换坐标系，要根据实际的情况来取舍；（有时变换坐标系会方便一点，如旋转物体的话需要旋转这个复杂物体上所有的定点，那这个时候我们就可以选择旋转坐标系）

二维坐标系绕原点变换的变换矩阵

左手坐标系的顺时针旋转（指从坐标轴的正端看向负端）是正方向，右手坐标系的顺时针旋转是负方向；

旋转公式指的是物体在原坐标系中的坐标的变化，而不是在新坐标系中的位置

绕X轴顺时针（左手坐标系，正方向）旋转的公式为：

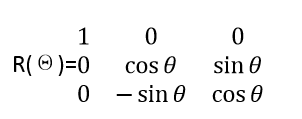
绕其他轴旋转的公式也可参考得知，绕任意轴旋转也一样（比较复杂）

缩放、投影、镜像，其实是一个东西（投影：缩放因子为0，镜像：缩放因子为-1）

切变（把某个坐标乘以若干个系数，然后加到其他轴上去，比如xy的坐标被z轴改变，就是把z轴乘上系数a、b，x轴被系数a乘上z轴所改变，y轴被系数b乘上z轴所改变，记作Hxy），切变后，物体的面积、体积不变。

几种重要的变换：见表8.8.7

第九章：矩阵的更多知识

行列式，行列式的性质（积的行列式等于行列式的积，可扩展到多个矩阵的情况）、行列式的几何解释（类似于叉积，只不过带符号，表示正向还是负向），行列式的计算（利用代数余子式，或者选择主元）

余子式（矩阵），代数余子式（值，标量）

矩阵的逆（标准伴随矩阵除原矩阵的行列式），可用于反向计算或者撤销上一步计算

正交矩阵，正交矩阵的转置矩阵和逆矩阵相等，所以如果是正交矩阵，就不用计算逆矩阵，直接用转置矩阵即可；

矩阵的正交化（施密特算法）

4x4矩阵

因为3x3矩阵只能表示线性变换，为了方便计算引入了4x4矩阵；4x4矩阵提供了一种方便表示向量变化的方法，即用第四维表示平移，所以我们可以用4x4矩阵表示线性和非线性的变换，常用的有：平移，透视投影

本文还在持续更新中......