[LC] 338. Counting Bits

最新推荐文章于 2024-06-17 23:08:18 发布

Daisy么么哒

最新推荐文章于 2024-06-17 23:08:18 发布

阅读量163

点赞数

CC 4.0 BY-SA版权

分类专栏： Leetcode

本文链接：https://blog.youkuaiyun.com/chaochen1407/article/details/97623483

Leetcode 专栏收录该内容

294 篇文章

订阅专栏

本文探讨了一种使用位运算结合动态规划的高效算法，用于计算一系列整数的二进制表示中1的个数。通过观察数字的二进制模式，发现规律并应用动态规划思想，实现了比传统逐个计数更优的时间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

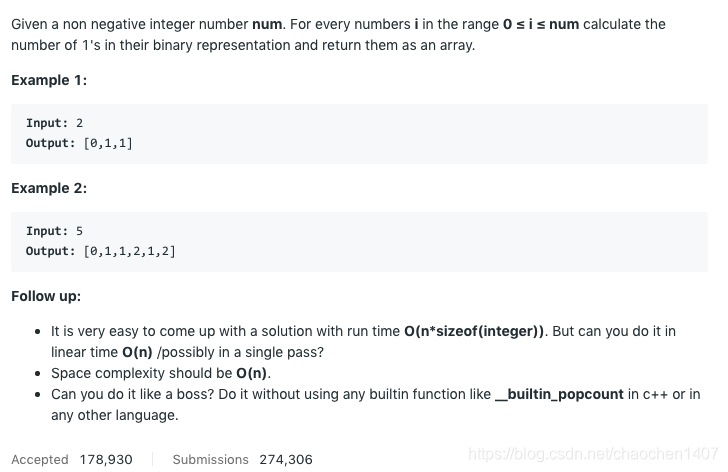
先来个简单版本的答案，就是对每个数字进行bit count。count的方法已经很烂大街了，就不阐述了。

    public int[] countBits(int num) {
        int[] result = new int[num + 1];
        for (int i = 0; i <= num; i++) {
            result[i] = this.countIntBits(i);
        }
        
        return result;
    }
    
    public int countIntBits(int num) {
        int res = 0;
        while (num != 0) {
            num &= num - 1;
            res++;
        }
        
        return res;
    }

这个就是所谓的O(n * sizeofinteger)的答案了吧。这个还是能过判定的。

然后高级版答案是咋样的呢。思考了很久，突破点应该是DP，其实也思考到了大概方向，然后，我就懒得想了。于是参考了一下各种答案，得出（摘抄得）以下最优解。

其实原理并不复杂。下面看几组数字就能看出来规律了。

0 ~ 1: 0, 1
2 ~ 3: 10, 11
4 ~ 7: 100, 101, 110, 111
8 ~ 15 : 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111

所以说，0和1是这次dp的base cases。然后在大于1的数字里，有着如下规律

[2 ^ 1 ~ 2 ^ 2) : f(i) = f(i - 2^1) + 1 (这个加的1就是二进制里最前面的那个1)
[2 ^ 2 ~ 2 ^ 3) : f(i) = f(i - 2 ^ 2) + 1 (同上。就是4 ～ 7 其实就是 0 ～ 3的二进制前面加个1，也就是十进制的4）
[2 ^ 3 ~ 2 ^ 4) : f(i) = f(i - 2 ^ 3) + 1 (同理， 8 ~ 15其实就是0 ~ 7的二进制前面加个1，也就是十进制的8)

所以，其实
[2 ^ n ~ 2 ^ (n + 1)) : f(i) = f(i - 2 ^ n) + 1

根据上面的算法，其实只需要在遍历 0 ~ num的时候判断自己在哪个区间然后套用上面公式即可。。给出代码如下：

    public int[] countBits(int num) {
        int[] result = new int[num + 1];
        int curBitPos = 1;
        int nextBitPos = 2;
        for (int i = 1; i <= num; i++) {
            if (nextBitPos == i) {
                curBitPos = nextBitPos;
                nextBitPos *= 2;
            }
            
            result[i] = result[i - curBitPos] + 1;
        }
        
        return result;
    }