[Leetcode]276. Paint Fence

最新推荐文章于 2019-06-03 14:12:21 发布

原创最新推荐文章于 2019-06-03 14:12:21 发布 · 666 阅读

0 ·

CC 4.0 BY-SA版权

Leetcode 专栏收录该内容

294 篇文章

订阅专栏

博客围绕一道有明显动态规划（dp）特征的题目展开。该题递推关系在于n和n - 2，探讨了递推式的形成，考虑当前fence与之前颜色不同和相同两种情况，得出递推式f(n) = f(n - 1) * (k - 1) + f(n - 2) * (k - 1)，还提及两个base case，最后表示可据此得到代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

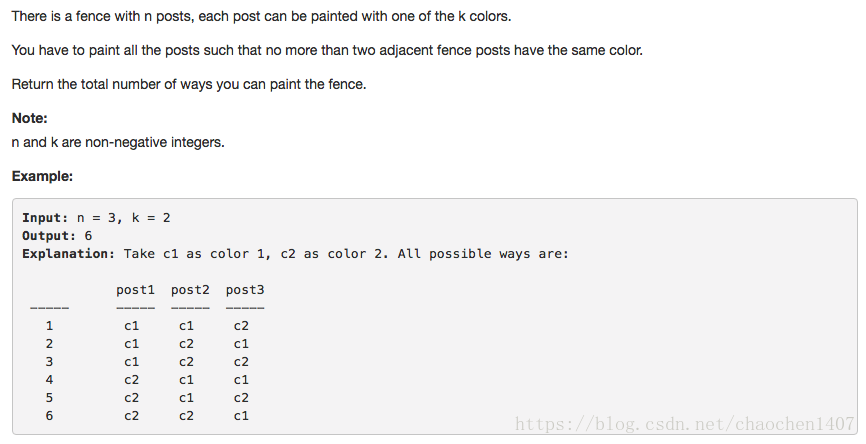
这题虽然是easy题，但其实，我个人还是不是特别的明白。所以还是记录一下

这题其实还是有很明显的dp特征的，只是这一题的限制或者说关系并不在于n和n - 1，而是在于n和n - 2。也就是前一面fence是怎么样并不直接影响当前这一堵fence。

先探讨一下这个递推式是怎么形成的。
只有两种情况需要考虑，首先是当前的fence和之前的fence颜色不同。如果说之前的fence颜色的总数是f(n - 1)，不同的情况表示你还有k - 1种颜色可以选择
那么总数的第一部分是f(n) = f(n - 1) * (k - 1) + ???
总数的另一部分就是和上一个fence颜色相同的情况。仔细观察不难发现其实如果这一个fence和上一个fence颜色相同的情况，其数目应该是上一个fence和上上个fence颜色不同的数目，也就是f(n - 2) * (k - 1)，因为不能出现连续三个fence相同的情况。
所以其实递推式就是f(n) = f(n - 1) * (k - 1) + f(n - 2) * (k - 1)
同时，这个递推式是有两个base case的，就是f(1) = k， f(2) = k * k，所以递推是从n = 3开始的。

根据以上推理，可以得到代码如下：

    public int numWays(int n, int k) {
        if (n == 0) return 0;
        if (n == 1) return k;
        int prev = k * k, pPrev = k, res = prev;
        for (int i = 3; i <= n; i++) {
            res = prev * (k - 1) + pPrev * (k - 1);
            pPrev = prev;
            prev = res;
        }

        return res;
    }