密度聚类

引言

其实对于所有的聚类问题，都有一个核心点，那就是以什么样的规则来划分两个点是不是同一类。密度聚类，本质上就是基于一种密度的概念来进行聚类。而密度的定义本质上也是来自于两点的距离，所以其实对于聚类的算法来看，大家本质上都差不多，谁也别笑话谁。下面我们来总结介绍一种叫做DBSCAN的密度算法。

DBSCAN

DBSCAN 的全称是 Density-Based Spatial Clustering of Applications with Noise
单词里面有个noise,这就说明我们的算法是能抗噪声的，并且我们的算法是可以在空间中聚类为任意形状的聚类的，这点是一些其他的聚类算法不具备的性质，如下所示：

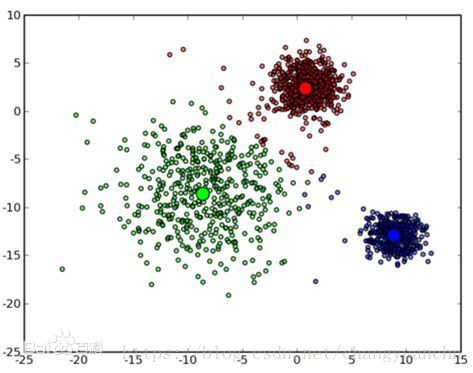
具有这样的性能，就是因为我们的算法引入了“邻域”（其参数为$(\varepsilon, MinPts )$）的概念来刻画样本的紧密程度的算法。

下面我们来介绍一下这个算法，在具体算法之前，我们先看几个定义，非常简单，但是可能比较绕，懂了这几个定义，下面的算法就是小菜一碟了。

基于密度的几个概念

$\varepsilon -$邻域：

对$x_j \in D$，其$\varepsilon -$邻域是指样本集$D$中与$x_j$距离不大于$\varepsilon$的样本，即$N_{\varepsilon}(x_j) = \left \{ x_j \in D | dist(x_i,x_j) \leq \varepsilon \right \}$

核心对象：

对象$x_j$的$\varepsilon -$邻域中至少包含$MinPts$个样本，即$N_{\varepsilon}(x_j) \geq MinPts$，则称$x_j$为核心对象。

密度直达：

若$x_j$位于$x_i$的$\varepsilon -$邻域中，且$x_i$是核心对象，则称$x_j$由$x_i$密度直达。

密度可达：

对$x_j$与$x_i$，存在样本序列$p_1,p_2,...,p_n$且$p_1 = x_j , p_n = x_i$ 且$p_{i+1}$由$p_{i}$密度直达，则称$x_j$由$x_i$密度可达。

其实这个概念本质上要求$p_2,...,p_n$都是核心对象

密度相连：

对$x_j$与$x_i$，若存在$x_k$使得$x_j$与$x_i$均由$x_k$密度可达，则称$x_j$由$x_i$密度相连。

下图直观的表示了这几个概念

基于上面的概念，可以定义DBSCAN算法里面的簇的定义

簇： 由密度可达关系导出的最大的密度相连的样本集合。

因此实际上簇$C \subseteq D$满足下面的两个条件：

连接性：$x_i \in C,x_j \in C \Rightarrow$ $x_i$与$x_j$密度相连

最大性：$x_i \in C$ 且$x_j$由$x_i$密度可达 $\Rightarrow x_j \in C$

实际上就是核心对象以及与其密度可达的所有的点的集合

本质上相当于一些核心对象以及边界点组成了簇，簇中核心的点就是核心对象。

具体算法描述

实际上就是核心对象以及与其密度可达的所有的点的集合

输入

• 样本集 $D = \left \{ x_1,...,x_N \right \}$
• 邻域参数$(\varepsilon, MinPts )$

算法流程

• 
  
• 找出所有的核心对象，放入集合中 $\Omega$
• 初始化未访问的样本集合：$\Gamma = D$
• $while( \Omega \neq \varnothing)$
  

• 
  
• $\Gamma_{old} = D$
  
• 随机选取一个核心对象$o \in \Omega$，初始化$Q = <o>$
  
• $\Gamma = \Gamma \setminus \left \{ o \right \}$
  
• $while( Q \neq \varnothing)$
  

• 
  
• 从 $Q$中取出样本$q$
  
• $if (q$是核心对象$)$
  

• 另$\Delta = N_{\varepsilon}(q) \cap \Gamma$， 即获取核心对象$q$邻域内的点
  
• 将$\Delta$内的点加入到$Q$中
  
• $\Gamma = \Gamma \setminus \Delta$
  
• $end \quad if$
  
• $end \quad while$
  
• $k = k+1$,并且生成聚类簇$C_k = \Gamma_{old} \setminus \Gamma$
  
• $\Omega = \Omega \setminus C_k$
• $end \quad while$

输出

簇划分$C = \left \{ C_1,...,C_K \right \}$

算法的优缺点

优点：

• 算法不需要指定聚类的数目，但是算法实际上需要另外两个参数$(\varepsilon, MinPts )$，所以这个优点也是勉强。
• 可以聚成任意形状的类，就像开始的图所示
• 能够识别出噪声点

缺点：

• 对高维数据效果不算好
• 如果样本的密度不均， 效果会不理想